


Las plantas que crecen en este bosque son superficies orientables y no orientables. Toda superficie orientable, sin frontera y compacta, se puede obtener de una esfera pegándole algún número de "asas" y deformándola, por ejemplo:


La supeficie no orientable más conocida es la banda de Moebius:
Su frontera es un círculo. De las superficies no orientables sin frontera, probablemente, la más famosa es la botella de Klein:
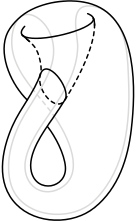
La botella de Klein no se puede realizar en el espacio tridimensional sin autointersecciones.
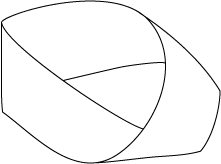
Sin embargo, la superficie no orientable más fundamental, en cierto sentido, es el llamado plano proyectivo. Se obtiene de un disco al identificar los puntos opuestos de su frontera, o (lo que es lo mismo), de un cuadrado, cuando se identifican los lados opuestos en direcciones contrarias:

Tampoco puede realizarse en el espacio tridimensional sin autointersecciones. El plano proyectivo se puede visualizar de la siguiente manera:

En la parte de la derecha del dibujo, se muestran las secciones del plano proyectivo con planos horizontales en $\mathbb{R}^3$.
Resulta que cada superficie no orientable se puede obtener de la esfera haciendo cierto número de agujeros e identificando los puntos opuestos en el borde de cada agujero:
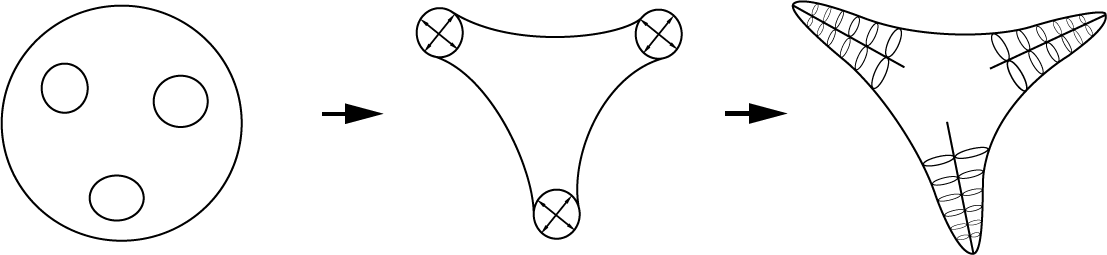
Estos agujeros con los puntos opuestos identificados son los "helechos" en el dibujo de Fomenko.
