

Esta es la tercera parte de nuestro trabajo sobre “El Baúl de Problemas” de la Miscelánea Matemática. Como en la segunda entrega, resolveremos primeramente los problemas que se plantearon en la ocasión anterior. Presentaremos después una nueva lista de problemas para el deleite de los asiduos lectores de universo.math. Una vez más, los problemas que sean planteados en esta ocasión aparecerán próximamente en El irracional y las soluciones más atractivas que en dicho sitio se recaben serán consideradas para ser incluidas en la siguiente entrega de este trabajo. ¡Están todos invitados a participar en los threads que sobre estos problemas se abrirán en El irracional!
A continuación presentamos soluciones y comentarios para los cinco problemas planteados en el número anterior. Entre estos se encuentran los problemas 9, 10 y 11 de “El Baúl de Problemas”. Cuando una solución se basa en ideas aportadas a El irracional, se mencionará de manera explícita en el texto. Hemos puesto un * en aquellos problemas para los que presentamos algunos comentarios adicionales que podrían resultar interesantes para los lectores.
En el tema que se abrió en el El irracional para este problema, Malors Emilio Espinosa Lara mencionó que, al tenerse que
\[\{10^n\varphi-\flo{10^{n}\varphi} \,:\, n \in \mathbb{N}\} \subseteq \{n\varphi-\flo{n\varphi} \,:\, n \in \mathbb{N}\},\]sólo hacía falta demostrar la afirmación en el inciso $\mathrm{b})$ del problema. La demostración que Malors Espinosa ofrece para $\mathrm{b})$ puede formularse de la siguiente manera:
Para establecer que el conjunto $\mathcal{F}=\{10^n\varphi-\flo{10^{n}\varphi}\,:\, n \in \mathbb{N}\}$ es denso, basta ver que para cualquier $x\in[0,1]$ existe una sucesión conformada por elementos de $\mathcal{F}$ que converge a $x$. Supongamos que la representación en base $10$ de $x$ es $\sum_{j=1}^\infty \frac{a_j}{10^j}$ con $a_j\in\{0,1,\ldots,9\}$. Notemos que $10^n\varphi-\flo{10^n\varphi}$ es el número que se obtiene al iniciar $\varphi$ en la $n$-ésima cifra después del punto decimal. Como en $\varphi$ aparecen todos los números enteros positivos, uno tras otro, entonces si se elige $n \in \mathbb{N}$ de manera adecuada podemos hacer que $10^n\varphi-\flo{10^n\varphi}$ empiece con cualquier conjunto ordenado de dígitos que queramos. Así, para cada $n \in \mathbb{N}$ existe $m_n \in \mathbb{N}$ tal que
\[ 10^{m_n}\varphi-\flo{10^{m_n}\varphi}=\sum_{j=1}^n \frac{a_j}{10^j}+\epsilon_n \]donde $\epsilon_n \in (0,\frac{1}{10^n})$, pues el número $10^{m_n}\varphi-\flo{10^{m_n}\varphi}$ difiere de $x$ sólo a partir de la $(n+1)$-ésima cifra después del punto decimal. Al tenerse que $\epsilon_n\to 0$, se sigue que
\begin{eqnarray*} \lim_{n\to \infty} (10^{m_n}\varphi-\flo{10^{m_n}\varphi})=x \end{eqnarray*}y la demostración termina.
▢
Al número irracional $0.123456789101112\ldots$ se le conoce como la constante de Champernowne. La manera más simple de establecer la irracionalidad de la constante de Champernowne es aplicando este criterio: si $\{a_{n}\}_{n \in \mathbb{N}}$ es una sucesión estrictamente creciente de números naturales, la serie $\sum_{n=1}^{\infty} \frac{1}{a_{n}}$ es divergente y $\alpha \in \mathbb{R}$ se obtiene al yuxtaponer, después del punto decimal, los términos consecutivos de la sucesión $\{a_{n}\}_{n \in \mathbb{N}}$, entonces $\alpha \in \mathbb{R}\setminus \mathbb{Q}$ (una demostración de este sencillo criterio puede encontrarse en [1J. Hernández, Más sobre Erdös. En internet: http://elr3to.blogspot.mx/2011/08/mas-sobre-erdos.html ], [4N. Hegyvári, On some irrational decimal fractions. Amer. Math. Monthly Vol. 100, 8, Oct. 1993, pp. 779-780. , pp. 779-780] o [5D. J. Newman, R. Breusch y F. Herzog, Solution to problem 4494. Amer. Math. Monthly Vol. 60, 9, Nov. 1953, pp. 632-633. , pp. 632-633]).
Es menester añadir que el aserto en el inciso a) es válido para cualquier número irracional $\varphi$, no sólo para la constante de Champernowne.
Cualquier función polinomial de grado a lo más $2$ satisface la ecuación funcional dada. En efecto, si $a, b$ y $c$ son números reales fijos y $f(x) = ax^{2}+bx+c$ para cada $x \in \mathbb{R}$ entonces
\begin{eqnarray*} \frac{f(y)-f(x)}{y-x} &=& \frac{a(y^{2}-x^{2})+b(y-x)}{y-x}\\ &=& a(y+x) + b\\ &=& f^{\prime}\left(\frac{x+y}{2}\right) \end{eqnarray*}siempre que $x$ y $y$ son números reales diferentes.
Omar Antolín Camarena demostró en El irracional que una función diferenciable $f \colon \mathbb{R}\to\mathbb{R}$ que satisface la ecuación funcional $(\ref{ecf})$ es necesariamente una función polinomial de grado a lo más $2$. Esto lo estableció como sigue.
La expresión en el lado derecho de $(\ref{ecf})$ es el valor promedio de la función $f^{\prime}$ en el intervalo $[x,y]$ pues
\[\frac{f(y)-f(x)}{y-x} = \frac{1}{y-x} \int_{x}^{y} f^{\prime}(t) \, dt.\]De esto se desprende que si $f$ satisface la ecuación funcional $(\ref{ecf})$ entonces $f^{\prime} \colon \mathbb{R} \to \mathbb{R}$ es una función diferenciable y, además, para cualesquiera $x, y \in \mathbb{R}$ con $x \lt y$, el valor promedio de $f^{\prime}$ en el intervalo $[x,y]$ es igual al valor que $f^{\prime}$ toma en el punto medio de $[x,y]$.
Lo anterior equivale a decir que $f^{\prime}$ es una función armónica (cf. [9E. M. Stein y R. Shakarchi, Real Analysis (Measure Theory, Integration, & Hilbert Spaces). Princeton University Press, Princeton NJ, USA, 2005, p. 235., Teorema 4.2]). Puesto que las funciones armónicas de una variable son las funciones polinomiales de grado a lo más $1$, concluimos que $f$ es efectivamente una función polinomial de grado a lo más $2$.
▢
En la figura que aparece a continuación, los puntos $D$, $E$, $F$, $G$, $H$ e $I$ son los extremos de las prolongaciones que se están considerando. En consecuencia, estos puntos son tales que $\overline{AD}=\overline{AE}=\overline{BC}$, $\overline{BF}=\overline{BG}=\overline{CA}$ y $\overline{CH}=\overline{CI}=\overline{AB}$.
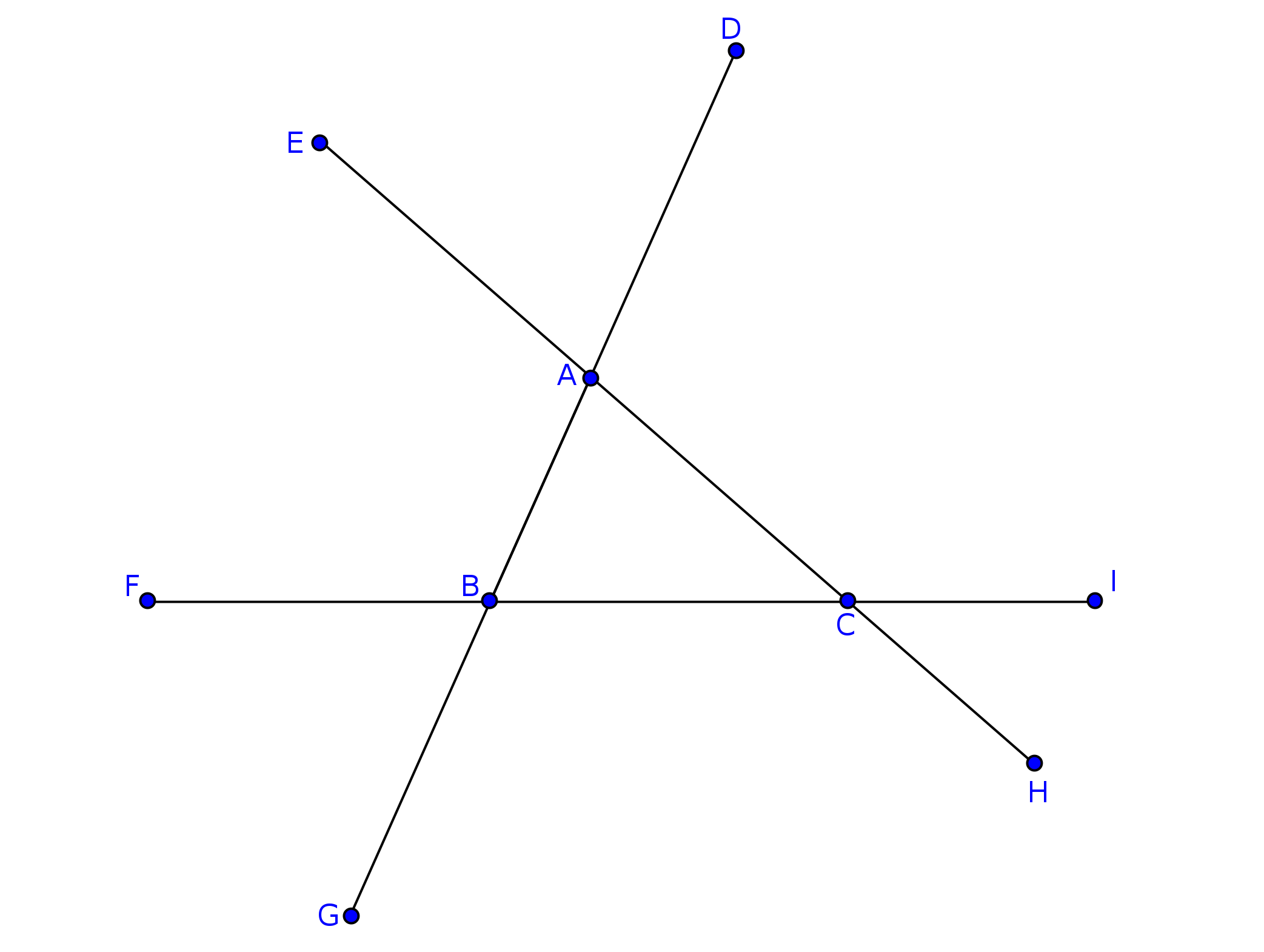
Puesto que los triángulos $ADE$, $BFG$ y $CHI$ son isósceles se sigue que $\angle ADE = \angle DEA =: \alpha$, $\angle BFG = \angle FGB =: \beta$ y $\angle CHI = \angle HIC =: \gamma$. Por otro lado, al tenerse que $\overline{AG}= \overline{AH}$ y que $\angle DAE = \angle GAH$ (por ser ángulos opuestos por el vértice) se obtiene que $\triangle DAE \sim \triangle GAH$ y por consiguiente, $\angle AGH = \angle AHG = \alpha$. Procediendo de manera análoga puede establecerse que $\angle BDI = \angle BID = \beta$ y $\angle CEF = \angle CFE = \gamma$. En vista de todo esto se tiene que
\begin{eqnarray*} \angle DEF + \angle FID &=& (\angle DEA+ \angle AEF)+\angle BID\\ &=& \angle DEA + \angle CEF + \angle BID\\ &=& \alpha + \gamma + \beta\\ &=& \frac{180^{\circ}-\angle CAB}{2} + \frac{180^{\circ}-\angle BCA}{2} + \frac{180^{\circ}-\angle ABC}{2}\\ &=& 180^{\circ} \end{eqnarray*}y por lo tanto los puntos $D$, $E$, $F$ e $I$ están sobre una circunferencia $\mathsf{C}_{1}$.
Del mismo modo puede mostrarse que
\begin{eqnarray} \angle DEF + \angle FGD = 180^{\circ} \label{cic1} \end{eqnarray}y que
\begin{eqnarray} \angle DEH + \angle HID = 180^{\circ}. \label{cic2} \end{eqnarray}De (\ref{cic1}) se sigue que los puntos $D$, $E$, $F$ y $G$ están sobre una circunferencia $\mathsf{C}_{2}$ y de (\ref{cic2}) se sigue que los puntos $D$, $E$, $H$ y $I$ están sobre una circunferencia $\mathsf{C}_{3}$. Como $\mathsf{C}_{1} \cap \mathsf{C}_{2}\supseteq \{D, E, F\}$ y $\mathsf{C}_{1} \cap \mathsf{C}_{3}\supseteq \{D, E, I\}$ entonces $\mathsf{C}_{2} =\mathsf{C}_{1} = \mathsf{C}_{3}$. De todo esto se desprende que los puntos $D, E, F, G, H$ e $I$ están todos sobre una misma circunferencia.
Procedemos a determinar ahora el centro $\mathbf{Z}$ de la circunferencia que pasa por esos seis puntos. Consideremos la mediatriz $\ell$ del lado $DE$ del trapecio $DEGH$. Puesto que $\mathbf{Z}$ equidista de $D$ y $E$ entonces $\mathbf{Z} \in \ell$. Además, al ser $ADE$ un triángulo isósceles entonces $A \in \ell$. Por otro lado, como $DEGH$ es un trapecio isósceles se cumple que $\ell$ es también mediatriz del lado $GH$ del trapecio. Sea $X$ el punto medio del lado $GH$. Como $\triangle AGH$ es isósceles entonces $\angle XAH = \angle XAG$ y, por consiguiente, el segmento $AX$ está contenido en la bisectriz de $\angle CAB$. De esto y lo argumentado previamente se obtiene que $\mathbf{Z}$ está en la bisectriz de $\angle CAB$. Análogamente se puede establecer que $\mathbf{Z}$ pertenece también a las bisectrices de $\angle ABC$ y $\angle BCA$. Dado que tres rectas distintas tienen a lo más un punto en común, concluimos que el centro de la circunferencia que pasa por $D, E, F, G, H$ e $I$ es exactamente el incentro de $\triangle ABC$.
Expresaremos finalmente el radio $R$ de la circunferencia de los seis puntos (asociada a $\triangle ABC$) en función del inradio y el semiperímetro de $\triangle ABC.$ Para ello, nos auxiliaremos de la figura siguiente:
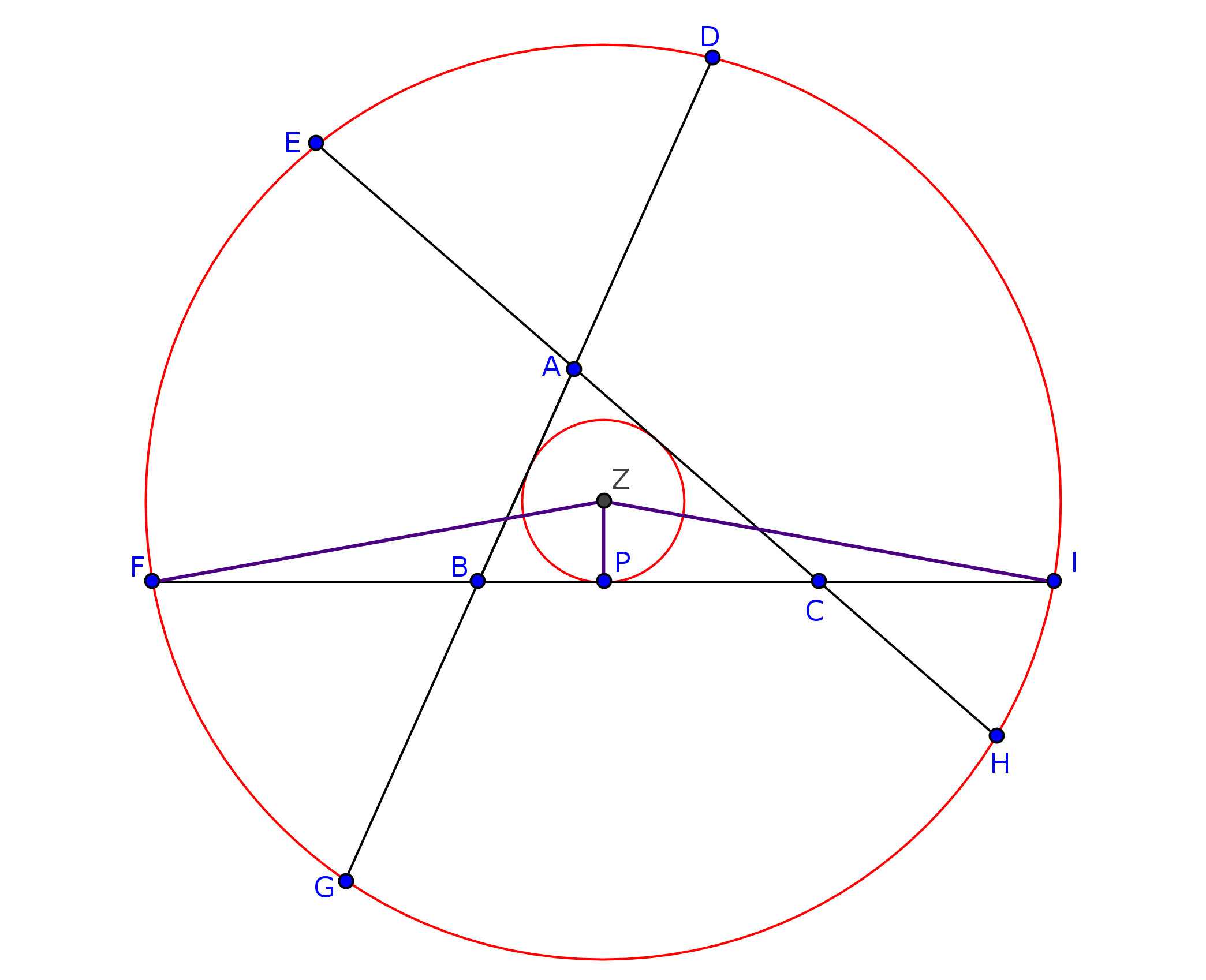
Supongamos que $\overline{AB}=c, \overline{BC}=a$ y $\overline{CA}=b$ y que el inradio del triángulo $ABC$ es $r$. Si $P$ es el pie de la perpendicular al lado $BC$ por $\mathbf{Z}$ entonces $\overline{\mathbf{Z}P}=r$. Además, como $F$ e $I$ están sobre la circunferencia de los seis puntos entonces $\overline{\mathbf{Z}F}=\overline{\mathbf{Z}I}$. De esta manera $\triangle P\mathbf{Z}F \cong \triangle P\mathbf{Z}I$ y en consecuencia
\begin{eqnarray*} \overline{FP} = \frac{\overline{FI}}{2} = \frac{\overline{FB}+\overline{BC}+\overline{CI}}{2} = \frac{b+a+c}{2}. \end{eqnarray*}Luego, si hacemos $s:= \frac{a+b+c}{2}$ y aplicamos el teorema de Pitágoras en $\triangle P\mathbf{Z}F$, llegamos a que
\begin{eqnarray} R^{2} = r^{2} + s^{2}. \label{inra-1} \end{eqnarray}De la igualdad anterior se tiene que $R$ se puede expresar sólo en términos de los lados de $\triangle ABC$. En efecto, es bien sabido que si $\Delta$ es el área de $\triangle ABC$ entonces
\begin{eqnarray}\Delta = sr \label{inra-2} \end{eqnarray}donde, al igual que antes, $s$ y $r$ denotan al semiperímetro e inradio del $\triangle ABC$ respectivamente. Por otra parte, la conocida fórmula de Herón dice que
\begin{eqnarray} \Delta =\sqrt{s(s-a)(s-b)(s-c)}. \label{inra-3} \end{eqnarray}De (\ref{inra-1}), (\ref{inra-2}) y (\ref{inra-3}) se colige que
\begin{eqnarray*} R = \sqrt{\frac{a^{2}b+a^{2}c+ab^{2}+cb^{2}+ac^{2}+bc^{2}+abc}{a+b+c}.} \end{eqnarray*}▢
En el thread de El irracional asociado a este problema, Malors Emilio Espinosa Lara estableció la conciclicidad de los puntos $D$, $E$, $F$, $G$, $H$ e $I$ de una manera distinta. Cabe mencionar que a la circunferencia que pasa por los extremos de las seis prolongaciones consideradas se le conoce como la circunferencia de Conway del triángulo $ABC$ (por ejemplo, ver [3D. Grinberg y E. W. Weisstein, Conway Circle. En internet: http://mathworld.wolfram.com/ConwayCircle.html ] o [6Tanya Khovanova, Conway's circle. En internet: http://blog.tanyakhovanova.com/2010/06/conways-circle/]; nótese, no obstante, que la fórmula que aparece en [3D. Grinberg y E. W. Weisstein, Conway Circle. En internet: http://mathworld.wolfram.com/ConwayCircle.html ] para el radio de la circunferencia de Conway de un triángulo en función de las longitudes de sus lados es errónea). En [6Tanya Khovanova, Conway's circle. En internet: http://blog.tanyakhovanova.com/2010/06/conways-circle/] puede encontrarse incluso la siguiente fotografía, en la cual el Prof. J. H. Conway aparece de espaldas luciendo una playera con un estampado alusivo a este teorema suyo:
© Tanya Khovanova
Por último, vale la pena añadir que cuando en octubre de 2013 le escribimos al Prof. Francisco Javier García Capitán para saber si él tenía más datos sobre el origen de este problema, su respuesta fue que no había escuchado de este interesante resultado previamente pero que, en cambio, vislumbraba una manera de generalizarlo. La generalización que obtuvo dio lugar al artículo [2F. J. García Capitán, A Generalization of the Conway Circle. Forum. Geom. 13, 2013, pp. 191-195 (ISSN 1534-1178). ], el cual fue publicado ese mismo año en la revista Forum Geometricorum.
Este problema también fue parte de los selectivos que se aplicaron en la Facultad de Ciencias de la UNAM para elegir al equipo que participaría en la XXII International Mathematics Competition. A la fecha no se han recibido soluciones en El irracional, pero les recordamos que los threads de todos los problemas siguen abiertos en espera de sus comentarios y soluciones. Presentamos a continuación una manera de abordarlo:
Supongamos que $A'B'C'D'$ es un cuadrado de lado $s$ y definamos $K'$, $L'$ análogamente a como se definen $K$ y $L$. Entonces $A'C'=s\sqrt 2$, $K'L'=s$, $A'L'=K'C'=s \cdot \frac{\sqrt{2}+1}{2}$ y $A'K'=L'C'=s\cdot \frac{\sqrt{2}-1}{2}$. Entonces,
\[ \frac{A'L'\cdot K'C'}{A'K'\cdot L'C'}=\frac{(\sqrt{2}+1)^2}{(\sqrt{2}-1)^2}=(\sqrt{2}+1)^4=17+12\sqrt{2}. \]Consideremos ahora un trapecio isósceles arbitrario $ABCD$ con incírculo $\omega$ y con $AB || CD$. Como no hay tres de $A$, $B$, $C$ y $D$ que sean colineales, entonces existe una transformación proyectiva $\tau$ que lleva $ABCD$ en un paralelogramo $A'B'C'D'$. Este mapa lleva $\omega$ a una cónica $\omega'$ tangente a los cuatro lados de $A'B'C'D'$. Sea $P=BC\cap AD$, y sea $\ell$ la recta por $P$ paralela a la recta $AB$. Entonces $\tau$ lleva $\ell$ a la recta al infinito. Como $\omega$ no intersecta a $\ell$, entonces $\omega'$ es una elipse. De este modo, componiendo $\tau$ con una transformación afín podemos suponer que $\omega'$ es un círculo.
Sean $W$, $X$, $Y$ y $Z$ los puntos de tangencia de $\omega$ con los lados $AB$, $BC$, $CD$ y $DA$ respectivamente y $W'$, $X'$, $Y'$, $Z'$ sus imágenes bajo $\tau$. Por simetría, la recta $WY$ pasa por la intersección de las rectas $BC$ y $AD$, y la recta $XZ$ es paralela a las rectas $AB$ y $CD$. De este modo, $W'Y'||B'C'||A'D'$ y $X'Z'||A'B'||C'D'$. Pero $\omega'$ es tangente a las rectas paralelas $A'B'$ y $C'D'$ en $W'$ y $Y'$, de modo que $W'Y'$ es un diámetro de $\omega'$ y $W'Y'\perp A'B'$, entonces $B'C'\perp A'B'$ y así $A'B'C'D'$ es un rectángulo. Por hipótesis, este rectángulo tiene una circunferencia inscrita, y es un hecho conocido que los cuadriláteros con circunferencia inscrita cumplen que $A'B'+C'D'=B'C'+D'A'$. Esto prueba que $A'B'C'D'$ es un cuadrado y así, estamos en el caso considerado al inicio del problema; si $K'$ y $L'$ son las intersecciones de $A'C'$ con $\omega'$ (con $K'$ entre $A'$ y $L'$), entonces $\frac{A'L'\cdot K'C'}{A'K'\cdot L'C'}=17+12\sqrt{2}$.
Ahora, $\tau$ lleva $\{K,L\}=AC\cap \omega$ a $\{K',L'\}=A'C'\cap \omega'$ (pero tal vez no en ese orden). Si $\tau(K)=K'$ y $\tau(L)=L'$ entonces, como las transformaciones proyectivas preservan razones cruzadas, tendríamos que
\[ \frac{AL\cdot KC}{AK\cdot LC}=\frac{A'L'\cdot K'C'}{A'K'\cdot L'C'}=17+12\sqrt{2}. \]Analicemos ahora el otro caso. Si $\tau(K)=L'$ y $\tau(L)=K'$, entonces obtendríamos que $\frac{AL\cdot KC}{AK\cdot LC}=\frac{1}{17+12\sqrt{2}} \lt 1$, lo cual es imposible pues $AL \gt AK$ y $KC \gt LC$. De esta forma, se sigue que $\frac{AL\cdot KC}{AK\cdot LC}=17+12\sqrt{2}$, como se quería mostrar.
▢
Hay otra forma de resolver el problema expresando las longitudes de los segmentos involucrados usando trigonometría. Dejamos este comentario como una sugerencia para que los lectores interesados den con una solución siguiendo ese enfoque.
La respuesta a ambas preguntas es no; así, basta dar un contraejemplo para el inciso b). Presentaremos la construcción propuesta por Omar Antolín Camarena en El irracional, que es la misma que teníamos en mente.
Tomemos los cuatro puntos $(0,0,0)$, $(1,1,0)$, $(1,0,1)$ y $(0,1,1)$. Notemos que la distancia entre cualesquiera dos de ellos es $\sqrt{2}$, por lo que son los vértices de un tetraedro regular. Consideremos a $F$ como el tetraedro (lleno) que tiene a estos puntos como vértices.
Primero mostraremos que la proyección en cada plano canónico es un cuadrado de lado $1$. En el plano $xy$ consideremos el cuadrado $C$ con vértices $(0,0)$, $(1,1)$, $(1,0)$ y $(0,1)$. Notemos que $F$ está contenido en $C\times \mathbb{R}$. Entonces la proyección de $F$ al plano $xy$ se queda contenida en $C$. Además, los vértices del tetraedro se proyectan a los vértices de $C$. Como $F$ es convexo, su proyección también. Esto muestra que la proyección es precisamente $C$. Por simetría, sucede lo análogo al proyectar en los planos $yz$ y $zx$.
Como $F$ es un tetraedro, entonces no es un cubo y se responde la pregunta a) negativamente. Falta mostrar que no contiene a ningún cuadrado de lado $1$. Notemos que un cuadrado de lado $1$ tiene diagonal $\sqrt{2}$. En $F$ los puntos más alejados son los vértices y justo están a distancia $\sqrt{2}$. Así que si $F$ contiene un cuadrado $ABCD$, la diagonal (digamos $AC$) debe estar sobre una arista de $F$. Como $BD$ cruza $AC$, a lo más uno de los puntos $B$ y $D$ está dentro de $F$. Esto da una contradicción, lo cual termina el problema.
▢
El inciso a) se puede responder de otras maneras; por ejemplo tomando el cubo $C$ cuyos vértices tienen entradas $0$ o $1$ y luego descartando un subconjunto $S\subseteq C$ bien elegido de modo que las proyecciones de $C\setminus S$ sigan siendo las mismas, pero la figura $C\setminus S$ no sea un cubo. Las soluciones aportadas por Yarza y David Cardona en El irracional a este inciso se basan en esta idea.A continuación, enunciamos los problemas 12, 13 y 14 de “El Baúl de Problemas”. Además de estos problemas, proponemos dos más. Estos cinco problemas se pueden encontrar en el foro El irracional
En la siguiente entrega platicaremos de los avances que tenemos en estos problemas y de las soluciones y comentarios que recibamos.
¡Hasta el próximo número!
[1] J. Hernández, Más sobre Erdös. En internet: http://elr3to.blogspot.mx/2011/08/mas-sobre-erdos.html
[2] F. J. García Capitán, A Generalization of the Conway Circle. Forum. Geom. 13, 2013, pp. 191-195 (ISSN 1534-1178).
[3] D. Grinberg y E. W. Weisstein, Conway Circle. En internet: http://mathworld.wolfram.com/ConwayCircle.html
[4] N. Hegyvári, On some irrational decimal fractions. Amer. Math. Monthly Vol. 100, 8, Oct. 1993, pp. 779-780.
[5] D. J. Newman, R. Breusch y F. Herzog, Solution to problem 4494. Amer. Math. Monthly Vol. 60, 9, Nov. 1953, pp. 632-633.
[6] Tanya Khovanova, Conway's circle. En internet: http://blog.tanyakhovanova.com/2010/06/conways-circle/
[7] Miscelánea Matemática, 20.
[8] Miscelánea Matemática, 21.
[9] E. M. Stein y R. Shakarchi, Real Analysis (Measure Theory, Integration, & Hilbert Spaces). Princeton University Press, Princeton NJ, USA, 2005, p. 235.


