

Ésta es la segunda parte del artículo sobre “El Baúl de Problemas” de la Miscelánea Matemática (una de las principales publicaciones periódicas de la Sociedad Matemática Mexicana). En la primera entrega del artículo presentamos nuestras soluciones a los primeros cinco de los diecinueve problemas que en su momento fueron propuestos en “El Baúl de Problemas”. Además, en la última sección del trabajo se listaron cinco problemas adicionales para que los entusiastas lectores de universo.math los abordaran y, en caso de resolverlos, compartieran sus soluciones en el foro El irracional.
En esta nueva entrega del artículo se presentarán las soluciones (y/u observaciones) que tenemos para los problemas 6, 7, 8 de “El Baúl de Problemas”. También comentaremos las soluciones que se recibieron en El irracional para estos problemas y para los problemas adicionales propuestos en la primera parte de este artículo. Al final de la nota, se plantearán más problemas de “El Baúl de Problemas” y dos problemas adicionales para que el lector intente resolverlos antes del próximo número de universo.math.
En este apartado se presentan las soluciones y observaciones que tenemos para los problemas 6, 7, 8 de “El Baúl de Problemas”. Los problemas cuyos enunciados están precedidos por un * son problemas cuya solución está acompañada de algunos comentarios adicionales que podrían resultar interesantes a los lectores.
Este problema es una de las múltiples variantes de uno clásico conocido como problema de Langley o problema de los ángulos adventicios (ver [3D. Gale, Tracking the automatic and (and other mathematical explorations), Springer-Verlag, New York, 1998., pp. 125-126] o [8C. Tripp, Adventitious angles, Math. Gaz. 59, núm, 408, 1998, pp. 98-106., pp. 98-106]). Es posible abordar este problema mediante trigonometría (tal como lo mostró Omar Antolín Camarena en El irracional), pero hemos optado por presentar en primer lugar una solución geométrica simple que depende solamente de un par de trazos auxiliares. Recuérdese que el objetivo que se persigue al realizar trazos auxiliares en el diagrama asociado con un problema geométrico es obtener información que no es tan inmediata de las hipótesis del problema y que pudiere incidir en la resolución del mismo.
En el problema que nos ocupa realizaremos dos trazos auxiliares: primero, la paralela por $D$ al lado $BC$ de $\triangle ABC$ y después, el segmento de recta que une al vértice $C$ de $\triangle ABC$ con la intersección de $AB$ y la paralela previamente construida. Llamemos $F$ al punto de intersección de la paralela a $BC$ por $D$ con el lado $AB$ de $\triangle ABC$ y $G$ a la intersección de $CF$ con $BD$. La situación al momento es la que se indica en la siguiente figura:
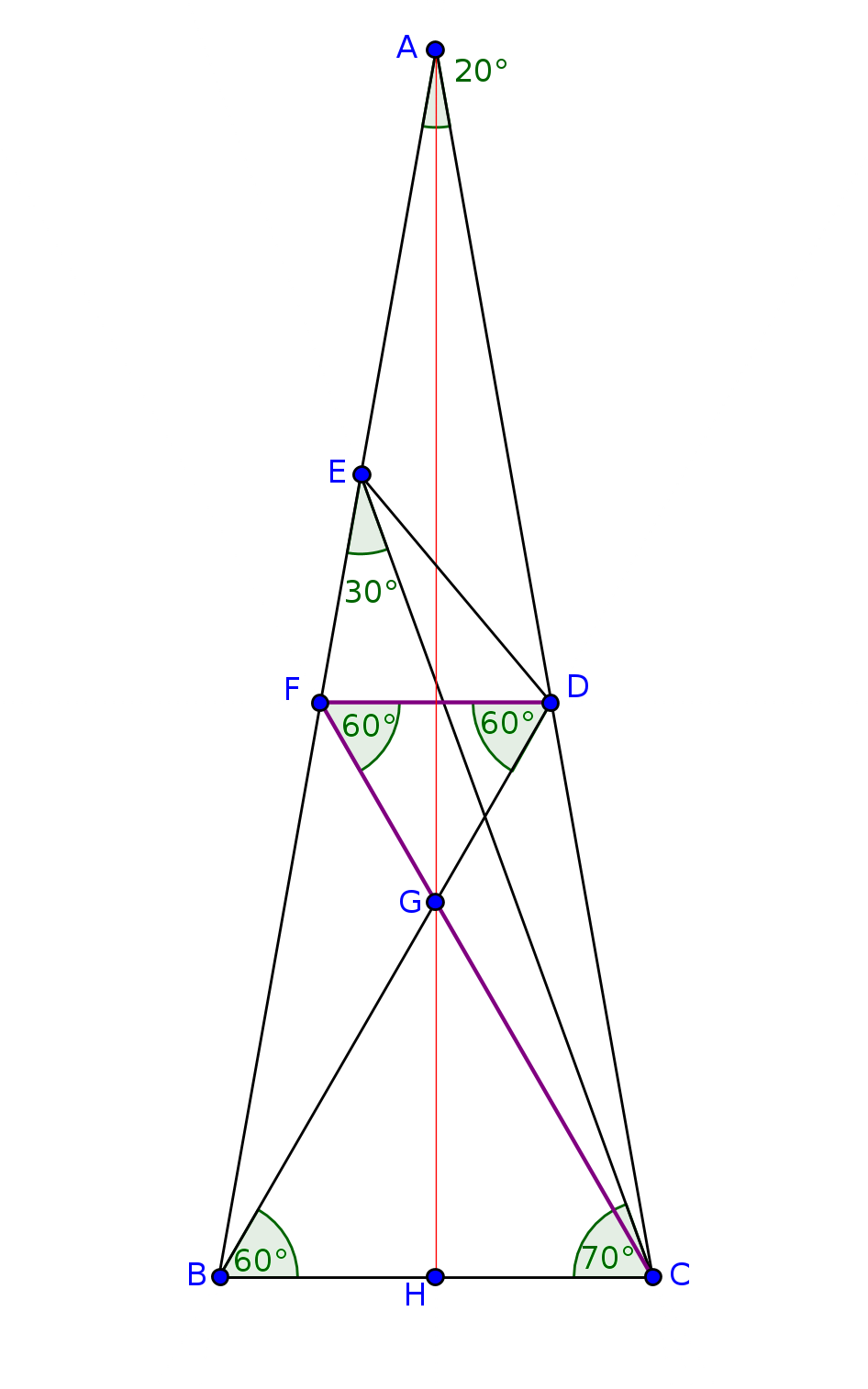
Como $\triangle DFG$ tiene todos sus ángulos de $60^\circ$, entonces es un triángulo equilátero. Tenemos también que $\triangle AFC$ es isósceles pues tiene dos ángulos de $20^\circ$.
Notemos que, por simetría en $\triangle ABC$, se sigue que $G$ está en la altura por $A$. En consecuencia, $\angle ACE=10^\circ=\angle GAC$ y, por lo tanto, $G$ y $E$ son puntos simétricos en $\triangle FAC$. De esta manera, $\overline{FE}=\overline{FG}=\overline{FD}$ y el triángulo $FED$ es isósceles.
Como sabemos que $\angle EFD = \angle ABC = 80^\circ$, entonces, \begin{eqnarray*}\angle FED = \frac{180^\circ-80^\circ}{2}=50^\circ\end{eqnarray*} y, por consiguiente: \[\angle{CED}=\angle FED-\angle FEC=50^\circ-30^\circ=20^\circ.\]
Comentaremos ahora la solución trigonométrica que Omar Antolín Camarena publicó recientemente en El irracional. En esta solución se prueba que los triángulos $CED$ y $CAE$ son semejantes. Puesto que esos triángulos tienen en común el ángulo $C$, para establecer su semejanza, lo único que se tiene que mostrar es que \begin{eqnarray} \frac{\overline{CE}}{\overline{CA}} = \frac{\overline{CD}}{\overline{CE}}. \label{senos0} \end{eqnarray}
Las razones que aparecen en la igualdad anterior se pueden reescribir de la siguiente manera: aplicando la ley de los senos en $\triangle CEA$ se obtiene que \begin{eqnarray} \frac{\overline{CE}}{\overline{CA}} = \frac{\mathrm{sen} \angle EAC}{\mathrm{sen} \angle CEA} = \frac{\mathrm{sen} 20^\circ}{\mathrm{sen} 150^\circ}. \label{senos1} \end{eqnarray}
Por otra parte, al aplicar la ley de los senos en los triángulos $BEC$ y $BCD$ llegamos a que \begin{eqnarray} \frac{\overline{CD}}{\overline{CE}} = \frac{\overline{CD}}{\overline{BC}} \cdot \frac{\overline{BC}}{\overline{CE}} = \frac{\mathrm{sen} \angle CBD}{\mathrm{sen} \angle BDC} \cdot \frac{\mathrm{sen} \angle BEC}{\mathrm{sen} \angle EBC} = \frac{\mathrm{sen} 60^\circ}{\mathrm{sen} 40^\circ} \cdot \frac{\mathrm{sen} 30^\circ}{\mathrm{sen} 80^\circ}. \label{senos2} \end{eqnarray}
Así, todo se ha reducido a demostrar que \begin{eqnarray*} \frac{\mathrm{sen} 20^\circ}{\mathrm{sen} 150^\circ} = \frac{\mathrm{sen} 60^\circ}{\mathrm{sen} 40^\circ} \cdot \frac{\mathrm{sen} 30^\circ}{\mathrm{sen} 80^\circ}. \end{eqnarray*} Esta igualdad es equivalente a \begin{eqnarray*} 4 \mathrm{sen} 20^\circ \mathrm{sen} 40^\circ \mathrm{sen} 80^\circ = \mathrm{sen} 60^\circ, \end{eqnarray*} la cual es, a su vez, un caso particular de la identidad \begin{eqnarray*} 4\mathrm{sen} x\, \mathrm{sen}(60^\circ - x)\, \mathrm{sen}(60^\circ+x) = \mathrm{sen}(3x). \end{eqnarray*}
Esta identidad trigonométrica puede ser deducida utilizando las fórmulas de producto a suma. Específicamente, las identidades que nos interesan son: \begin{eqnarray*} 2 \mathrm{sen} a\, \mathrm{sen} b = \cos(a-b)-\cos(a+b) \quad \text{ y } 2\mathrm{sen} a \cos b = \mathrm{sen}(a+b)+\mathrm{sen}(a-b) \end{eqnarray*} Comenzamos usando la primera identidad para $a=60^\circ - x$ y $b=60^\circ + x$: \begin{eqnarray*} 2 \mathrm{sen}(60^\circ - x)\, \mathrm{sen}(60^\circ + x) = \cos(-2x)-\cos(120^\circ) = \cos{2x}+\frac{1}{2}. \end{eqnarray*} Para terminar, usamos ahora la segunda identidad tomando $a=x$ y $b=2x$: \begin{multline*} 4 \mathrm{sen} x\, \mathrm{sen}(60^\circ - x) \mathrm{sen}(60^\circ + x) = \mathrm{sen} x\cos(2x)+\mathrm{sen} x \\ = \left(\mathrm{sen}(3x)+\mathrm{sen}(-x)\right)+\mathrm{sen} x = \mathrm{sen}(3x). \end{multline*}
▢
Definamos la siguiente función: \begin{eqnarray*} f(n,k) := \frac{1}{ 2\pi} \int_{-\pi}^{\pi}\left(2\cos\left(\frac{x}{2}\right)\right)^{n}\cos \left(\frac{n}{2}-k \right)x\,dx \end{eqnarray*} Fácilmente se puede mostrar que $f(0,0)=1$ y $f(1,0)=f(1,1)=1.$ Demostraremos a continuación que, para cada $n\geq 2$, se cumple que \begin{eqnarray}f(n,0)=1=f(n,n). \label{aserto2}\end{eqnarray} La demostración dependerá de las siguientes fórmulas de reducción, las cuales son una consecuencia directa de la fórmula de Euler (para $\theta \in \mathbb{R}$, $e^{i\theta} =\cos \theta + i\, \mathrm{sen} \theta$) y del teorema del binomio.
Para $n \in \mathbb{N}$ impar \begin{eqnarray} \cos^n \theta &=& \frac{2}{2^n} \sum_{k=0}^{\frac{n-1}{2}} \binom{n}{k} \cos{((n-2k)\theta)} \label{reduc1} \end{eqnarray} y para $n \in \mathbb{N}$ par \begin{eqnarray} \cos^n \theta &=& \frac{1}{2^n} \binom{n}{\frac{n}{2}} + \frac{2}{2^n} \sum_{k=0}^{\frac{n}{2}-1} \binom{n}{k} \cos{((n-2k)\theta)}. \label{reduc2} \end{eqnarray}
Bajo la luz de (\ref{reduc1}) se sigue que, si $n\geq 2$ es un número natural impar, entonces: \begin{eqnarray} f(n,0) &=& \frac{1}{2\pi} \int_{-\pi}^{\pi}\left(2\cos\left(\frac{x}{2}\right)\right)^{n}\cos \left(\frac{n}{2} \right)x\,dx \nonumber\\ &=& \frac{2^{n}}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} (\cos^{n} \theta) \cos n\theta\, d\theta \nonumber\\ &=& \frac{2}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \sum_{k=0}^{\frac{n-1}{2}} \binom{n}{k} \cos{((n-2k)\theta)} \cos n\theta\, d\theta \nonumber\\ &=& \frac{2}{\pi} \sum_{k=0}^{\frac{n-1}{2}} \binom{n}{k} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos{((n-2k)\theta)} \cos n\theta\, d\theta \label{paso}\\ &=& \frac{2}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos^{2} n\theta\, d\theta \label{paso2}\\ &=& \frac{2}{\pi} \cdot \frac{1+\cos 2n\theta}{2} \bigg|_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \nonumber\\ &=&1 \nonumber. \end{eqnarray}
Por otro lado, si $n\geq 2$ es un número natural par, al aplicar la fórmula en (\ref{reduc2}) y proceder como en el caso previo, se obtiene que: \begin{eqnarray*} f(n,0) &=& \frac{2^{n}}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} (\cos^{n} \theta) \cos n\theta\, d\theta\\ &=& \frac{1}{\pi} \binom{n}{\frac{n}{2}}\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos n\theta\, d\theta + \frac{2}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos^{2} n\theta\, d\theta\\ &=& \frac{2}{\pi} \int_{\frac{-\pi}{2}}^{\frac{\pi}{2}} \cos^{2} n\theta\, d\theta\\ &=& 1. \end{eqnarray*}
De los dos párrafos previos y la paridad de la función coseno se desprende la veracidad de lo enunciado en (\ref{aserto2}).
Supondremos ahora que la identidad en cuestión se cumple para $n-1$ y para cada $k \in \{1,2 \ldots, n-1\}$, esto es, que \begin{eqnarray*} \binom{n-1}{k} = f(n-1,k) \end{eqnarray*} para cada $k \in \{1,2,\ldots, n-1\}$. De este supuesto y de la conocida identidad de Pascal para los coeficientes binomiales se sigue que si $j \in \{1,\ldots, n-1\}$, entonces, \begin{eqnarray*} \binom{n}{j} &=& \binom{n-1}{j-1} + \binom{n-1}{j}\\&=& \frac{1}{2\pi}\int_{-\pi}^{\pi} \left(2\cos\left(\frac{x}{2}\right)\right)^{n-1}\cos \left(\frac{n-1}{2}-(j-1)\right)x\,dx\\ &+& \frac{1}{2\pi}\int_{-\pi}^{\pi} \left(2\cos\left(\frac{x}{2}\right)\right)^{n-1}\cos \left(\frac{n-1}{2}-j\right)x\,dx\\ &=& \frac{1}{2\pi}\int_{-\pi}^{\pi} \left(2\cos\left(\frac{x}{2}\right)\right)^{n-1} \left\{\cos\left(\frac{n-1}{2}-(j-1)\right)x + \cos\left(\frac{n-1}{2}-j\right)x\right\}\, dx. \end{eqnarray*}
La suma que aparece en llaves se puede expresar como un producto a través de la conocida identidad de prostaféresis: \begin{eqnarray*} \cos \alpha \cos \beta = \frac{\cos(\alpha-\beta)+\cos(\alpha+\beta)}{2}. \end{eqnarray*} En efecto, si hacemos $\alpha = \frac{n-2j}{2}x$ y $\beta = -\frac{x}{2}$, entonces: \begin{eqnarray*} \alpha-\beta = \frac{n-2j+1}{2}x = \left(\frac{n-1}{2}-(j-1)\right)x, \end{eqnarray*} \begin{eqnarray*} \alpha+\beta = \frac{n-2j-1}{2}x = \left(\frac{n-1}{2}-j\right)x \end{eqnarray*} y, por consiguiente: \begin{eqnarray*} \binom{n}{j} &=& \frac{1}{\pi} \int_{-\pi}^{\pi} \left(2\cos\left(\frac{x}{2}\right)\right)^{n-1}\left(\cos\left(\frac{n-2j}{2}\right)x\right) \cos\left(-\frac{x}{2}\right) \, dx\\ &=& \frac{1}{2\pi} \int_{-\pi}^{\pi} \left(2\cos\left(\frac{x}{2}\right)\right)^{n} \cos\left(\frac{n}{2}-j\right)x\, dx\\ &=& f(n,j). \end{eqnarray*}
Puesto que ya se tenía que $f(n,0)=f(n,n)= 1= \binom{n}{n} = \binom{n}{0}$, la prueba termina.
▢
A continuación presentamos una solución para el inciso a) que es una ligera modificación de la solución presentada por Israel Jalpa Rico en El irracional.
Denotemos como $h$ a la altura perpendicular al lado de longitud $f_n$. Luego, tenemos que: $$f_{n-1}^2=\left(\frac{f_n}{2}\right)^2+h^2$$ Además, si $A$ es el área del triángulo, entonces: $$2A=f_n\sqrt{f_{n-1}^2-\left(\frac{f_n}{2}\right)^2},$$ de donde: \begin{eqnarray} 16A^2=f_n^2\left(4f_{n-1}^2-f_n^2\right) \label{feven}. \end{eqnarray}
$(\leftarrow)$ Si $n=6$, entonces $f_5=5$ y $f_6=8$, por lo que $A=12$ y, entonces, el triángulo es de Herón.
$(\rightarrow)$ Ahora, si el triángulo es de Herón, entonces $A\in\Bbb Z$. Si $f_n$ fuera impar, entonces, el lado derecho de (\ref{feven}) también lo sería, lo cual es una contradicción pues es el entero par $16 A^2$. De esta forma, $f_n=2\ell$. Substituyendo en (\ref{feven}) y, simplificando, tenemos $$A^2=f_n^2(f_{n-1}^2-\ell^2).$$ Como el lado izquierdo es un cuadrado y $f_{n-1}^2$ también, entonces $f_{n-1}^2-\ell^2$ también lo es; de esta forma, existe un entero $r$ tal que \begin{eqnarray} r^2+\ell^2=f_{n-1}^2 \label{pita}. \end{eqnarray}
Ahora se demostrarán los siguientes dos lemas:
Demostración. Tenemos que $\gcd(a,a+b)\mid a, a+b$ por lo que $\gcd(a,a+b)\mid -a+(a+b)=b$ y luego $$\gcd(a,a+b)\leq\gcd(a,b).$$ Además, como $\gcd(a,b)\mid a, b$, entonces $\gcd(a,b)\mid a+b$ y luego se sigue que $$\gcd(a,b)\leq\gcd(a,a+b).$$ Por lo tanto, $\gcd(a,a+b)=\gcd(a,b)$.
▢
Demostración. Se procede por inducción sobre $n$. Si $n=0$ entonces $f_0=0$ y $f_1=1$ por lo que la proposición es verdadera en este caso. Ahora supongamos que para cada $n\geq 1$ se tiene que $\gcd(f_n,f_{n+1})=1$. Luego, $\gcd(f_{n+1},f_{n+2})=\gcd(f_{n+1},f_{n+1}+f_n)$ y, por el Lema 1, $\gcd(f_{n+1},f_{n+2})=\gcd(f_{n+1},f_n)$, que por hipótesis inductiva es $1$. Con esto queda verificado el paso inductivo.
▢
Como $\gcd(f_{n-1},f_n)=1$ por el Lema 2, entonces es fácil ver que $$\gcd\left(f_{n-1},\frac{f_n}{2},h\right)=1,$$ de modo que tenemos una terna pitagórica primitiva en (\ref{pita}). Un resultado conocido [4I. Niven, H. S. Zuckerman, H. L. Montgomery, An introduction to the theory of numbers, quinta edición, Wiley, 1991.] afirma que existen $k,m\in\Bbb Z$ con $k\geq m$ tales que, o bien, $$f_{n-1}=k^2+m^2, \quad \frac{f_n}{2}=\ell=2km,\quad r=k^2-m^2,$$ o bien, $$f_{n-1}=k^2+m^2, \quad \frac{f_n}{2}=\ell=k^2-m^2,\quad r=2km.$$
En el primer caso, se sigue trabajando con la recursión de Fibonacci hacia atrás que $f_{n-3}=2(k-m)^2$. De manera similar, en el segundo caso se sigue que $f_{n-3}=(2m)^2$. Ahora citamos el siguiente resultado de John Cohn [2J.H.E. Cohn, On square Fibonacci nubmers, J. London Math. Soc., 39, 1964, pp. 537-541., pp. 537-541]
En cualquiera de los casos esto reduce el problema a verificar manualmente los valores $n=3,4,5,6,9,15$. La única posibilidad es $n=6$.
▢
Todavía no tenemos una solución para el inciso b) de este problema. En la solución del inciso a) se cita el resultado de Cohn acerca de cuáles números de Fibonacci son cuadrados perfectos. Notemos que $8$ es un cubo perfecto y un número de Fibonacci. En 2006, Bugeaud, Mignotte y Siksek probaron que $0$, $1$, $8$ y $144$ son los únicos números de Fibonacci que, a la vez, son potencias perfectas [1Y. Bugeaud, M. Mignotte, S. Siksek, Classical and modular approaches to exponential Diophantine equations I. Fibonacci and Lucas perfect powers, Annals of Mathematics 163, 2006, pp. 969-1018., pp. 969-1018].
(Solución por Raúl Astudillo) Escribamos el polinomio como $f(x)=ax^2+bx+c$, donde $a>0$. Notamos que: \[ \frac{\frac{1}{n^2}}{\frac{1}{f(n)}} = a + \frac{b}{n}+\frac{c}{n^2}. \]
De esto se ve que $\lim_{n\to \infty} \frac{\frac{1}{n^2}}{\frac{1}{f(n)}}$ existe y es igual a $a$. Ya que la serie $\sum_{n=1}^\infty \frac{1}{n^2}$ es convergente, lo anterior implica que $\sum_{n=1}^\infty \frac{1}{f(n)}$ también lo es.
Supongamos ahora que ${\bf P}\subseteq f(\mathbb{N})$. Entonces \[ \sum_{p\in {\bf P}} \frac{1}{p}\leq \sum_{n=1}^\infty \frac{1}{f(n)}. \]
Sin embargo, es bien conocido que $\sum_{p\in {\bf P}} \frac{1}{p}=\infty$, así que la desigualdad anterior contradice que $\sum_{n=1}^\infty\frac{1}{f(n)}$ sea convergente. Concluimos que no existe tal polinomio que satisfaga lo querido.
▢
Recibimos también la siguiente solución. Utiliza el teorema de los números primos.
(Solución por Omar Antolín) Si $f$ es un polinomio (en una variable) de grado $k$, el número de valores que puede tomar entre $1$ y $N$ es $O(N^{1/k})$, que para $k>1$ es menos que la cantidad de primos que hay por el teorema de los números primos.
▢
Para los lectores interesados, la divergencia de la suma $\sum_{p\in {\bf P}} \frac{1}{p}$ se puede consultar en un libro de texto de teoría de números, por ejemplo en [4I. Niven, H. S. Zuckerman, H. L. Montgomery, An introduction to the theory of numbers, quinta edición, Wiley, 1991.]. Una prueba del teorema de los números primos apareció en la Miscelánea Matemática [7J. Ramos, El teorema de los números primos, Miscelánea Matemática 38, 2003, pp. 15-31., pp. 15-31].
Este fue un problema de la International Mathematics Competition. La siguiente solución, recibida en el foro El irracional, es muy similar a la solución oficial.
(Solución por Omar Antolín) Elevando la igualdad $\sum_{i=1}^n \lambda_i = \text{tr}(A)=\sum_{i=1}^n a_{ii}$ al cuadrado, vemos que la desigualdad pedida es equivalente a $\text{tr}(A^2)=\sum_{i=1} ^n \lambda_i^2 \geq \sum_{i=1}^n a_{ii}^2$. Esta desigualdad es clara pues, por la simetría de $A$, tenemos que: \[ \text{tr}(A^2)=\text{tr}(AA^{T})=\sum_{1\leq i,j,\neq n} a_{ij}^2\geq \sum_{i=1}^n a_{ii}^2. \]
La igualdad se da si y sólo si los otros términos de $\sum_{1\leq i,j,\neq n} a_{ij}^2$ son cero, si y sólo si $a_{ij}=0$ siempre que $i\neq j$, o sea, cuando $A$ es diagonal.
▢
A continuación, enunciamos los problemas 9, 10 y 11 de “El Baúl de Problemas”. Además de estos problemas, anexamos a la lista otros dos. Estos cinco problemas se pueden encontrar en el foro El irracional en donde es posible comentarlos y/o presentar una solución para ellos.
En la siguiente entrega del artículo presentaremos los avances que tenemos en estos problemas; asimismo, les platicaremos sobre las soluciones y comentarios que se recolecten en El irracional.
¡Hasta el próximo número!
[1] Y. Bugeaud, M. Mignotte, S. Siksek, Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers, Annals of Mathematics, 163, 2006, pp. 969-1018.
[2] J.H.E. Cohn, On square Fibonacci numbers, J. London Math. Soc. 39, 1964, pp. 537-541.
[3] D. Gale, Tracking the automatic and (and other mathematical explorations), Springer-Verlag, New York, 1998.
[4] I. Niven, H. S. Zuckerman, H. L. Montgomery, An introduction to the theory of numbers, quinta edición, Wiley, 1991.
[5] Miscelánea Matemática, 19.
[6] Miscelánea Matemática, 20.
[7] J. Ramos, El teorema de los números primos, Miscelánea Matemática 38, 2003, pp. 15-31.
[8] C. Tripp, Adventitious angles, Math. Gaz. 59, núm. 408, 1998, pp. 98-106.


