Billares poligonales y curvas de Teichmüller II

Éste es el segundo y último de dos artículos donde explicamos la relación entre los billares poligonales y las curvas de Teichmüller. La primera parte apareció en el volumen anterior de esta revista [15]F. Valdez, Billares poligonales y curvas de Teichmüller, universo.math, 1 núm. 2 (2014) artículo 4..

En la primera parte de este texto vimos cómo a toda mesa de billar poligonal racional (recordemos que aquí racional quiere decir que todos los ángulos interiores de $P$ son múltiplos racionales de $\pi$) se le puede asociar una superficie plana $S_P$. De esta manera, convertíamos el estudio de la dinámica de una bola de billar en $P$ en el estudio del flujo geodésico en $S_P$. Posteriormente, vimos que la superficie $S_P$ puede entenderse como un objeto analítico. Esta interpretación nos permite situar a $S_P$ en el espacio móduli de todas las superficies planas compactas de género fijo $g$, que denotamos por $\Omega^*\mathcal{M}_g$.

En esta segunda parte, definiremos una acción geométrica del grupo $\rm SL(2,\mathbb{R})$ sobre $\Omega^*\mathcal{M}_g$ y veremos cómo este sistema dinámico está relacionado con la dinámica del billar a través de las curvas de Teichmüller.

Acción de $\rm SL(2,\mathbb{R}) $ sobre $\Omega^*\mathcal{M}_g$ y curvas de Teichmüller

Consideremos una superficie plana $S$ con su atlas $\mathcal{A}=\{(U,\varphi)\}$ y una matriz $A\in{\rm SL(2,\mathbb{R})}$. Al postcomponer cada una de las cartas de $\mathcal{A}$ con la función lineal que define $A$, obtenemos un nuevo atlas $A\cdot\mathcal{A}:=\{(U,A\cdot\varphi)\}$ para $S$. Es fácil verificar que este atlas define una nueva estructura de superficie plana sobre $S$. Denotamos a $S$ con esta nueva estructura como $A\cdot S$. y así tenemos una acción de $\rm SL(2,\mathbb{R})$ sobre $\Omega^*\mathcal{M}_g$, que ilustramos en la figura 1.

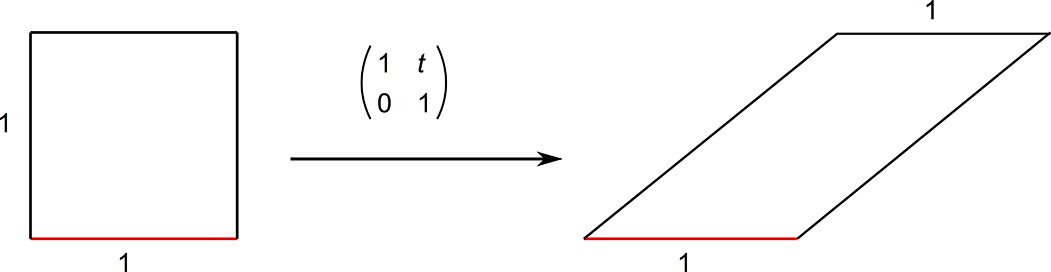
La acción que acabamos de definir también tiene un sabor analítico. Para esto recordemos que toda superficie plana se puede pensar como una pareja $(X,\omega)$ donde $X$ es superficie de Riemann y $\omega$ es una 1-forma holomorfa. Así, si $A= (\begin{smallmatrix} a & b\\ c & d \end{smallmatrix})$, la 1-forma: $$ \eta = \begin{pmatrix} 1 & i \end{pmatrix} \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} Re(\omega) \\ Im(\omega) \end{pmatrix} $$ es armónica (no necesariamente holomorfa) en $X$. Sin embargo, existe una única estructura de superficie de Riemann $Y$ para la superficie topológica subyacente a $X$ con respecto a la cual $\eta$ es holomorfa. Así, podemos definir: $$ A\cdot(X,\omega):=(Y,\eta) $$ Desde este punto de vista, es claro que la acción de ${\rm SL(2,\mathbb{R})}$ a priori no sólo cambia la estructura plana, sino también la estructura conforme subyacente. Decimos a priori porque el cambio de la estructura conforme no siempre se da; por ejemplo, si $A\in{\rm SO(2,\mathbb{R})}$, tenemos que $A\cdot (X,\omega)=(X,\eta)$ dado que las rotaciones son transformaciones holomorfas.

Para poder definir lo que es una curva de Teichmüller es necesario primero entender cómo las llamadas geodésicas complejas son generadas por las superficies planas.

Geodésicas complejas

Supongamos que existe una función holomorfa $$ \mathbb{H}^2\stackrel{f}{\longrightarrow}\mathcal{M}_g $$ entre el plano hiperbólico provisto de la métrica de curvatura -4 y el espacio de móduli $\mathcal{M}_g$ provisto de la métrica de Teichmüller. Un teorema de Royden nos dice que $f$ es, o bien una contracción o bien una isometría. En el segundo caso, se dice que $f$ parametriza una geodésica compleja. Como veremos en los siguientes párrafos, toda superficie plana $(X,\omega)$ da origen a una geodésica compleja.

Para cada $(X,\omega)$ consideremos la función $$ {\rm SL(2,\mathbb{R})}\stackrel{F}{\longrightarrow}\Omega^*\mathcal{M}_g$$ definida como $F(A):=A\cdot(X,\omega)$ y denotemos por $Proj_g(X,\omega)=X$ la proyección que olvida la 1-forma $\omega$. Así, la función $$ \rm SO(2,\mathbb{R})\backslash SL(2,\mathbb{R}) \stackrel{\tilde{f}}{\longrightarrow}\mathcal{M}_g $$ dada por $ \tilde{f}[A]=Proj_g(A\cdot(X,\omega))$ está bien definida y hace conmutar el diagrama.

El cociente $\rm SO(2,\mathbb{R})\backslash SL(2,\mathbb{R})$ se identifica con el plano hiperbólico $\mathbb{H}^{2}$. En efecto, la función $\rm SL(2,\mathbb{R})\stackrel{\rho}{\longrightarrow} \mathbb{H}^2$ definida como $$ \rho(A):=-\overline{A^{-1}}(i) $$ produce al pasar al cociente una biyección entre $\rm SO(2,\mathbb{R})\backslash SL(2,\mathbb{R}) $ y el plano hiperbólico $\mathbb{H}^2$. Esta biyección nos permite factorizar $\tilde{f}$ y obtener una geodésica compleja \begin{equation} \label{E:ComplexGeodesic} \mathbb{H}^2\stackrel{f}{\longrightarrow}\mathcal{M}_g. \end{equation} Llamamos a la función $f$ la geodésica compleja generada por la superficie plana $(X,\omega)$.

Definición 1.

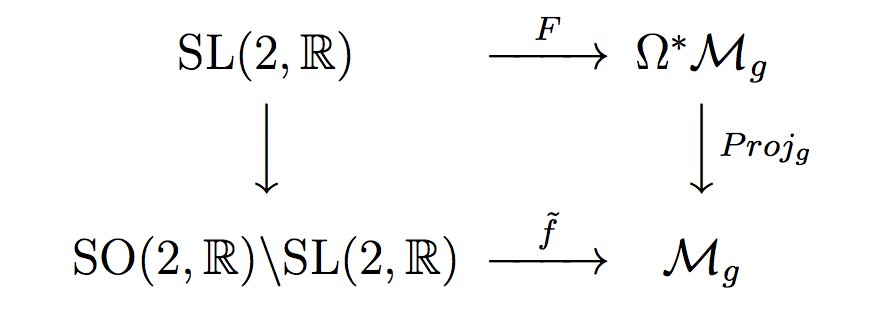
De la definición se deduce que todas las superficies planas en la $\rm SL(2,\mathbb{R})$-órbita de $(X,\omega)$ generan la misma geodésica compleja y, si es el caso, la misma curva de Teichmüller.

Para entender cuándo una superficie plana genera una curva de Teichmüller y la relación que tiene ésta con la dinámica del billar es necesario introducir el trabajo de W. Veech.

El grupo y la dicotomía de Veech

Dada una superficie plana $(X,\omega)$, llamamos homeomorfismo afín de $(X,\omega)$ a toda función invertible $f:X\to X$ que preserve la orientación, deje invariante el conjunto de ceros $Z(\omega)$ de la 1-forma y que, en coordenas locales del atlas de superficie plana de $X\setminus Z(\omega)$, se escriba de manera afín. Esto es, $f$ localmente tiene la forma \begin{equation} \label{E:HomeoAfin} \begin{pmatrix} x \\ y \end{pmatrix} \rightsquigarrow A \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} \lambda_1 \\ \lambda_2 \end{pmatrix} \end{equation} donde $A= (\begin{smallmatrix} a & b\\ c & d \end{smallmatrix})\in {\rm GL_+(2,\mathbb{R})}$ y $\lambda_{1},\lambda_{2}\in\mathbb{R}$. El conjunto de todos los homeomorfismos afines de $(X,\omega)$ forma un grupo que denotamos por $\rm Aff_{+}(X,\omega)$. Observemos que:

1. Dado que $X\setminus Z(\omega)$ tiene un atlas donde los cambios de coordenadas son translaciones, la matrix $A$ que aperece en (\ref{E:HomeoAfin}) no depende de las coordenas en las que estemos. Esto implica que la función \begin{equation} \label{E:GrupoVeech} \rm Aff_+(X,\omega)\stackrel{D}{\longrightarrow} GL_+(2,\mathbb{R}) \end{equation} que asigna a cada $f$ su parte diferencial $Df=A$ está bien definida y es un morfismo de grupos.
2. Dado que $X\setminus Z(\omega)$ tiene un atlas donde los cambios de coordenadas son translaciones podemos, vía pullback, jalar la forma de área del plano euclideano y obtener una forma de área sobre $X$. Así, el área de $X$ con respecto a dicha forma es un invariante bajo cualquier homeomorfismo afín y esto implica que, en realidad, $A$ en (\ref{E:HomeoAfin}) es un elemento de $\rm SL(2,\mathbb{R})$.

Definición 2.

Para superficies compactas, el grupo de Veech $\rm SL(X,\omega)$ es un subgrupo discreto de $\rm SL(2,\mathbb{R})$ que, además, nunca es cocompacto [6]P. Hubert, T. A. Schmidt, An introduction to Veech surfaces, Handbook of dynamical systems. Vol. 1B, Elsevier B. V., Amsterdam, 2006, 501—526.. Lo que es más, genéricamente $\rm SL(X,\omega)$ es o bien trivial o bien isomorfo a $\mathbb{Z}^{2}$. Sin embargo, en los casos especiales en los que el grupo de Veech es grande, el tamaño del mismo repercute en la dinámica del flujo geodésico.

Baby example: el toro

Usando el hecho de que el plano es el cubriente universal del toro no es difícil probar que el grupo de Veech $\mathbb{R}^2/\mathbb{Z}^2$ es ${\rm SL}(2,\mathbb{Z})$. Ahora bien, un resultado clásico debido a Weyl nos dice que, dada una dirección $\theta\in \mathbb{R}/2\pi\mathbb{Z}$, el flujo geodésico en el toro paralelo a dicha dirección es:

1. Periódico si y sólo si $\theta$ es un múltiplo racional de $\pi$.
2. Únicamente ergódico (con respecto a la medida de Lebesgue) en el resto de los casos

Esta dicotomía tiene consecuencias inmediatas para el billar en el cuadrado o en el triángulo equilátero: toda trayectoria que no termine en una buchaca es cerrada o se distribuye de manera uniforme en la mesa.

Por otro lado, $\rm SL(2,\mathbb{Z})$ actúa por transformaciones de Moebius sobre $\mathbb{H}^2$ y el cociente $\mathbb{H}^2/{\rm SL(2,\mathbb{Z})}$ tiene área hiperbólica finita (es justo la curva modular); es decir, $\rm SL(2,\mathbb{Z})$ es una retícula.

El siguiente resultado nos dice que esta coincidencia entre presentar una dicotomía en la dinámica del flujo geodésico y tener un grupo de Veech que sea una retícula no es, en realidad, pura coincidencia:

Teorema 1.

Dicho de otra manera, si el grupo de Veech es suficientemente grande (en sentido hiperbólico), entonces, la dinámica del flujo geodésico en la superficie plana correspondiente es tan simple como la dinámica del flujo geodésico en un toro.

Relación entre curvas de Teichmüller y grupos de Veech

Teorema 2.

La prueba de este teorema puede encontrarse en [11]C. T. McMullen, Billiards and Teichmüller curves on Hilbert modular surfaces, J. Amer. Math. Soc., 16 no. 4 (2003) 857—885. (o más detallada en [5]F. Herrlich, G. Schmithüsen, On the boundary of Teichmüller disks in Teichmüller and in Schottky space, Handbook of Teichmüller theory. Vol. I, IRMA Lect. Math. Theor. Phys. 11, Eur. Math. Soc., Zürich, 2007, 293—349. , § 2.3 y § 2.4). A grandes rasgos, si denotamos por $\rm Stab(X,\omega)$ al estabilizador de la superficie plana $(X,\omega)$ bajo la acción de $\rm SL(2,\mathbb{R})$ sobre $\Omega^*\mathcal{M}_g$, la siguiente igualdad se satisface en $\rm PSL(2,\mathbb{R})$: $$ \rm Stab(X,\omega) = R \cdot{\rm SL(X,\omega)} \cdot R^{-1} $$ donde $R=(\begin{smallmatrix} -1 & 0\\ 0 & 1 \end{smallmatrix})$. Dado que la geodésica compleja (\ref{E:ComplexGeodesic}) se factoriza al cociente $\mathbb{H}^2/\rm Stab(X,\omega)$, si el grupo de Veech ${\rm SL(X,\omega)}$ es una retícula, entonces, la imagen de dicha geodésica es una curva. La algebricidad puede deducirse de trabajos recientes de Eskin, Mirzakhani [2]A. Eskin, M. Mirzakhani, Invariant and stationary measures for the SL(2,R) action on Moduli space, arXiv:1302.3320 [math.DS]. y Filip [4]S. Filip, Splitting mixed Hodge structures over affine invariant manifolds,arXiv:1311.2350 [math.DS].. Es importante señalar que estos trabajos van más allá del tema de las curvas de Teichmüller: en ellos se logra una descripción de los cerrados invariantes de la $\rm SL(2,\mathbb{R})$-acción sobre el espacio de móduli de superficies planas y, en particular, se prueba que éstos son subvariedades algebraicas.

Volvamos al billar. Diremos que una mesa de billar poligonal $P$ tiene propiedades dinámicas óptimas si el grupo de Veech de la superficie plana $S_P$ asociada es una retícula. Es claro que si $P$ tiene propiedades dinámicas óptimas; entonces, la superficie plana asociada $S_P$ genera una curva de Teichmüller.

Si integramos los resultados anteriores al contexto de los billares, tenemos que hay dos maneras de encontrar mesas con propiedades dinámicas óptimas: bien sea calculando el grupo de Veech de la superficie plana asociada y determinando que es una retícula, o calculando la $\rm SL(2,\mathbb{R})$-órbita de la superficie asociada y determinando que su imagen en $\mathcal{M}_g$ es una curva algebraica. Desgraciadamente, ninguna de las dos posibilidades es sencilla. En los siguientes párrafos concluimos este texto mencionando algunos resultados conocidos.

El grupo de Veech de un billar en un polígono regular con $n\geq 5$ lados es una retícula [16]W. A. Veech, The billiard in a regular polygon, Geom. Funct. Anal., 2 no.3 (1992) 341—379.. En el caso de billares triangulares, podemos considerar los siguientes casos:

1. Triángulos rectos. Un triángulo recto tiene propiedades dinámicas óptimas si y sólo si su ángulo menor es de la forma $\frac{\pi}{n}$ para $n\geq 4$. Esto se deduce de trabajos de Vorobets [17]Ya. B. Vorobets, Plane structures and billiards in rational polygons: the Veech alternative, Uspekhi Mat. Nauk, 51 no. 5(311) (1996) 3—42 (en ruso), Russian Math. Surveys, 51 no. 5 (1996) 779—817. y Kenyon y Smillie [7]R. Kenyon, J. Smillie, Billiards on rational-angled triangles, Comment. Math. Helv., 75 no. 1 (2000) 65—108..
2. Triángulos agudos. Un triángulo agudo isóceles tiene propiedades dinámicas óptimas si y sólo su ángulo distinguido es de la forma $\frac{\pi}{n}$ para $n\geq 3$. Esto también se deduce de los trabajos de Kenyon y Smillie. Por otro lado, los únicos triángulos agudos escalenos que tienen propiedades dinámicas óptimas son aquellos de ángulos interiores: $$ \Bigl(\frac{2\pi}{9},\frac{\pi}{3},\frac{4\pi}{9}\Bigr)\hspace{3mm} \Bigl(\frac{\pi}{4},\frac{\pi}{3},\frac{5\pi}{12}\Bigr)\hspace{3mm} \Bigl(\frac{\pi}{5},\frac{\pi}{3},\frac{7\pi}{15}\Bigr) $$
3. Triángulos obtusos. El siguiente resultado se le debe a W. Veech: un triángulo isóceles con dos ángulos de la forma $\frac{\pi}{n}$, con $n\geq 5$ tiene propiedades dinámicas óptimas. Por otro lado, todo triángulo obtuso escaleno con ángulos interiores $(\frac{\pi}{2n},\frac{\pi}{n},\frac{(2n-3)\pi}{2n})$ tiene también propiedades dinámicas óptimas. Esto se deduce de trabajos de Vorobets [17]Ya. B. Vorobets, Plane structures and billiards in rational polygons: the Veech alternative, Uspekhi Mat. Nauk, 51 no. 5(311) (1996) 3—42 (en ruso), Russian Math. Surveys, 51 no. 5 (1996) 779—817. y Ward [18]C. C. Ward, Calculation of Fuchsian groups associated to billiards in a rational triangle, Ergodic Theory Dynam. Systems, 18 no.4 (1998) 1019—1042..

Aunque ya en 1989, Veech usaba el término de “curva de Teichmüller”, no fue sino hasta la primera década del siglo XXI cuando éstas entraron en su apogeo, debido, en parte, al trabajo de McMullen, Leininger y Möller. El primero, usando técnicas de la geometría algebraica compleja, logró encontrar una familia infinita de curvas de Teichmüller que son generadas por polígonos con forma de $L$. Más precisamente, consideremos la figura 2.

Teorema 3. [11]C. T. McMullen, Billiards and Teichmüller curves on Hilbert modular surfaces, J. Amer. Math. Soc., 16 no. 4 (2003) 857—885..

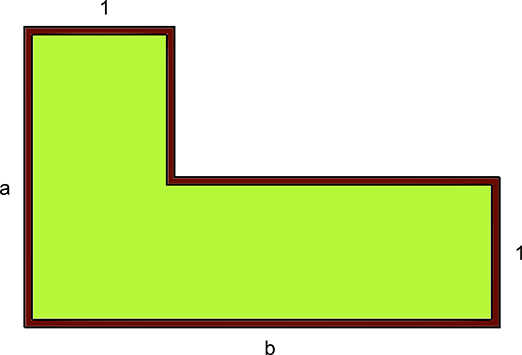
Otros ejemplos de curvas de Teichmüller pueden encontrarse en [10]I. I. Bouw, M. Möller, Teichmüller curves, triangle groups, and Lyapunov exponents, Ann. of Math. (2), 172 no.1 (2010) 139—185., [9]C. J. Leininger, On groups generated by two positive multi-twists: Teichmüller curves and Lehmer's number, Geom. Topol., 8 (2004) 1301—1359. o bien [8]E. Lanneau, D.-M. Nguyen, Teichmüller curves generated by Weierstrass Prym eigenforms in genus 3 and genus 4, J. Topol., 7 no.2 (2014) 475—522.. Sin embargo, el problema general de determinar cuáles superficies planas determinan curvas de Teichmüller sigue abierto. Avances significativos se han logrado en género $g\leq 3$ (ver, por ejemplo, [12]C. T. McMullen, Dynamics of SL_2(R) over moduli space in genus two, Ann. of Math. (2), 165, no.2 (2007) 397—456. o [1]M. Bainbridge, M. Möller, The Deligne-Mumford compactification of the real multiplication locus and Teichmüller curves in genus 3, Acta Math., 208 no. 1 (2012) 1—92.).

Hemos visto que la dinámica del billar en un polígono está emparentada con la dinámica de $\rm SL(2,\mathbb{R})$ sobre el espacio de móduli de superficies planas y las curvas de Teichmüller son el punto de encuentro. Sin embargo, la situación va más allá: la acción del grupo especial lineal sobre $\Omega^*\mathcal{M}_g$ (un espacio no homogéneo) ha demostrado parecerse mucho a la dinámica de grupos lineales sobre espacios homogéneos puesto que la clasificación de cerrados invariantes tiene puntos en comun con la teoría de Ratner (ver [13]C. T. McMullen, The work of Maryam Mirzakhani, http://www-fourier.ujf-grenoble.fr/~lanneau/articles/hdr-lanneau.pdf). Esto último, sin embargo, es parte de otra fenomenología que apenas se está comenzando a entender.

Referencias

[1] M. Bainbridge, M. Möller, The Deligne-Mumford compactification of the real multiplication locus and Teichmüller curves in genus 3, Acta Math., 208 núm. 1 (2012) 1—92.

[2] A. Eskin, M. Mirzakhani, Invariant and stationary measures for the SL(2,R) action on Moduli space, arXiv:1302.3320 [math.DS].

[3] B. Farb, D. Margalit, A primer on mapping class groups, Princeton Mathematical Series 49, Princeton, NJ, 2012.

[4] S. Filip, Splitting mixed Hodge structures over affine invariant manifolds, arXiv:1311.2350 [math.DS].

[5] F. Herrlich, G. Schmithüsen, On the boundary of Teichmüller disks in Teichmüller and in Schottky space, Handbook of Teichmüller theory. Vol. I, IRMA Lect. Math. Theor. Phys. 11, Eur. Math. Soc., Zürich, 2007, 293—349.

[6] P. Hubert, T. A. Schmidt, An introduction to Veech surfaces, Handbook of dynamical systems. Vol. 1B, Elsevier B. V., Amsterdam, 2006, 501—526.

[7] R. Kenyon, J. Smillie, Billiards on rational-angled triangles, Comment. Math. Helv., 75 núm. 1 (2000) 65—108.

[8] E. Lanneau, D.-M. Nguyen, Teichmüller curves generated by Weierstrass Prym eigenforms in genus 3 and genus 4, J. Topol., 7 núm. 2 (2014) 475—522.

[9] C. J. Leininger, On groups generated by two positive multi-twists: Teichmüller curves and Lehmer's number, Geom. Topol., 8 (2004) 1301—1359.

[10] I. I. Bouw, M. Möller, Teichmüller curves, triangle groups, and Lyapunov exponents, Ann. of Math. (2), 172 núm. 1 (2010) 139—185.

[11] C. T. McMullen, Billiards and Teichmüller curves on Hilbert modular surfaces, J. Amer. Math. Soc., 16 núm. 4 (2003) 857—885.

[12] C. T. McMullen, Dynamics of ${\rm SL}_2(\Bbb R)$ over moduli space in genus two, Ann. of Math. (2), 165, núm.2 (2007) 397—456.

[13] C. T. McMullen, The work of Maryam Mirzakhani, http://www-fourier.ujf-grenoble.fr/~lanneau/articles/hdr-lanneau.pdf

[14] M. Möller, Affine groups of flat surfaces, Handbook of Teichmüller theory II, (A. Papadopoulos, editor), IRMA Lectures in Mathematics and Theoretical Physics 13, European Mathematical Society (EMS), 2009, 369—387.

[15] F. Valdez, Billares poligonales y curvas de Teichmüller, universo.math, 1 núm. 2 (2014) artículo 4.

[16] W. A. Veech, The billiard in a regular polygon, Geom. Funct. Anal., 2 núm. 3 (1992) 341—379.

[17] Ya. B. Vorobets, Plane structures and billiards in rational polygons: the Veech alternative, Uspekhi Mat. Nauk, 51 núm. 5(311) (1996) 3—42 (en ruso), Russian Math. Surveys, 51 núm. 5 (1996) 779—817.

[18] C. C. Ward, Calculation of Fuchsian groups associated to billiards in a rational triangle, Ergodic Theory Dynam. Systems, 18 núm. 4 (1998) 1019—1042.