

Este es el primero de dos artículos donde explicaremos la relación que existe entre los billares poligonales y las curvas de Teichmüller.
Muchas veces cuando me preguntan sobre el tema de mis investigaciones suelo responder que, entre otras cosas, me dedico a la teoría matematica de los billares. La respuesta es vaga, pues billares hay muchos. Como muestra basta poner la palabra billiard en MathSciNet y ver el número de resultados encontrados: ¡más de 1200! En los párrafos que siguen hablaremos de billares poligonales y cómo estos están relacionados con una clase muy particular de superficies llamadas superficies planas o de translación. En la segunda parte de este texto trazaremos la conexión entre estas superficies y un tipo particular de curvas algebraicas, a priori muy distantes, las llamadas curvas de Teichmüller. El hilo conductor entre estas tres historias, billares, superficies planas y curvas algebraicas en una acción del grupo lineal especial ${\rm SL}(2,\mathbf{R})$ sobre un espacio móduli... pero no nos adelantemos tanto. Vamos pian pianito.
Al parecer, la mayoría de las mesas de billar en este planeta tiene forma de polígono (de hecho, de un rectángulo). Hay algunas excepciones, como una que se encuentra en la sala de matemáticas del museo UNIVERSUM en la Ciudad de México y tiene forma de elipse. Los llamados billares poligonales son sistemas dinámicos relativamente sencillos que nacen de un modelo muy simple del juego de billar. Este modelo supone lo siguiente:
Recordemos que una trayectoria de billar se dice periódica si la bola que la describe eventualmente regresa a su posición de salida en la misma dirección en la que salió. Según R. E. Schwartz [1]R.E.Schwartz, Obtuse triangular billiards. II. One hundred degrees worth of periodic trajectories, Experiment. Math., 18, no.2 (2009), 137—171., esta conjetura tiene al menos 200 años de antigüedad y se sustenta en el que hecho de que, a grosso modo, sabemos que es cierta para muchos triángulos. Más precisamente, está demostrada para todo triángulo racional, es decir con todos sus ángulos interiores de la forma $\frac{p}{q}\pi$, $(p,q)=1$, y para todo triángulo irracional (es decir, no racional) salvo cuanto éste es un triángulo obtuso con ángulo obtuso mayor a 100 grados. Un lector motivado puede consultar al respecto las monografías [2]H. Masur, S. Tabachnikov, Rational billiards and flat structures, Handbook of dynamical systems, Vol. 1A, North-Holland, Amsterdam, 2002, 1015—1089. y [3]S. Tabachnikov, Geometry and billiards, Student Mathematical Library, 30, American Mathematical Society, Providence, RI, 2005..
Una idea fundamental para estudiar la dinámica de una trayectoria de billar en un polígono $P$ consiste en asociarle a éste una superficie plana $S_{P}$ junto con una proyección $\pi_{P}:S_{P}\to P$ que mande geodésicas en $S_{P}$ sobre trayectorias de billar. Una geodésica en nuestro contexto, como veremos más adelante, es una curva en $S_{P}$ formada por segmentos paralelos a una misma dirección. Explicaremos primero cómo construir $S_{P}$ y después lo que queremos decir por plana. La construcción que estamos por presentar tiene como pieza fundamental a un polígono euclidiano $P$ y como resultado un conjunto $S_{P}$ que, salvo por algunos puntos ``problemáticos'', es tan plano como el plano euclidiano. La construcción fue propuesta primero por Fox y Kershner [4]R.H. Fox, R.B. Kershner, Concerning the transitive properties of geodesics on a rational polyhedron, Duke Math. J., 2, no. 1 (1936), 147—150. a principios del siglo XX y redescubierta en los años setenta por A. B. Katok y A. N. Zemljakov [5]A.N. Zemljakov, A.B. Katok, Topological transitivity of billiards in polygons (Russian), Mat. Zametki, 18, no.2 (1975), 291—300.. Ilustramos los aspectos generales de ésta en los siguientes párrafos.
Tomemos $P$ un polígono euclidiano de lados $\{e_{1},\ldots,e_{n}\}$ y ángulos interiores $\{\alpha_{1},\cdots,\alpha_{n}\}$. Sea $\sigma_{i}$ la reflexión del plano con respecto a la recta que contiene al lado $e_{i}$. Definimos $H < Isom(\mathbf{R}^{2})$ como el grupo generado por las isometrías del plano $\{\sigma_{1},\ldots,\sigma_{n}\}$. La multiplicación dentro de $H$ se realiza por la izquierda. Consideremos la familia de copias de $P$:
\begin{equation} \label{E:P} \mathcal{P}:=\bigsqcup_{h\in H}P\times h \end{equation}Sobre $\mathcal{P}$ definimos dos identificaciones de manera intuitiva:
Al conjunto que resulta de aplicar sobre $\mathcal{P}$ las dos identificaciones anteriores lo denotamos por $S_{P}$. Esta construcción nace de la siguiente observación elemental: si en lugar de reflejar la trayectoria al momento de una colisión reflejamos la mesa entonces la continuación natural de la trayectoria en la mesa reflejada define un segmento de línea recta. Esta frase queda ilustrada en la figura 1.
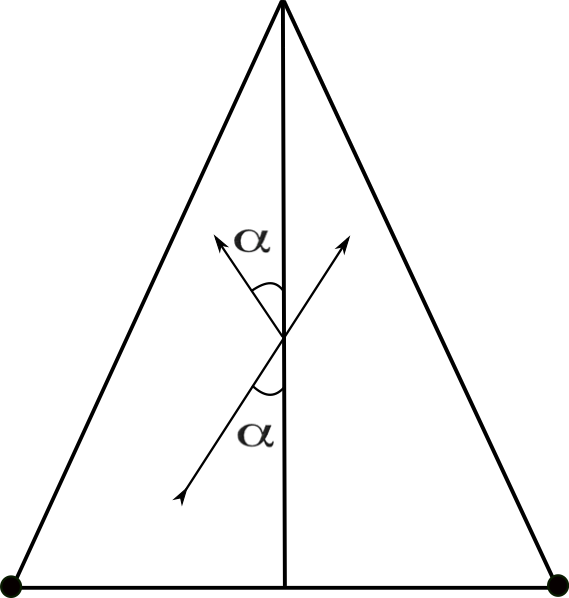
Nótese que, por construcción, existe una proyección natural \begin{equation} \label{e:proj} \pi_{P}:S_{P}\to P \end{equation} Este conjunto, cuando $P$ es un polígono racional, admite una estructura de superficie de Riemann compacta y sin frontera cuya topología está completamente determinada por los ángulos interiores del polígono. Por ejemplo consideremos el caso cuando $P$ es un cuadrado. En la figura 2, ilustramos la primera de las identificaciones que acabamos de definir, cuando la trayectoria de la pelota rebota en el lado etiquetado con la letra B.
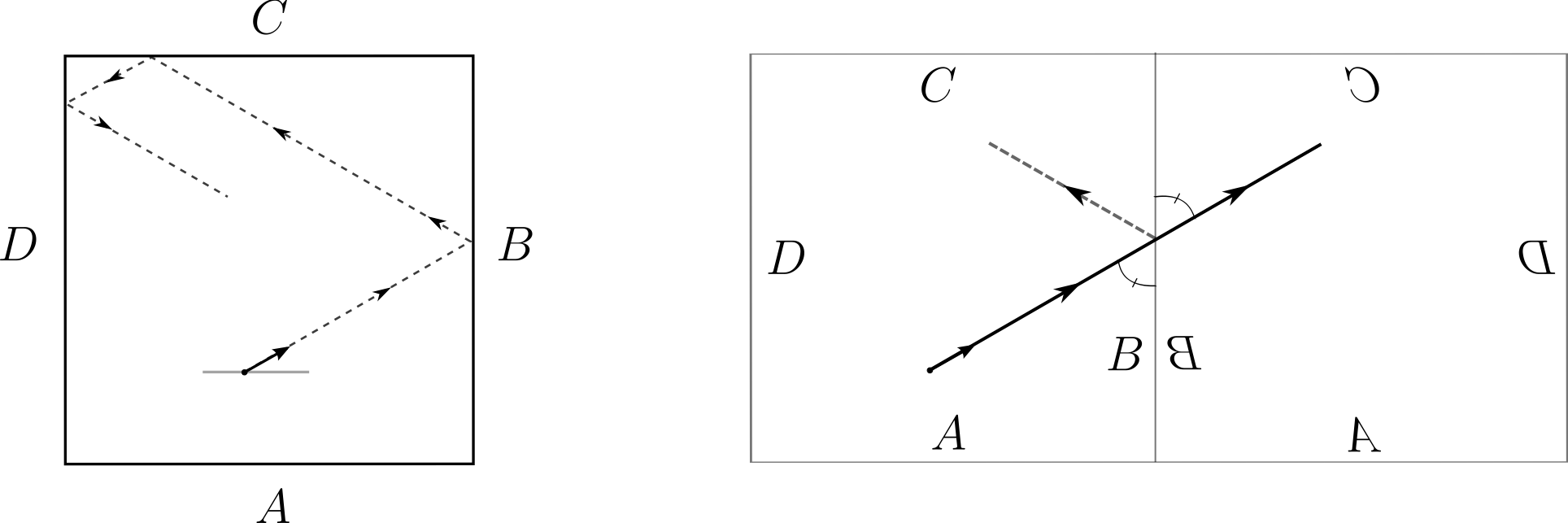
Del lado derecho de la figura 2 vemos entonces dos cuadrados identificados a lo largo del lado B. Si reflejáramos una vez más en la dirección horizontal, obtendríamos un cuadrado que difiere del cuadrado ``original'' con el que comenzamos por una translación horizontal. Lo mismo sucedería si procedemos con estas identificaciones en la dirección vertical.

Al hacer todas las identificaciones posibles, como queda ilustrado en la figura 3, obtenemos un cuadrado formado por cuatro copias de nuestro cuadrado original donde lados opuestos se identifican usando translaciones. La figura 3 ilustra también cómo en este caso la superficie $S_{P}$ obtenida es en realidad un toro. Un lector curioso puede verificar que el mismo fenómeno ocurre cuando $P$ es un triángulo equilátero, salvo que no obtenemos exactamente el mismo toro plano. En la figura 4 ilustramos la construcción de la superficie $S_{P}$ cuando $P$ es un triángulo de ángulos interiores $(\frac{\pi}{8},\frac{3\pi}{8})$.
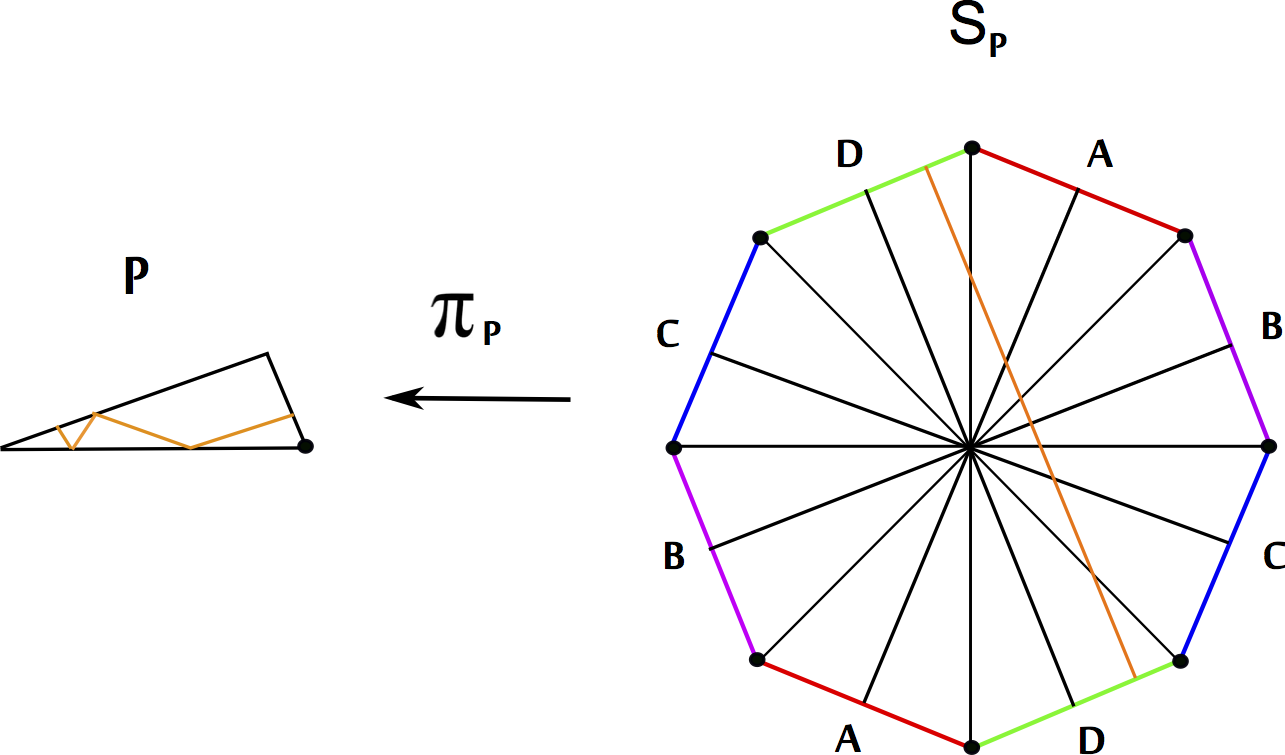
Observemos cómo el octágono en la figura anterior presenta un punto distinguido. Éste punto es diferente del resto dado que vecindades suficientemente pequeñas de éste ya no son isométricas a abiertos del plano. En la ocurrencia, las vecindades en cuestión definen un cubriente 3 a 1 ramificado de una vecidad del origen en el plano. Estamos ante una singularidad cónica de ángulo total $6\pi$. Éste tipo de puntos especiales tienen como génesis vértices de $P$ donde el ángulo interior no es de la forma $\frac{\pi}{n}$ con $n\in\mathbb{N}$.
De ahora en adelante consideraremos polígonos racionales, que recordemos son aquéllos cuyos ángulos interiores son todos conmesurables con $\pi$. En este contexto $S_{P}$ admite siempre una estructura de superficie de Riemann compacta. Más precisamente:
Para polígonos racionales, la superficie $S_{P}$ está naturalmente triangulada por un número finito de copias de $P$ y es posible sustraerle un subconjunto discreto $\Sigma$ de manera que $S(P)\setminus \Sigma$ tenga una métrica plana. En efecto, $\Sigma$ corresponde al conjunto de vértices en la triangulación definida por $P$ donde el ángulo interior no es de la forma $\frac{\pi}{n}$. Por la segunda regla que usamos en la construcción anteriormente descrita $S_{P}\setminus \Sigma$ es una superficie de translación, es decir, una donde los cambios de coordenadas son translaciones del plano. Entonces podemos tomar la ``imagen inversa'' de la métrica estándar del plano, que es invariante por translaciones, y obtenemos una métrica de curvatura cero sobre $S_{P}\setminus \Sigma$. Es en éste sentido que decimos, abusando del lenguaje, que $S_{P}$ es plana. Los puntos de $\Sigma$ son las llamadas singularidades cónicas de la superficie. La superficie $S_{P}$ es el prototipo de lo que se conoce como una superficie de translación o superficie plana. La definición general es presentada a continuación.
Como en el caso de $S_{P}$, los puntos del subconjunto discreto $\Sigma$ se llaman singularidades cónicas. Esta nomenclatura se justifica pues la superficie $S\setminus\Sigma$ admite una métrica plana y existen vecindades de los puntos de $\Sigma$ que son isométricas a un cubriente finito ramificado de una vecindad del origen en el plano. Diremos que una singularidad cónica es de ángulo total $2\pi k$, con $k\in\mathbb{N}$, si el cubriente ramificado en cuestión tiene una fibra genérica de cardinalidad $k$.
Si $S$ es una superficie plana, entonces el haz tangente de $S':=S\setminus\Sigma$ es trivial, es decir, está dado por el producto $S'\times\mathbb{R}^{2}$. Esto es una simple consecuencia de que los cambios de coordenadas en $S'$ tengan derivada igual a la identidad. Esto es sumamente conveniente pues nos permite descomponer también al haz tangente unitario como un producto $T^{1}S'=S'\times(\mathbb{R}/2\pi\mathbb{Z})$, y para cada dirección $\theta\in{R}/2\pi\mathbb{Z}$ considerar el campo de vectores paralelos $X_{\theta}:=\rho^{-1}(\theta)$, donde $\rho:S'\times(\mathbb{R}/2\pi\mathbb{Z})\to\mathbb{R}/2\pi\mathbb{Z}$ es la proyección en el segundo factor. Cada curva integral maximal de $X_{\theta}$ será llamada una geodésica paralela a la dirección $\theta$ y al flujo (a veces local, es decir no definido para todo tiempo) de dicho campo se le llamará el flujo geodésico en la dirección $\theta$. Lo denotaremos por $g^{t}_{\theta}$. La nomenclartura viene del hecho de que estas nociones coinciden con las estándares en geometría diferencial cuando consideramos la métrica plana natural sobre la superficie de translación $S$. No es difícil ver que en el caso de que $S=S_{P}$ provenga de un billar, toda geodésica se proyecta, vía $\pi_{P}$ (ver \ref{e:proj}) en una trayectoria de billar y toda trayectoria de billar es imagen vía $\pi_{P}$ de una geodésica.
En resumen, hemos transformado el problema de estudiar la dinámica de la bola de billar en el problema de estudiar el flujo geodésico en la superficie plana $S_{P}$.
La idea ahora es inscribir a las superficies planas en un contexto analítico. Para esto veremos que la siguiente definición es equivalente a la Definición 1.
Supongamos que $X$ es compacta y sin frontera. Toda 1-forma holomorfa se escribe localmente como $f(z)dz$ donde $f(z)$ es una función holomorfa y $dz=dx+idy$. Definamos $Z(\omega)$ como el conjunto de ceros de la forma $\omega$ y $X'=X\setminus Z(\omega)$. Entonces, para cada $p_{0}\in X'$ podemos definir la carta \begin{equation} \label{trol} z(p)=\int_{p_{0}}^{p}\omega \end{equation} en una vecindad de $p$ cercanas a $p_{0}$. Nótese que en la coordenada $z$ tenemos que $\omega=dz$. Obsérvese que si cambiamos ``punto base'' ($p_{0}$ por un $q_{0}$ cercano) entonces las cartas coordenadas cambian por una translación. En efecto: \begin{equation} c:=\int_{p_{0}}^{p}\omega-\int_{q_{0}}^{p}\omega=\int_{p_{0}}^{q_{0}}\omega \end{equation} donde $c$ es una constante que no depende de $p$. Ergo, los cambios de coordenadas en la estructura definida por las cartas (\ref{trol}) son todos de la forma $z\to z+c$, es decir, translaciones. En una vecindad de un punto $p\in Z(\omega)$, la forma $\omega$ se escribe como $z^{k}dz$, por lo que $z(p)$ es una función de la forma $p\to p^{k+1}$ lo que implica que el atlas definido por \ref{trol} se extiende a $p$ y en este punto aparece una singularidad cónica de ángulo total $2\pi(k+1)$.
Conversamente, toda superficie plana $S$ que satisfaga la Definición 1 puede ser vista como una pareja $(X,\omega)$. Para ello basta considerar la ``imagen inversa'' vía cualquier carta de $S\setminus \Sigma$ de la 1-forma estándar invariante por translaciones $dz$ en $\mathbb{C}$ y luego extender ésta a $\Sigma$ de manera analítica.
Este nuevo punto de vista, que por obvias razones llamaremos analítico, nos permite ver a las superficies planas como puntos de un haz bastante conocido. En efecto, sea $\mathcal{M}_{g}$ el espacio de móduli de superficies de Riemann compactas, conexas y sin frontera de género $g$. Entonces si $X$ es este tipo de superficie de Riemann tenemos que $(X,\omega)\in\Omega^{*}\mathcal{M}_{g}$, donde $\Omega^{*}\mathcal{M}_{g}$ es el haz vectorial de 1-formas holomorfas sobre $\mathcal{M}_{g}$. Llamaremos a $\Omega^{*}\mathcal{M}_{g}$ el espacio móduli de superficie planas de género $g$.
Recordemos que dada una 1-forma holomorfa $\omega$ sobre una superficie de Riemann $X$ de género $g$ su conjunto de zeros $Z(\omega)=\{p_{1},\ldots,p_{n}\}$ es finito y si $p_{i}$ es cero de multiplicidad $m_{i}$ entonces:
\begin{equation} \sum_{i=1}^{n}m_{i}=2g-2. \end{equation}Esta fórmula puede deducirse del teorema de Riemann-Roch, por ejemplo. Lo importante de este hecho es que nos dice que el espacio de móduli de superficies planas $\Omega^{*}\mathcal{M}_{g}$ se descompone naturalmente en subconjuntos que corresponden a fijar el número y multiplicidad de los ceros $\omega$. A cada uno de estos subconjuntos se les conoce como estratos y los denotaremos como $\mathcal{H}(m_{1},\ldots,m_{n})$. Así las cosas, por ejemplo, tenemos que $\Omega^{*}\mathcal{M}_{2}=\mathcal{H}(1,1)\sqcup\mathcal{H}(2)$ y $$ \Omega^{*}\mathcal{M}_{3}=\mathcal{H}(4)\sqcup\mathcal{H}(3,1)\sqcup\mathcal{H}(2,2)\sqcup \mathcal{H}(2,1,1)\sqcup\mathcal{H}(1,1,1,1). $$ Cada estrato $\mathcal{H}(m_{1},\ldots,m_{n})$ es un orbifold con estructura compleja (fuera de los puntos de orbifold) y además: $$ {\rm dim}_{\mathbb{C}}\mathcal{H}(m_{1},\ldots,m_{n})=2g+m-1. $$ Quizás aún más sorprendente es que estos estratos no son subconjuntos conexos de $\Omega^{*}\mathcal{M}_{g}$. La clasificación completa de las componentes conexas es un trabajo fundamental de M. Kontsevich y A. Zorich [6]M. Kontsevich, A. Zorich, Connected components of the moduli spaces of Abelian differentials with prescribed singularities, Invent. Math., 153, no.3 (2003), 631—678..
En la segunda parte de este texto, que aparecerá en el número siguiente, definiremos una acción de ${\rm SL}_{2}(\mathbb{R})$ sobre $\Omega^{*}\mathcal{M}_{g}$. En términos generales, si consideramos la proyección natural $\Omega^{*}\mathcal{M}_{g}\to\mathcal{M}_{g}$ enviará las órbitas de dicha acción en subconjuntos del espacio de móduli $\mathcal{M}_{g}$ que en casos muy particulares, serán curvas algebraicas. Estos casos particulares ocurren por ejemplo cuando la superficie plana en cuestión proviene de una mesa de billar con muchas simetrías, como la de la figura 2. Lo más sorprendente de esta imagen, es que cuando en efecto las órbitas antes mencionadas se proyectan en curvas algebraicas entonces podemos describir en su totalidad la dinámica del billar.
To be continued...
[1] R.E.Schwartz, Obtuse triangular billiards. II. One hundred degrees worth of periodic trajectories, Experiment. Math., 18, no.2 (2009), 137—171.
[2] H. Masur, S. Tabachnikov, Rational billiards and flat structures, Handbook of dynamical systems, Vol. 1A, North-Holland, Amsterdam, 2002, 1015—1089.
[3] S. Tabachnikov, Geometry and billiards, Student Mathematical Library, 30, American Mathematical Society, Providence, RI, 2005.
[4] R.H. Fox, R.B. Kershner, Concerning the transitive properties of geodesics on a rational polyhedron, Duke Math. J., 2, no. 1 (1936), 147—150.
[5] A.N. Zemljakov, A.B. Katok, Topological transitivity of billiards in polygons (Russian), Mat. Zametki, 18, no.2 (1975), 291—300.
[6] M. Kontsevich, A. Zorich, Connected components of the moduli spaces of Abelian differentials with prescribed singularities, Invent. Math., 153, no.3 (2003), 631—678.
