Sólo hablaremos del cubo de Rubik clásico, de orden $3\times3\times3$, dejando al lado los múltiples variantes en cuanto a forma y complejidad que se han ingeniado a raíz del invento original de Ernő Rubik en 1974. Tanto se ha escrito acerca de este juego que sobraría describir en detalle su mecanismo o las reglas del problema.
Presentaremos aquí una solución al problema de armar el cubo a partir de cualquier posición de la cual sea posible hacerlo. Esto irá junto con una demostración matemática de que el método sí funciona, basada en los conceptos elementales de las acciones de los grupos sobre los conjuntos. Si le apura al lector encontrar un método para ganar campeonatos mediante una solución con un número mínimo de vueltas de las caras del cubo, será mejor que busque en otra parte. El presente método es más bien “lento y seguro”, pero creo que tiene algunas características interesantes. Aparte de ser instructivo desde la perspectiva de la teoría de grupos, creo que los movimientos son relativamente fáciles de recordar durante largos períodos sin tocar un cubo. Los movimientos elementales son cortos y simétricos, y un mismo movimiento puede servir en distintas etapas de la solución. También el presente enfoque conlleva intrínsecamente mucha flexibilidad: señalaremos cómo el aficionado puede descubrir alternativas para ciertos pasos e irlos agregando a su repertorio para mejorar su tiempo. Por lo general, tardo como dos minutos en resolverlo.
Daremos por sentadas las nociones de grupo y homomorfismo de grupos [4]En Wikipedia, “Grupo (matemática)”. y resumimos aquí un poco de terminología estándar [3]En Wikipedia, “Acción (matemática)”. para la acción de un grupo $G$ sobre un conjunto $A.$
El grupo de permutaciones de $A$, llamado también el grupo simétrico sobre $A$, es \[ \mathcal{S}(A) = \{ g\colon A\to A\ |\ g \mbox{ es una biyección} \} \] con composición de funciones como la operación de grupo.
Consideremos un subgrupo $G\subseteq \mathcal{S}(A)$. Un subconjunto $A_0\subseteq A$ se llama $G$-invariante cuando $g(A_0)=A_0$ para todo $g\in G$. Aquí $g(A_0)=\{g(a)\ | \ a\in A_0\}$ es la imagen de $A_0$ bajo $g$. Por otra parte, una función $\phi\colon A\to B$ de $A$ en un conjunto $B$ cualquiera se llama $G$-invariante cuando $\phi(g(a))=\phi(a)$ para todo elemento $a\in A$ y todo $g\in G$, o sea $\phi\circ h=\phi.$
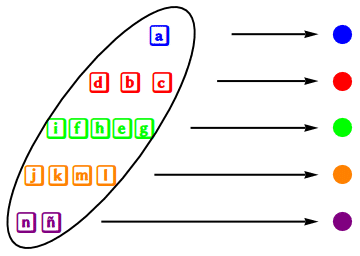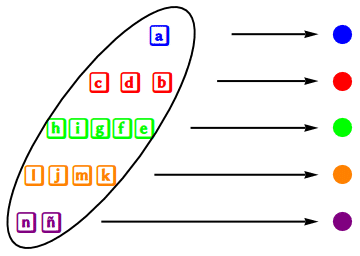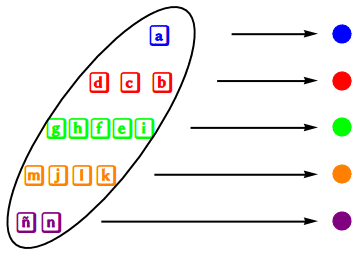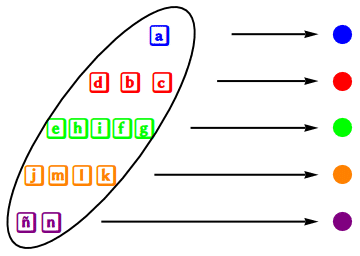
La órbita de un elemento $a\in A$ bajo la acción de $G$ es la colección $\{g(a)\ | \ g\in G\}$. Cuando hay un solo órbita (igual a todo $A$), se dice que la acción es transitiva. Un punto fijo de $g$ es un elemento $a\in A$ tal que $g(a)=a$ (equivalentemente, $\{a\}$ es invariante bajo el subgrupo cíclico de $G$ generado por $g$.) Mas generalmente, $a$ es un punto periódico de periodo $n$ cuando $g^n(a)=a$; es decir, $a$ es un punto fijo de la potencia por composición $g^n$. El estabilizador $G_a$ de un punto $a\in A$ es el subgrupo de elementos que tienen a $a$ como punto fijo común, \[ G_a = \{ g\in G\ | \ g(a)=a \}. \] De manera similar, el estabilizador de un subconjunto $A'\subseteq A$ es $G_{A'}=\{g\in G\ | \ g(A')\subseteq A'\}$. Cuando $b=h(a)$ con $h\in G$, $a\in A$, el estabilizador de $b$ puede calcularse en términos del de $a$ por la relación \[ G_b = hG_ah^{-1} . \] Este subgrupo es el conjunto de conjugados $hgh^{-1}$ de elementos de $G_a$. Es útil notar la relación entre propiedades de un elemento o subgrupo de $G$, y las que le corresponden bajo la conjugación. Por ejemplo, si $a$ es un punto fijo de $g$, entonces $h(a)$ es un punto fijo de $hgh^{-1}$. Otra construcción importante es el conmutador \[ [g,h] = ghg^{-1}h^{-1} \] que sería la identidad de grupo si $G$ fuera conmutativo; y si no, por lo que de alguna manera sirve para detectar qué tanto $G$ no es conmutativo.
Una función $G$-invariante es simplemente una que es constante en cada órbita. Decimos que $\phi\colon A\to B$ es un invariante completo para la acción de $G$ en $A$ si $\phi(a_1)=\phi(a_2)$ precisamente cuando $a_1$, $a_2$ están en la misma órbita. En particular, para un invariante completo, $\phi(a_1)=\phi(a_2)$ implica que existe algún elemento $g\in G$ tal que $g(a_1)=a_2$. La cuestión de la existencia de este tipo de elemento es, de hecho, el tema de este trabajo.
Dado que solamente nos van a interesar acciones de grupos finitos sobre conjuntos finitos, es el momento de decir que el número de elementos de $\mathcal{S}(A)$ es el factorial del número de elementos de $A$, \[ \#\mathcal{S}(A) = (\#A)! \]
La noción de acción de grupo se extiende de manera natural a la situación en que $G$ no es necesariamente un subgrupo de $\mathcal{S}(A)$, sino que consideramos un homomorfismo de grupos $T\colon G\to\mathcal{S}(A)$, que se puede escribir $T\mapsto T_g$. Las nociones de órbita, estabilizador, etc., correspondientes a $G$ se obtienen aplicando la transformación $T_g$ en lugar de $g$ en las descripciones dadas arriba. Cuando $H$ es un subgrupo de $G$, la acción de $G$ en $A$ induce una acción de $H$ en $A$ por restricción, es decir, $T_h$ para $h\in H$ es simplemente $T_h$ considerando $h$ como elemento de $G$.
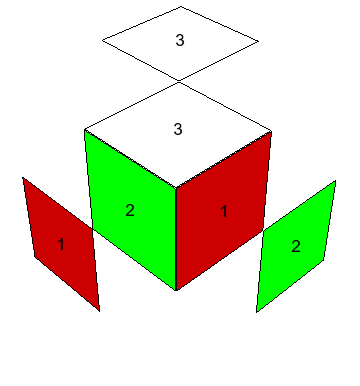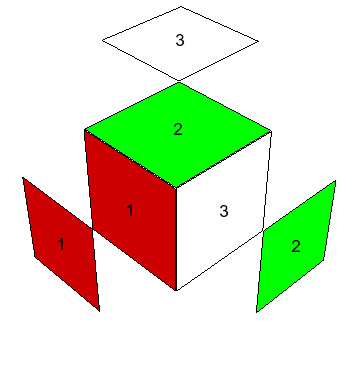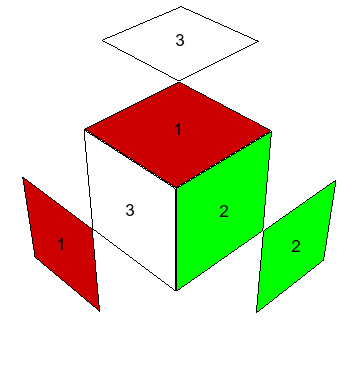
Al mirar directamente hacia cualquiera de las seis caras del cubo $3\times3\times3$, vemos nueve de los 26 cubitos visibles, o sea, la cara tiene nueve caritas: uno en el centro, cuatro en aristas y cuatro en esquinas (o vértices). Estos tres tipos de cubitos se distinguen por ser compartidos entre una, dos y tres caras del cubo respectivamente. Así las esquinas tienen tres caritas visibles hacia afuera, las aristas dos. Considerando los centros de las caras como armados en posición relativa rígida y fija, nos preocupamos solamente de cómo se mueven las esquinas y las aristas con respecto a los centros. Escribiremos $\mbox{Cub}_3$ y $\mbox{Cub}_2$ para los conjuntos de esquinas y aristas, respectivamente.
Los movimientos básicos. Haciendo caso omiso —pero sin despreciar— de las diversas notaciones que se han vuelto más o menos estándar en el mundo de Rubik, voy a describir las partes del cubo como sigue. La cara más cercana a mí se llamará “X”; la cara a mi derecha se llamará “Y”, y la de arriba, “Z“. Lo hago así porque algunos de mis lectores quizás no conozcan las otras notaciones, mientras que la mayoría de los que hayan estudiado algo de matemáticas reconocerán una forma tradicional de etiquetar los ejes de un sistema de coordenadas tridimensional. Estas caras se llamarán también $X^+$, $Y^+$, $Z^+$ para énfasis, y las caras respectivas opuestas a ellas (y más lejanas de mí) serán $X^-$, $Y^-$, $Z^-$. Generalmente sostengo el cubo con la cara $Y^-$ en la mano izquierda, de manera que, con la derecha, pueda rotar fácilmente $X$, $Y$, $Z$. Las rotaciones de las seis caras por un cuarto de vuelta ($90^\circ)$ en el sentido de las manecillas del reloj serán indicadas por minúsculas: $x=x_+$, $y=y_+$, $z=z_+$, $x_-$, $y_-$, $z_-$; aclaro que el sentido horario es desde la perspectiva de alguien que esté mirando la cara misma (en muchos lugares estos cuartos de vuelta se escriben $F,R,U,B,L,D$.) Los zurdos pueden intercambiar las definiciones de $y_+$, $y_-$ y seguir adelante plácidamente.
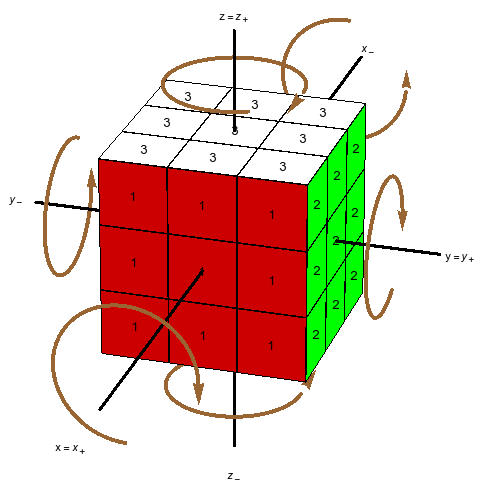
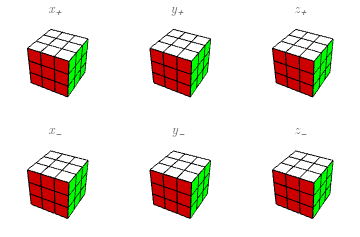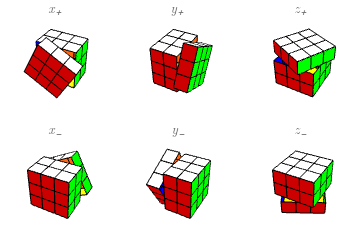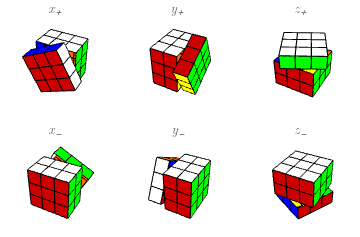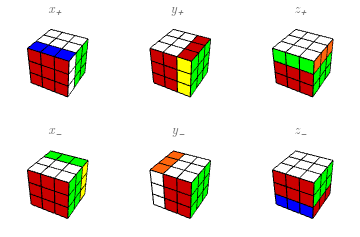
Siguiendo la notación tradicional, una aplicación de sucesivas rotaciones se escribirá de izquierda a derecha: así $xy$ significa aplicar primero $x$, luego $y$. Cuando dos o más rotaciones consecutivas son iguales, se pueden combinar en una sola, llevando un exponente que indique cuántas son; un exponente negativo indica que la rotación va en el sentido contrario. Así \[ xx=x^2,\quad xx^{-1}=\mathbf{1}, \ \] etc., donde $\mathbf{1}$ significa que no mueve ningún cubito.
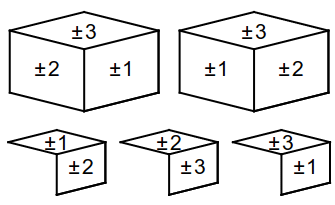
Los colores. Tenemos que hablar de colores también: cuando el cubo está resuelto, lo cual llamaremos la configuración original, las caras $X$, $Y$, $Z$, $X^-$, $Y^-$, $Z^-$ muestran cada una un sólo color; los seis colores distintos se llamarán $1$, $2$, $3$, $-1$, $-2$, $-3$ respectivamente. Cada centro se identifica por su color, mientras los 12 cubitos arista ostentan los respectivos colores \[ (1,2),\ (1,-2),\ (-1,2),\ (-1,-2), \] \[ (1,3),\ (1,-3),\ (-1,3),\ (-1,-3), \] \[ (2,3),\ (2,-3),\ (-2,3),\ (-2,-3). \] y los 8 cubitos esquina llevan los colores \[ (1,2,3),\ (1,-2,-3),\ (-1,2,-3),\ (-1,-2,3), \] \[ (-1,-2,-3),\ (1,2,-3),\ (1,-2,3),\ (-1,2,3); \] Los renglones señalados arriba particionan $\mbox{Cub}_2$ y $\mbox{Cub}_3$ en conjuntos que tendrán gran importancia en el análisis del problema. Las habitaciones respectivas de estos cubitos, es decir los lugares en que se encuentran en la configuración inicial, se pueden denotar cómodamente indicando las intersecciones de tres caras para esquinas y las de dos caras para aristas: \[ XY,\ XY^-,\ X^-Y,\ X^-Y^-, \] \[ XZ,\ XZ^-,\ X^-Z,\ X^-Z^-, \] \[ YZ,\ YZ^-,\ Y^-Z,\ Y^-Z^-. \] \[ XYZ,\ XY^-Z^-,\ X^-YZ^-,\ X^-Y^-Z, \] \[ X^-Y^-Z^-,\ XYZ^-,\ XY^-Z,\ X^-YZ; \] Escribiremos $\mbox{Hab}_2$, $\mbox{Hab}_3$ para los conjuntos de habitaciones de aristas y de esquinas, también de 12 y 8 elementos, respectivamente. Los renglones particionan estos conjuntos en lo que llamaré las tres casas de las aristas y las dos casas de las esquinas. Un cubito está en casa cuando está colocado en una de las habitaciones de su propia casa, y se encuentra, como quien dice, de visita cuando no esté en casa.
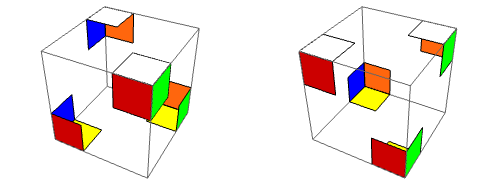
Los estados. La colección de todos los estados del cubo, o sea las formas de colocar los 20 cubitos arista y esquina alrededor de los centros fijos, se llamará $E$. No nos importa impresionar al lector con cuántos estados hay en $E$ (este número aparece en casi cualquier estudio del cubo de Rubik), pero no podemos resistir la observación que el número de posiciones en un problema dado no necesariamente tiene relación con la dificultad. Las reglas del juego también son esenciales en determinar la dificultad de solución. Por ejemplo, si alguien coloca $n$ fichas numeradas del 1 al $n$ en una línea en orden aleatorio y nos toca ordenarlas de forma creciente intercambiando pares de fichas tantas veces como queramos, cualquiera descubre la solución en un momento: no requiere más de $n-1$ intercambios. Pero este juego, aunque trivial de resolver, tiene para $n=20$ muchísimos más estados que el cubo de Rubik, y su grupo de movimientos también es muchísimo más grande.
¿Cómo definir el conjunto $E$ de estados con rigor matemático? Para las esquinas, consideremos la colección $\mathcal{C}_3$ de todas las formas de escoger tres colores, es decir, todos los triples ordenados de colores $(a,b,c)$ donde $a,b,c\in\{\pm1,\pm2,\pm3\}$, y los valores absolutos $|a|$, $|b|$, $|c|$ son distintos. De manera similar, definimos $\mathcal{C}_2$ como la colección de todos los pares $(a,b)$ con $a,b\in\{\pm1,\pm2,\pm3\}$, y los valores absolutos $|a|$, $|b|$ distintos. Debe quedar claro que $\mathcal{C}_2$, $\mathcal{C}_3$ son conjuntos más grandes que $\mbox{Cub}_2$, $\mbox{Cub}_3$, de hecho, tenemos proyecciones $\mathcal{C}_2\to\mbox{Cub}_2$, $\mathcal{C}_3\to\mbox{Cub}_3$ que ordenan las entradas con sus valores absolutos crecientes.
Ahora podemos definir un estado del cubo de Rubik como una función \[ e\colon \mbox{Hab}_2 \cup \mbox{Hab}_3 \to \mathcal{C}_2 \cup \mathcal{C}_3 \] con ciertas restricciones. En primer lugar, $e$ debe enviar elementos de $\mbox{Hab}_2$ en $\mathcal{C}_2$ y elementos de $\mbox{Hab}_3$ en $\mathcal{C}_3$. El valor de $e$ para una habitación determinada representará cuál cubito está colocado en esa habitación y también cómo está orientada, por medio del color en la cara correspondiente del nombre de la habitación. Por ejemplo, la condición \[ e(X^-YZ^-) = (-2,-3,1) \] significa que la esquina $(1,-2,-3)\in\mbox{Cub}_3$ está colocada en la habitación $X^-YZ^-$, con el color $-2$ en la cara $X^-$, el color $-3$ en la cara $Y$ y el color $1$ en la cara $Z^-$. Sin embargo, una tal asignación no puede hacerse de manera arbitraria: por ejemplo, es imposible tener $e(X^-YZ^-)=(1,-3,2)$ porque las caritas de la esquina $(1,2,-3)$, cuya habitación original es $XYZ^-$, llevan los colores $1,2,-3$ en el sentido contrario a las manecillas del reloj, contradiciendo la interpretación de la fórmula propuesta como $1$ en $X^-$, $2$ en $Z^-$, $-3$ en $Y$, que van en sentido antihorario (no hay dos esquinas que sean imágenes especulares una de la otra.) Así la segunda condición para $e$ puede expresarse de la siguiente forma: para cualquier posición $p\in\mbox{Hab}_3$, el orden cíclico de los colores en $e(p)\in\mathcal{C}_3$ tiene que ser el mismo orden cíclico que en el cubito que tiene los colores $e(p)$, en caso de que esta esquina esté en casa en $p$, y en el orden cíclico opuesto cuando esté de visita (para aristas, no ponemos ninguna condición análoga.) La tercera y última condición para que $e$ sea un estado es que todos los cubitos esquinas y aristas deben aparecer representadas una y una sola vez en la imagen de $e$: la composición de $e$ con las proyecciones de $\mathcal{C}_2$, $\mathcal{C}_3$ produce biyecciones a $\mbox{Cub}_2$, $\mbox{Cub}_3$. Así, $E$ es la colección de todas las funciones $e$ que satisfacen estas tres condiciones.
Con esta terminología establecida, el estado original, que llamaremos $e_0$, es la función que asigna a cada cubito a su colocación original, $e_0(XYZ)=(1,2,3)$, $e_0(XY)=(1,2)$, $e_0(X^-YZ)=(-1,2,3)$, etc.
Los bicolores. Tendremos que pensar también en lo que llamo los bicolores: en mi cubo, los colores opuestos son algo similares, y cuando se baja la luz ambiente un poco, ya no los alcanzo a distinguir. Los dos colores $1$, $-1$ colectivamente serán el bicolor $\pm1$, y similarmente hay dos otros bicolores $\pm2$, $\pm3$ para los pares restantes de colores opuestos. Cada esquina lleva todos los tres bicolores, pero no por eso son todas ellas idénticas en bicolores: las esquinas de una casa llevan los bicolores en el orden cíclico opuesto a las de la otra. A cada arista le falta un bicolor; nuevamente la bicoloración es idéntica dentro de cada casa. Tanto para esquinas como para aristas, las casas se podrían haber definido como las clases de equivalencia cuando se pasa de colores a bicolores.
El conjunto $\tilde E$ de estados de cubo de Rubik a bicolores se define de manera análoga al del cubo a colores. Un elemento de $\tilde E$ es \[ \tilde e \colon \mbox{Hab}_2 \cup \mbox{Hab}_3 \to \tilde{\mathcal{C}}_2 \cup \tilde{\mathcal{C}}_3 \] donde $\tilde{\mathcal{C}}_2$, $\tilde{\mathcal{C}_3}$ se definen al reemplazar los colores $1$, $2$, $3$, $-1$, $-2$, $-3$ por los bicolores $\pm1,\pm2,\pm3$ correspondientes en $\mathcal{C}_2$, $\mathcal{C}_3$ (naturalmente eliminando duplicaciones), y restringiéndonos a aquellas funciones $\tilde e$ que pueden obtenerse de elementos $e\in E$ por esta relación.
Hay una proyección natural \[ \pi\colon E\to \tilde E \] que envía cada estado $e\in E$ al estado $\tilde e=\pi(e)\in\tilde E$ que se define al reemplazar los colores con bicolores (en palabras más intuitivas, $\pi$ se realiza “bajando la luz”.) El estado original en $\tilde E$ es $\tilde e_0=\pi(e_0)$.
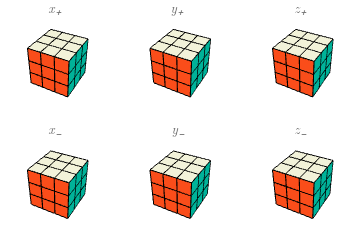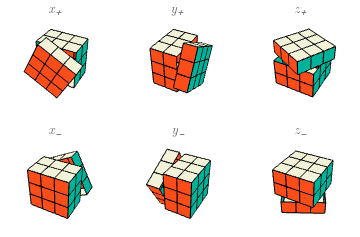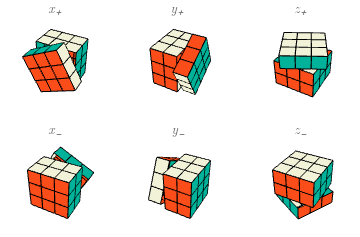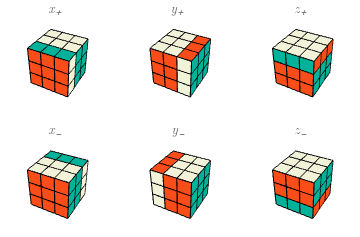
El número de elementos del grupo simétrico $\mathcal{S}(E)$ es bastante grande: el factorial del número del elementos de $E$. El grupo de movimientos $G\subseteq\mathcal{S}(E)$ de cubo de Rubik es un subgrupo muy especial, a veces llamado el grupo de Rubik. De hecho, veremos que $\#G<\#E$.
Para definir la acción, primero consideremos la rotación $x$ de la cara más cercana mí, que revuelve los cubitos de la cara $X$ y deja en sus lugares los demás cubitos. Dado cualquier estado $e\in E$, formamos un nuevo estado $T_x(e)$ por la regla de que $T_x(e)(p)=e(p)$ para las posiciones $p$ afuera de la cara $X$, mientras que, para $p$ en la cara $X$, tomamos en cuenta que la rotación mueve cada una de las caritas en $Y^\pm$ a una carita en $Z^\pm$, y viceversa, conservando la carita en $X$. Específicamente, cuando $p$ es posición arista, \begin{eqnarray*} T_x(e)(XY) = e(XZ),\ && T_x(e)(XY^-)=e(XZ^-), \\ T_x(e)(XZ)=e(XY^-),\ && T_x(e)(XZ^-)=e(XY); \end{eqnarray*} mientras que, cuando $p$ es posición esquina, $T_x(e)(p)$ contiene de manera similar los colores de la posición que se rota hacia $p$, pero intercambiando los dos últimos de los tres colores: $T_x(e)(p)$ lleva $(a,c,b)$ donde $e(p)$ lleva $(a,c,b)$. Esto es porque todos los nombres $XY^\pm Z^\pm$, $XY^\mp Z^\mp$ de la esquina original y la esquina rotada, por convención, siempre llevan “$X$”, “$Y$”, “$Z$” en el mismo orden —el alfabético.
De esta manera tenemos una función \[ T_x\colon E \to E. \] Dado que $T_{x^3}= (T_x)^{-1}$, sabemos que $T_x$ es invertible, luego $T_x\in\mathcal{S}(E)$. Un movimiento básico es cualquiera de $T_x$, $T_y$, $T_z$, $T_{x_-}$, $T_{y_-}$, $T_{z_-}$, los últimos cinco de los cuales definiéndose de manera análoga a $T_x$.
Llamaremos una media vuelta al cuadrado \[ (x_\pm)^2, \quad (y_\pm)^2, \quad (z_\pm)^2 \] de cualquiera de los movimientos básicos (hay una media vuelta para cada cara). Generan permutaciones de orden dos. La media vuelta $x^2$ intercambia $XYZ$ con $XY^-Z$ y $XYZ^-$ con $XY^-X$; de esto se ve que $x^2$ y, de hecho, todas las medias vueltas conservan casas. El subgrupo de $G$ generado por todas las medias vueltas no sólo deja invariante $\mbox{Hab}_2$ y $\mbox{Hab}_3$, sino actúa transitivamente en ellas.
Ahora definimos el grupo de movimientos, o grupo de Rubik, como \[ G = \{ T\in \mathcal{S}(E) \ | \ T \mbox{ es una composición finita de los movimientos básicos}. \} \] Se sigue que $G$ es un grupo bajo la operación de composición, de hecho, es un subgrupo de $\mathcal{S}(E)$.
En la literatura sobre el grupo de Rubik, lo que aquí llamamos “movimientos” se acostumbra llamar “algoritmos”. Para un matemático, un algoritmo es algo diferente (de hecho, daremos uno en la segunda mitad de este artículo), lo cual nos ha motivado elegir otro vocablo aquí para denominar los elementos de $G$.
El mismo grupo $G$ actúa también en $\tilde E$. Consideremos cualquier $\tilde e\in \tilde E$, y un elemento $g\in G$. Hay un $e\in E$ (de hecho, más de uno) tal que $\pi(e)=\tilde e$. Claramente da lo mismo convertir los colores en bicolores antes o después del movimiento de los cubitos, así \[ g(\tilde e) = g(\pi(e)) = \pi(g(e)). \]
En esta acción, $G$ no es un subgrupo de $\mathcal{S}(\tilde E)$, sino que la acción tiene que entenderse en el sentido más general descrito arriba.
Aunque dijimos que no nos importa tanto el número exacto de posibles estados del cubo, nos es relevante que $\tilde E$ es mucho más pequeño que $E$, y nos queda por ver si este hecho se refleja en la dificultad relativa de su resolución.
Debido a la costumbre de leer las operaciones sucesivas de izquierda a derecha, usamos la notación convencional \[ ex=T_x(e), \] etc., de lo cual $exy = (ex)y = T_y(T_x(e))$, etc. Aunque tendemos a pensar en las combinaciones como $xy$ como permutaciones de $E$, no es exactamente la misma cosa pues, por ejemplo, $x^5$ es la misma permutación que $x$ pero es una palabra distinta en el alfabeto de las permutaciones básicas, y puede pensarse como una “operación” o “movimiento” distinto.
Como última notación especial, escribiremos $$ \enclose{circle}{X}, \enclose{circle}{Y}, \enclose{circle}{Z} $$ para indicar la rotación en $90^\circ$ del cubo entero, hacia la derecha, alrededor del eje correspondiente. El efecto es el de cambiar el significado de los movimientos que vengan escritos después de este símbolo, los cuales siempre serán relativos a la persona manejando el cubo. Por ejemplo, \[ xy \enclose{circle}{Z}^2 xy \enclose{circle}{Z}^2 \] es una forma alternativa de escribir \[ xyx_-y_- , \] para conveniencia de los que acostumbran a rotar sólo con la mano derecha.
Resumimos algunas propiedades de las permutaciones de los conjuntos finitos [5]En Wikipedia, “Grupo simétrico”.. Para cualquier conjunto $A$, dos permutaciones en $\mathcal{S}(A)$ se llaman disjuntas cuando cada elemento de $A$ es un punto fijo de una u otra de ellas. Un ciclo en $\mathcal{S}(A)$ es una permutación que deja fijo todos los elementos salvo en cierta lista $a_1,\dots,a_k$, envía $a_i$ en $a_{i+1}$ para $1\le i< k$, y envía $a_k$ en $a_1$. Cuando $k=2$, el ciclo se llama una transposición.
Demostrar la primera afirmación no es más que encontrar una solución eficiente al juego de $n$ fichas que usamos como ilustración al principio.
¿Por qué es relevante la Proposición 2? Pensemos por un momento en el conjunto $\mbox{Cub}_2\cup\mbox{Cub}_3$ de cubitos, sin pensar en sus colores. Tanto $\mbox{Cub}_2$ como $\mbox{Cub}_3$ son invariantes bajo $G$. Esto implica automáticamente que podemos considerar las acciones de $G$ en estos conjuntos por separado. Cada rotación básica define un ciclo de cuatro de las esquinas y, simultáneamente, un ciclo disjunto de cuatro de las aristas. La paridad de un ciclo $(1,2,\dots,2k)$ de un número par de elementos es impar (estoy pensando específicamente en $k=2$) y, viceversa. Por lo tanto,
Con esta poquita de preparación, y podemos sacar ya un resultado interesante:
Un estado $e$ que no está en la órbita de $e_0$ se llama comúnmente “posición imposible”.
Demostración. Supongamos que existe tal $g\in G$. Entonces $g$ se realiza como composición de rotaciones básicas. Suponiendo que $g$ intercambia dos aristas, está haciendo una permutación impar en $\mbox{Cub}_2$ y, por la Proposición 2, el número $n$ de rotaciones básicas en $g$ tiene que ser impar. Pero, por hipótesis, $g$ no mueve ninguna esquina y, por ende, hace una permutación par en $\mbox{Cub}_3$, por lo que $n$ también tiene que ser par. Esta contradicción muestra que $g$ no existe.
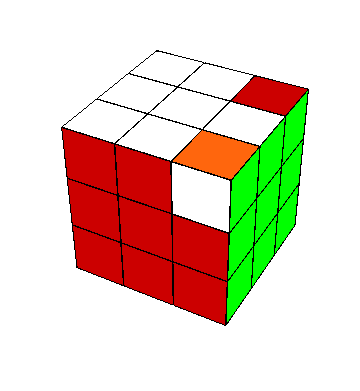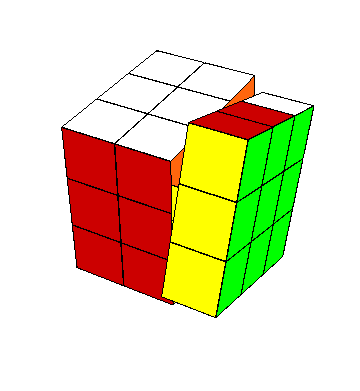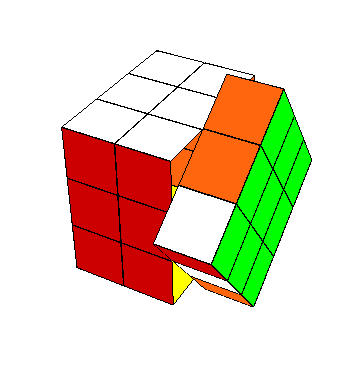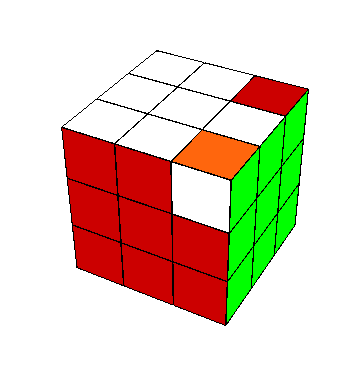 |
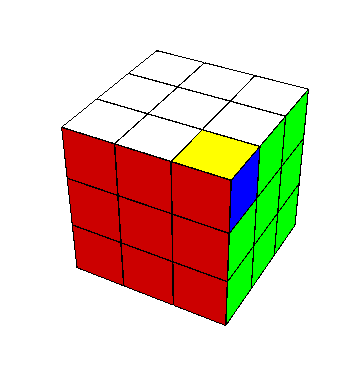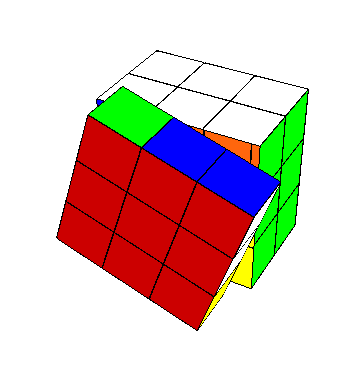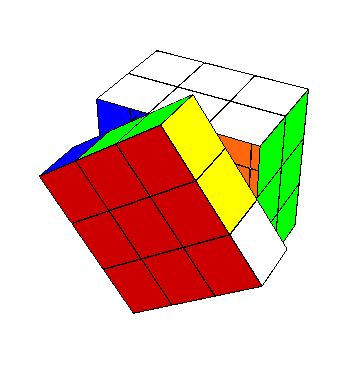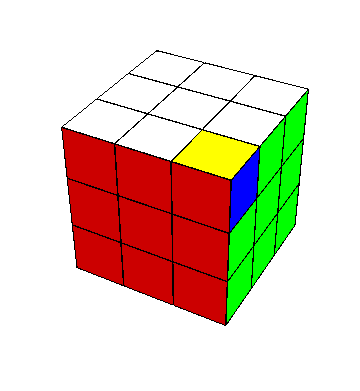 |
Con el Teorema 1, contamos con una prueba para deducir que un estado es imposible: hacemos transposiciones entre las esquinas hasta volverlas a su posición original, luego hacemos lo mismo con las aristas, contando las operaciones en cada caso. Si los dos números de transposiciones tienen paridades opuestas (o sea, si la suma es impar), entonces la posición es imposible. Queda por ver si esta prueba es determinante, o si alguna posición imposible podría pasarla.
En esta sección describimos el cubo desde la perspectiva de los bicolores, por la simple razón que esto simplifica enormemente el análisis comparado con la situación de los colores. Haremos uso de los siguiente conjuntos de estados del cubo a bicolores. \begin{eqnarray*} \tilde E_2 &=& \{ \tilde e\in\tilde E \ | \ \mbox{toda arista está en casa} \}, \\ \tilde E_3 &=& \{ \tilde e\in\tilde E \ | \ \mbox{toda esquina está en casa} \}, \\ \tilde E_2^* &=& \{ \tilde e\in\tilde E \ | \ \mbox{toda arista está alineada} \}, \\ \tilde E_3^* &=& \{ \tilde e\in\tilde E \ | \ \mbox{toda esquina está alineada} \}. \end{eqnarray*} En estas definiciones, un cubito que está en casa se dice alineado cuando todas sus caritas llevan el mismo bicolor que los centros contiguos a ellas. Desde luego $\tilde E_2^*\subseteq\tilde E_2$ y $\tilde E_3^*\subseteq\tilde E_3$, y puesto que un cubito alineado se puede considerar como ya “resuelto” en el problema a bicolores, tenemos el siguiente hecho importante.
Nos enfocamos primero en las esquinas. Recordemos que, para el estado original $\tilde e_0$, en cada casa de esquinas, los cuatro cubitos son idénticos, y las esquinas de una casa portan los bicolores en el orden cíclico opuesto a las de la otra casa. En un estado arbitrario $\tilde e$, una esquina está en casa cuando es posible rotarla en su lugar para alinear sus bicolores con todos los tres centros contiguos. ¿Cómo reconocer si está en casa o de visita? (¿Hicieron el primer ejercicio?) Una esquina que está en casa tiene $0$ o $3$ caritas con bicolor igual al de su centro contiguo. En cambio, una esquina que está de visita tiene precisamente una carita con bicolor igual al de su centro contiguo. Veamos primero las esquinas que están en casa.
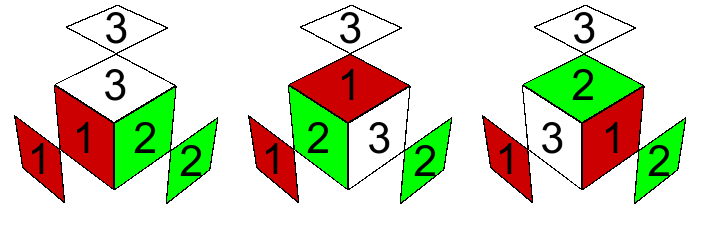
Definición. Sea $A$ una esquina en casa dentro del estado $\tilde e$. Su número de rotación $R_A$ es el el valor $R_A\in\mathbb{Z}_3$ tal que, al rotar $A$ a la derecha por un ángulo de $2\pi R_A/3$, se logran alinear sus tres caritas con los bicolores centros contiguos.
Así $R_A=0$ es lo mismo que decir que la esquina $A$ está alineada. Por eso $\tilde e\in \tilde E_3$ cuando todas las aristas en $\tilde e$ tiene número de rotación $0$.
¿Por qué pedimos que $A$ esté en casa en esta definición? Cuando está de visita, no hay manera de alinear las tres caras mediante una rotación, y tendremos que hacer algo más creativo para describir la situación. Pero, por un momento, sigamos hablando de esquinas en casa.
Definición. Sea $\tilde e\in\tilde E_3$. El número de rotación total de esquinas de $\tilde e$, $\tilde I_3(\tilde e)\in \mathbb{Z}_3 $, se define como \[ \tilde I_3(\tilde e) = \sum_{A\in\mathrm{Cub}_3} R_A \] donde esta suma se toma sobre todas las ocho esquinas $A$ del cubo.
El subconjunto $\tilde E_3$ no es invariante bajo $G$, de hecho, $\tilde ex\not\in\tilde E_3$ cuando $\tilde e\in\tilde E_3$ (un cuarto de vuelta mueve algunas esquinas fuera de su casa). Por eso pensamos en el estabilizador $G_{\tilde E_3}$ (el método de armar el cubo dependerá, en cierta etapa, de usar movimientos en $G_{\tilde E_3}$). Queremos probar que la función $\tilde I_3\colon \tilde E_3\to\mathbb{Z}_3$ es invariante bajo la acción de $G_{\tilde E_3}$. Una forma de probarlo sería la de dar una lista de generadores para $G_{\tilde E_3}$ y checar la invariancia para cada uno. Como no tengo idea de cómo encontrar los generadores, voy a extender la definición de $\tilde I_3$ a todo $\tilde E$, y usar los generadores $x_\pm$, $y_\pm$, $z_\pm$ que ya conozco para $G$.
Diremos que dos esquinas de visita $A,B$, pertenecientes a casas distintas, están alineadas entre sí cuando tienen el mismo bicolor alineado con el centro contiguo. Para este concepto, no importa la posición relativa de estas dos esquinas en el cubo.
Definición. Sean $A,B$ esquinas en el cubo a bicolores, cada una de visita en la casa de la otra. El número de rotación de $A$ relativo a $B$, $R_{AB}\in\mathbb{Z}_3$, es tal que, al rotar $A$ a la derecha por un ángulo de $2\pi R_{AB}/3$, queda alineada con $B$.
Claramente. $A$ y $B$ están alineadas entre sí precisamente cuando $R_{AB}=0$.
Las medias vueltas conservan muchas de las propiedades relacionadas con los bicolores. Aquí hay un ejemplo no trivial.
Demostración. Acabamos de observar que las medias vueltas conservan la condición de estar o no en casa. Escribamos $\tilde e(XYZ)=(\pm a, \pm b, \pm c)$, y supongamos que esta esquina está en casa, o sea, que $(\pm a, \pm b, \pm c)$ tiene el mismo orden cíclico de $(\pm1, \pm2, \pm3)$. Luego $T_x(e)(XY^-Z^-))=(\pm a, \pm b, \pm c)$, de lo cual se puede calcular que no ha cambiado el número de rotación $R_A$ de esta esquina en casa. Los demás casos de esquinas en casa son similares. Para $R_{AB}$ con dos esquinas $A,B$ de visita en casas opuestas, hay que checar las posibilidades de que ambas, una o ninguna de las dos de ellas es movida por $x$; dejamos al lector que verifique los detalles para ver que el número de rotación relativa no es alterado por $T_x$; es casi tan sencillo como la verificación para $R_A$.
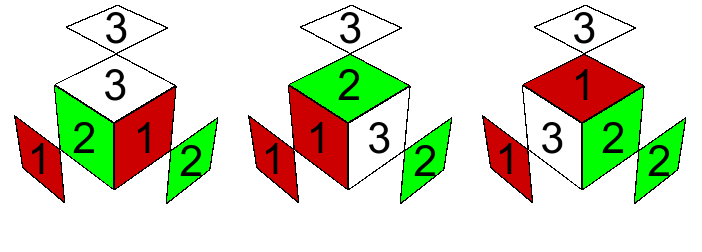
Consideremos cualquier esquina de visita. Tiene exactamente una carita alineada. Observemos que, al rotar, la esquina hacia la derecha, otra carita llega a estar alineada, y la posición de alineación (el centro de cara con que se alinea) se rota en el cubo en la dirección opuesta, hacia la izquierda.
La operación considerada en el siguiente lema no se obtiene con una rotación básica, sin embargo resultará relevante.
Demostración. Si $R_{AB}=0$, está claro que al rotar $A$, $B$ en sentido contrario, estas esquinas siguen alineadas porque los centros con que se alinean siguen órdenes cíclicos opuestos. Supongamos que $R_{AB}=1$. Digamos sin pérdida de generalidad que la carita alineada de $B$ tiene el bicolor $\pm1$. Por la transitividad de las medias vueltas dentro de las casas, podemos aplicar medias vueltas para llegar a un estado $\tilde e_1$ en que $A$ y $B$ estén en las habitaciones $XYZ$ y $XYZ^-$, o sea, en la intersección de caras $XY$ y, por el Lema 1, el número de rotación relativa no es alterado. Digamos primero que $B$ está en $XYZ$. Entonces $\tilde e_1(XYZ)=(\pm1,\pm3,\pm2)$ (el $\pm1$ es el único que tiene alineado con el centro contiguo). Dado que los bicolores en $A$ están ordenados opuestamente que en $B$ y con el supuesto de que $R_{AB}=1$ (tanto en $\tilde e$ como en $\tilde e_1$, por el Lema 1), vemos que $A$ tiene el bicolor $\pm1$ en la cara $Z^-$. Luego $\tilde e_1(XYZ^-)=(\pm3,\pm2,\pm1)$.
Rotemos $A$ a la derecha y $B$ a la izquierda para formar $\tilde e_2$ con $\tilde e_2(XYZ)=(\pm2,\pm1,\pm3)$, $\tilde e_2(XYZ^-)=(\pm1,\pm3,\pm2)$. Ahora la carita alineada de $B$ es el del bicolor $\pm3$ en la cara $Z$, y tenemos que rotar $A$ a la derecha para poner $\pm3$ en $Z$. Por definición, el número de rotación nuevamente es 1. Los otros casos se verifican de la misma manera, o más sencillamente, permutando colores en el razonamiento.
Demostración. Rotemos $B$ por $R_{AB}$ tercios de vuelta a la derecha, y llamemos $B'$ a la colocación del resultado en esta misma habitación. Comparemos $A$ con $B'$ aplicando el Lema 2: el número de rotación relativa no es alterado si rotamos ambas esquinas por $R_{AB}$ tercios de vuelta, $A$ hacia la derecha y $B'$, a la izquierda. Por definición de $R_{AB}$, estas rotaciones producen esquinas alineadas (pues $B'$ acaba como $B$) y, nuevamente, por el Lema 2, tenemos que $A$ y $B'$ también están alineadas. Esto significa que $R_{BA}$ es lo que hemos rotado $B$ a la derecha para obtener $B'$, lo cual es precisamente la definición de $R_{AB}$.
Demostración. Vamos a pensar en $B$ y $D$ como esquinas fijas, y ver lo que podemos deducir rotando $A$ y $C$. Sean $b$, $d$ los bicolores que $B$, $D$ tienen alineados. El saber cuánto rotar $A$ para que su bicolor alineado sea $d$ es cuestión de ver qué ángulo tiene su bicolor alineado actual con la cara con centro $d$, luego rotar en el sentido contrario. Lo mismo se tiene para alinear $A$ con el bicolor $b$. Por lo tanto, la diferencia $R_{AD}-R_{AB}$ es la diferencia en ángulo desde $b$ a $d$, vistos desde $A$. El mismo razonamiento dice que esta diferencia es $R_{CD}-R_{CB}$ (“visto desde $A$” es lo mismo que “visto desde $C$” por estar en la misma casa), por lo que \[ R_{AD}-R_{AB} = R_{CD}-R_{CB} .\] Aplicando el Lema 3 obtenemos la relación deseada.
El número de esquinas de una casa que están de visita en la otra casa es igual al número de esquinas de la segunda casa que están de visita en la primera. Como consecuencia de esta observación, las esquinas que están de visita siempre pueden asociarse en pares \[ (A_1,B_1), (A_2,B_2), \dots \] donde $A_j$ está de visita en la casa de $B_j$ y viceversa. Todas las formas de emparejar las esquinas de visita se obtienen simplemente reordenando $B_1,B_2,\dots$ Por el Lema 4, la suma $\sum R_{A_jB_j}$ no depende de cómo se han emparejado. Esto nos permite hacer la siguiente definición.
Definición. Sea $\tilde e\in\tilde E$. El número de rotación total $\tilde I_3(\tilde e) \in\mathbb{Z}_3$ de $\tilde e$ es la suma \[ \tilde I_3(\tilde e) = \sum R_A + \sum R_{AB} \] donde la primera suma es sobre las aristas $A$ que están en casa, y la segunda suma es sobre los pares $(A,B)$ de aristas que están de visita.
Demostración. Como siempre, basta verificar la invariancia para los movimientos básicos de $G$. Por la idea de reetiquetar los colores, basta verificar que \[ \tilde I_3(\tilde ex)=\tilde I_3(\tilde e)\] para cualquier $\tilde e\in\tilde E$. Con la aplicación de $x$, las esquinas en la cara $X$ que están en casa terminan de visita, y viceversa, mientras las esquinas restantes, que se encuentran en $X^-$, no son afectadas. En caso de que el número de esquinas en $X$ que están en casa en $\tilde e$ sea par, los emparejamos para calcular $\tilde I_3(\tilde e)$. En el caso contrario, una de ellas se emparejará con una esquina de la cara $X^-$. Entonces la afirmación es consecuencia de las siguientes dos lemas, cuyas demostraciones dejamos al lector, pues ya hemos ilustrado todos los argumentos pertinentes.
Continuamos con el estudio de los bicolores. El trato de las aristas será más fácil ya que tenemos mucha práctica con las esquinas y, además, tenemos la gran ventaja de que el número de rotación se va a poder definir, no importa en dónde esté la arista.
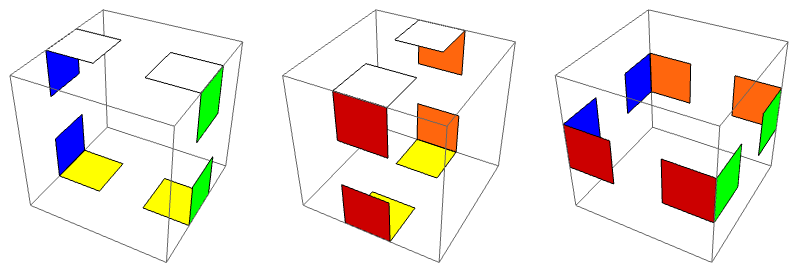
Definición. Sea $\tilde e\in\tilde E$ y sea $A$ un cubito arista en la configuración $\tilde e$. Sea $n$ (0, 1, o 2) el número de caritas de $A$ cuyos bicolores concuerdan con los centros contiguos a $A$. El número de rotación $S_A\in\mathbb{Z}_2$ es $n$ módulo 2. El número de rotación total de las aristas de $\tilde e$ es \[ \tilde I_2(\tilde e) = \sum S_A \] donde la suma es sobre las aristas $A$.
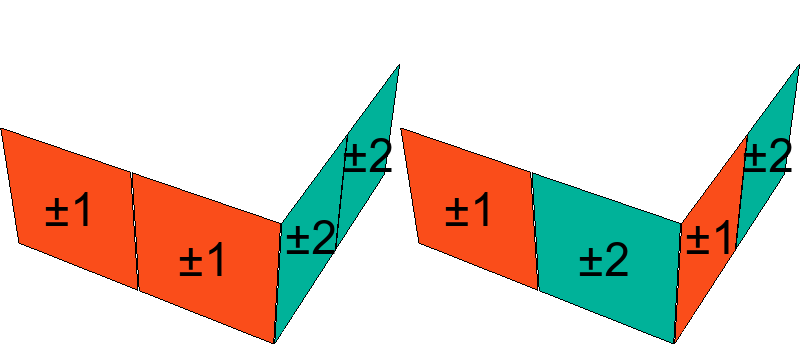 |
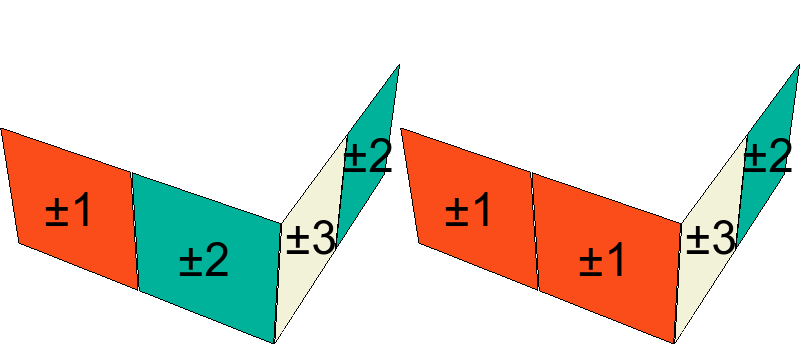 |
Demostración. Se requiere demostrarlo sólo para los movimientos básicos, y basta probarlo para $x$, rotación que no afecta a las aristas que no estén en la cara $X$. Para las cuatro que sí están, se puede ver de la figura que el número de rotación nuevo para cada arista se obtiene cambiando la paridad de su valor anterior, o sea sumando 1 (mód 2). Por lo tanto, el número de rotación total de las aristas se obtiene sumando 4 (mód 2), lo cual implica que no hay ningún cambio.
Los dos invariantes $\tilde I_2\colon\tilde E\to\mathbb{Z}_2$, $\tilde I_3\colon\tilde E\to\mathbb{Z}_3$ pueden combinarse en un solo invariante que conlleva la misma información, \[ \tilde I=(\tilde I_2, \tilde I_3)\colon \tilde E\to\mathbb{Z}_2 \times \mathbb{Z}_3 . \]
Demostración. Fijemos un cubito arista $A$ y una esquina $B$ arbitrariamente. Consideremos la siguiente operación sobre un estado $\tilde e$: rotamos $A$ y $B$ en sus lugares, por unas cantidades $S'$, $R'$. Pensemos para ilustración en $S'=0$, $R'=1$. La operación envía los estados con invariante $(S,R)=(0,0)$ en estados con invariante $(S,R)=(0,1)$ y, de hecho, es una biyección de $\tilde E$ (aunque no corresponda a un elemento de $G$). Con los otros cinco valores de $(S',R')$, obtenemos biyecciones del caso $(0,0)$ a los subconjuntos de estados con los demás invariantes.
La demostración del Teorema 4 es bastante divertida: la mayor parte consiste en mostrar explícitamente cómo resolver el problema del cubo a bicolores dado un estado $\tilde e$, bajo el supuesto de que $\tilde I(\tilde e) = (0,0)$. Esto lo daremos más adelante. ¿Por qué la solución de este problema implica que el invariante $\tilde I$ es completo? Consideremos dos estados $\tilde e_1$, $\tilde e_2\in\tilde E$ con el mismo invariante $\tilde I(\tilde e_1)=\tilde e_2$. Podemos rotar una esquina y una arista en $\tilde e_1$ como en la demostración del Lema 7 para obtener $\tilde e_1'$ con $\tilde I(\tilde e_1')=(0,0)$, y hacer lo mismo con $\tilde e_2$ para obtener $\tilde I(\tilde e_2')=(0,0)$. Entonces, por la solución práctica del problema, hay $g_1,g_2\in G$ tales que $\tilde e_1'g_1=\tilde e_0$, $\tilde e_1'g_2=\tilde e_0$. Definimos $g=g_2^{-1}\circ g_1$, luego $\tilde e_1'g=\tilde e_2'$. Claramente, da lo mismo aplicar una rotación básica a una cara antes o después de rotar un cubito en su lugar por cualquier $R'$ o $S'$. Por lo tanto, rotamos al revés la esquina y la arista en cada caso, para deducir $\tilde e_1g=\tilde e_2$. Esto muestra que, si dos estados en bicolores tienen el mismo valor de $\tilde I$, están en la misma órbita bajo la acción de $G$. Así el invariante es completo.
La composición de los invariantes con la proyección $\pi\colon E\to\tilde E$ que “confunde colores en bicolores” nos produce dos funciones de estados, \[ I_2=\pi\circ\tilde I_2\colon E\to\mathbb{Z}_2, \quad I_3=\pi\circ\tilde I_3\colon E\to\mathbb{Z}_3, \] que aparecen en los siguientes diagramas conmutativos:
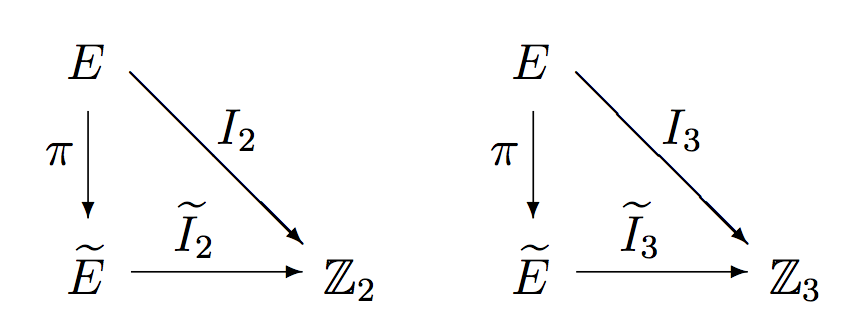
Las funciones $I_2$, $I_3$ son invariantes para la acción de $G$ en $E$ porque, como vimos, $\pi$ envía órbitas en órbitas, y cualquier función constante en órbitas en $\tilde E$ inducirá una función constante en órbitas en $E$. Sin embargo, la pareja invariante $(I_2,I_3)\colon E\to\mathbb{Z}_2\times\mathbb{Z}_3$ no es un invariante completo, como se puede ver con el ejemplo de una posición imposible: si intercambiamos dos aristas de la misma casa, colocándolas de manera que nuevamente estén alineadas, producimos un estado $e\in E$ tal que $I_3(e)=I_2(e)=0$, pero $e$ no está en la órbita de $e_0$ por el Teorema 1.
Cada $e\in E$ determina una permutación de $\mbox{Cub}_2\cup\mbox{Cub}_3$ de la siguiente manera: para cada $p\in\mbox{Hab}_2\cup\mbox{Hab}_3$, la permutación lleva al cubito referido por $e_0(p)$ al cubito referido por $e(p)$, donde $e_0$ como siempre es el estado original.
Definición. Sea $e\in E$. Se define $I_1(e)\in\mathbb{Z}_2$ como la paridad de la permutación de $\mbox{Cub}_2\cup\mbox{Cub}_3$ determinada por $e$.
En otras palabras, $I_1(e)$ es la reducción módulo 2 del número de transposiciones requeridas para mover cada esquina y arista a su posición original, sin preocuparse por los colores (o sea, sin preocuparse por rotaciones). Por la Proposición 2, $I_1$ es un invariante para la acción de $G$ en $E$. El invariante principal $I\colon E\to\mathbb{Z}_2\times\mathbb{Z}_2\times\mathbb{Z}_3$ se define por \[ I = (I_1,I_2,I_3). \]
La caracterización de los estados posibles del cubo de Rubik, basada en todo lo que hemos hecho hasta aquí, se resume en el siguiente teorema.
En particular, un estado $e\in E$ puede llevarse a la posición original $e_0$ sí y sólo si $I_1(e)$, $I_2(e)$, $I_3(e)$ son todos cero. Nuevamente, la demostración se basa en mostrar una técnica explícita para resolver el cubo desde cualquier estado para el cual el invariante $I$ es $(0,0,0)$.
Un variante sencillo del argumento de la demostración del Teorema 4 muestra que todas las órbitas de $E$ bajo $G$ tienen el mismo número de estados. Esto da el siguiente resultado.
De hecho, $\#G=\#E/12$.
Quizás sobre decir que es recomendable leer esta parte con un cubo en la mano. Supondremos que el cubo está en un estado $\tilde e$ tal que $\tilde I(\tilde e)=(0,0)$. Haremos mucho uso implícito del Lema 1.
La explicación de este primer paso es bastante larga, aunque es un procedimiento de sentido común y casi trivial. No culparé al lector que prefiera resolver esta parte por su cuenta (quizás guiado por los dibujos), en lugar de leer las instrucciones detalladas.
(i). Llenar las caritas en $Z^+$. Empezamos con un bicolor arbitrario, en esta explicación $\pm3$. Primero queremos poner todas las 8 caritas de arista con este bicolor en las caras $Z^\pm$ (desde luego, conviene escoger el bicolor que ya tiene el mayor número de caritas ya puestas.) Si alguna carita falta ponerse es porque está en una de las caras laterales $X^\pm$, $Y^\pm$. Si está, digamos, en la intersección $XY$, entonces se puede posicionar en la cara $Z$ mediante $x^{-1}$ o $y_-$, o alternativamente, se puede posicionar en $Z^-$ mediante $x_+$ o $(y_-)^{-1}$. No importa cuál de estas dos opciones escojamos, salvo que, al hacerlo, quisiéramos evitar quitar alguna carita de bicolor $\pm3$ ya metida las caras $Z^\pm$; esto puede lograrse con una o más aplicaciones previas de $z_\pm$ para “liberar el camino”. Si no hay carita $\pm3$ en ninguna intersección $X^\pm Y^\pm$ (y si todavía faltar llenar las caras $Z^\pm$ con ellas), entonces hay una en $X^\pm Z^\pm$ o $Y^\pm Z^\pm$; ésta es la situación más problemática. Supongamos sin pérdida de generalidad que hay una arista con una carita $\pm3$ en la cara $X$ y con su otra carita en $Z$ (es decir, un estado con $\pi(e)(XZ)=(\pm3,\pm b)$, donde no nos importa el valor $\pm b$.) Entonces, convierto a la situación anterior con la rotación $x_+$ (procurando primero que esto no quite algo ya puesto en $Z^-$). En todo este proceso, conviene cuidar que haya aproximadamente igual número de caritas $\pm3$ en $Z^+$ que en $Z^-$; de otro modo, cuando se llene una de estas dos caras, habrá que pasar un cubito de una a la otra para dejar espacio para poner otras nuevas; todo esto se hace fácilmente con medias vueltas $x^{\pm2}$, $y^{\pm2}$. Finalmente, se llega a la situación en que hay cuatro caritas $\pm3$ en $Z^-$ y tres, en $Z^+$. Suponiendo que el espacio en $Z^+$ junto a $Y^-$ está libre, podemos poner ahí una carita que está en $X^+$ junto a $Y^+$ mediante el movimiento \[ yz^2y^{-1}\] (puesto que las medias vueltas no afectan en esta etapa de la solución, serviría igual el movimiento $yz^2y$).
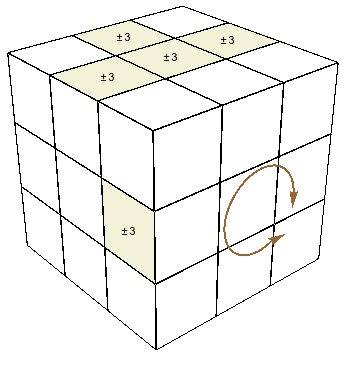
Una forma más casera de decir todo esto: ir pasando el bicolor $\pm3$ desde las caras $X^\pm$, $Y^\pm$ a las caras $Z^\pm$, siempre procurando facilitar la entrada de la siguiente carita $\pm3$ cuando sea posible.
(ii). Llenar las bandas verticales. En este momento las caras superior e inferior están “resueltas” en el sentido de que se ve una “cruz” en ellas formada del centro con cuatro aristas del mismo bicolor $\pm3$. Como primer paso en lograr la “cruz” en las caras $X^\pm$, $Y^\pm$, haremos una “banda vertical” formada del centro y las aristas que comparten carita con $Z^\pm$. Fijémonos en $X^+$, que debe llenarse con el bicolor $\pm1$. Apliquemos $z_+$ hasta que aparezca un $\pm1$ en $XZ$ (si esto no se puede, es porque todos las cuatro caritas $\pm1$ que comparten arista con $\pm3$ están contiguas con $Z^-$, situación que se rectifica con $x^2$ o $y^2$.) De la misma manera, aplicar $z_-$ hasta que aparezca un $\pm1$ debajo del centro, formando así la “banda” en $X^+$. Si hay un $\pm2$ en $YZ$, bien; y si no, aplicar $z$ hasta que lo haya—seguiremos teniendo un $\pm1$ en $XZ$ porque va saliendo de $XY$—. Hacer lo mismo con $z_-$ y tenemos la “banda” hecha en $Y$. Para fines de explicación, damos la media vuelta $\enclose{circle}{Z}^2$ al cubo en el eje $Z$; entonces, las “bandas” completadas están atrás en $X^-$, $Y^-$. Si las “bandas” no están formadas ya en $Y^+$ y $Z^+$, entonces, aplicamos $x^2$ o $y^2$, si es necesario, para acomodar un $\pm2$ en $XZ$ y un $\pm1$ en la cara $YZ^-$. Estas caritas se intercambian con el conjugado \[ z^{-1}y^2z \] sin deshacer las “cruces” y las otras “bandas” (este movimiento está en el estabilizador del complemento de las caras $X$, $Y$, visto en bicolores).
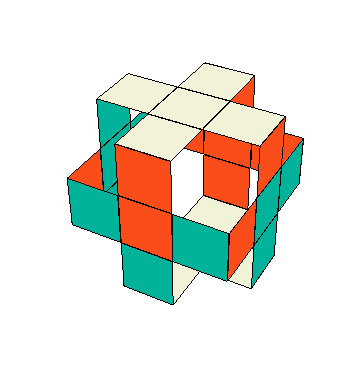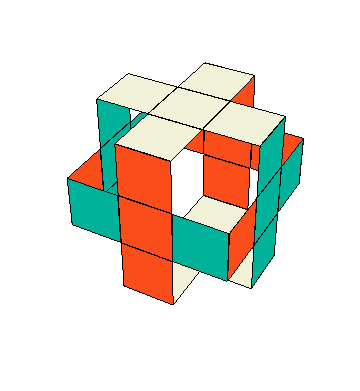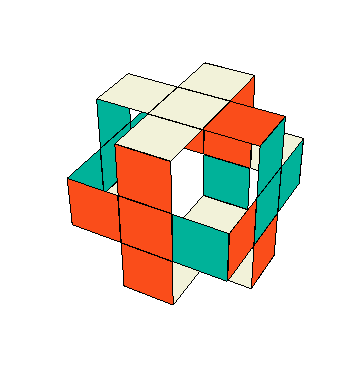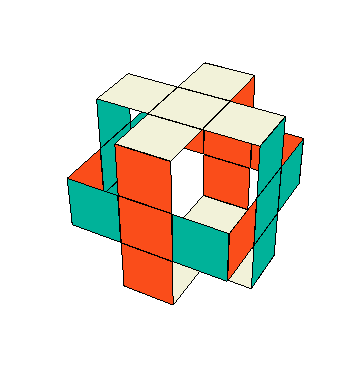
(iii). Completar las bandas horizontales. En este momento todos los cubitos arista están en casa, y los ocho que llevan el bicolor $\pm3$ están alineados; es decir, tienen número de rotación $S_A=0$. Para completar las “cruces”, tenemos que acomodar los cuatro cubitos arista en $X^\pm Y^\pm$. Puesto que $\tilde I(\tilde e)=(0,0)$ (no se habrán olvidado de la hipótesis, ¿verdad?), en particular $\tilde I_2(\tilde e)=0$, y puesto que todos los movimientos que hemos hecho no cambian el invariante $\tilde I$, sabemos que la suma de los números de rotación de los últimos cuatro cubitos arista es 0 módulo 2. Esto quiere decir que el número de ellos que no están alineados es 0, 2 o 4. Queremos que sea 0 y, suponiendo que no lo es, mediante medias vueltas ponemos dos aristas no-alineadas en la cara $X$, es decir, en $XY$, $XY^-$. Queremos “voltearlas” sin deshacer lo ya logrado. El movimiento $y^{-1}x(z_-)^{-1}$ pone uno de estos dos cubitos en $XZ$ y el otro, en $XZ^-$. Luego, la media vuelta $x^2$ los intercambia y, al aplicar la inversa de $y^{-1}x(z_-)^{-1}$, se vuelven a sus posiciones originales, pero intercambiados. Es fácil ver que el conjugado así construido \[ y^{-1}x(z_-)^{-1}\, x^2\, z_-x^{-1}y \] alinea estas dos aristas, y conserva lo que ha logrado en el sentido de los bicolores. Si todavía falta voltear un par de aristas en las bandas horizontales, entonces, las pasamos a la cara $X$ y repetimos el proceso.
En resumen, la condición $\tilde I_2(\tilde e)=0$ es suficiente para garantizar que sea posible acomodar las aristas del cubo en bicolores, es decir, para encontrar un movimiento que cambie el estado a un estado en $\tilde E_2^*$. Es obvio que también es una condición necesaria, pues si las aristas están acomodadas, entonces su número de rotación total es cero.
Después del paso 1(a), el cubo ya tiene las aristas acomodadas a bicolores, y queremos acomodar las esquinas — pero sin deshacer las aristas. En nuestra terminología, queremos llegar a un estado en $\tilde E_3^*$, mediante un movimiento que esté en el estabilizador de $\tilde E_2^*$. Recordemos (Lemas 1 y 8) que todas las medias vueltas $(x_\pm)^2$, $(y_\pm)^2$, $(z_\pm)^2$ están en este estabilizador, pero nos hará falta algo más.
El movimiento básico para acomodar las aristas es algo que me gusta llamar “reflejar un par de esquinas opuestas”. Esto significa en primera instancia, tomar un par de esquinas que se encuentran, cada una, en casa de la otra con el mismo bicolor en sus caras alineadas (o sea, con número de rotación relativa cero), intercambiarlas de casa, y alinearlas a la vez. Para hacerlo, las acomodo mediante medias vueltas (nunca olvidar las medias vueltas, gentil lector, pues no las voy a mencionar explícitamente a continuación) en la intersección de las caras $Y^-Z$, es decir, en las posiciones $XY^-Z$, $X^-Y^-Z$ o, en otras palabras, cerca de la palma de mi mano izquierda.
El movimiento, que realizo con la mano derecha, es \[ y^{-1}x^2yx^2\ z^2yz^2y = y^{-1}x^2yx^2 \ {\enclose{circle}{Y}}^{-1} \ x^2yx^2y \quad\quad {\enclose{circle}{Y}} \] el cual recuerdo más bien como “jalar, girar, empujar, girar, voltear para ver la cara de arriba, girar, empujar, girar, empujar”. El $\enclose{circle}{Y}$ al final está escrito lejos del movimiento básico, y se incluye sólo para poder hablar de la acción del grupo: este movimiento completo está en $G_{\tilde E_2^*}$, y deja invariante el conjunto de las dos esquinas mencionadas, formando una transposición en ellas.
 |
 |
 |
Este movimiento es esencialmente una composición de dos conmutadores, \[ [y^{-1},x^2] \ [z^2,y] \] seguido por $y^2$. Seguir por “$y^2$” al final tiene el efecto de transformar el $y^{-1}$ al final del conmutador en $y$, y está ahí en parte porque encuentro que es más fácil empujar con el dedo gordo de la mano derecha que jalar con toda la mano, pero también porque este movimiento tendrá un uso importante más adelante.
Las dos esquinas así reflejadas terminan en las posiciones $XY^-Z$ y $XY^-Z^-$, por si uno quiere observar qué es lo que pasó con ellas. Lo importante del movimiento de reflejar un par de esquinas opuestas es que estabiliza $\tilde E_2^*$, a la vez que revuelve las demás esquinas sin afectar sus números de rotación. Estas afirmaciones son fáciles de verificar simplemente observando a dónde va a dar cada cubito.
Este movimiento no sirve solamente para reflejar esquinas alineadas: se puede aplicar a otras situaciones. Todo el mundo sabe que, cuando reflejamos una esquina dos veces con respecto al mismo bicolor, regresa a cómo estaba. Pero cuando se refleja con respecto a caritas distintos, el resultado es una rotación de la esquina: una rotación puede descomponerse como composición de dos reflexiones. Entonces, si se aplica la operación llamada “reflejar un par de esquinas opuestas” a un par de esquinas rotadas (cuando estoy trabajando el cubo tiendo a decirme “rotada” como sinónimo de “en casa, pero no alineada”), terminarán reflejadas (que es sinónimo para “de visita”). Quizás no resulten alineadas entre sí, pero ahora se podrán emparejar con otras esquinas para continuar el proceso.
En otras palabras, la estrategia para alinear todas las esquinas es de ir reduciendo el número total de esquinas rotadas y de esquinas reflejadas, llegando finalmente a que todas estén en casa y alineadas. Encuentro que es buena idea emparejar una rotada con una reflejada: después de la operación tendré una reflejada y una ya alineada. Luego la que está reflejada puede emparejarse con alguna otra rotada, si es que hay.
Es posible que, por mala suerte (o falta de previsión), se llegue a tener dos esquinas reflejadas, pero están en la misma casa (podemos decir “a contraesquina”) y así no es posible juntarlas mediante medias vueltas para “reflejar un par de esquinas opuestas”. Entonces, hay que “echarse para atrás” con alguna reflexión que alinee una de estas equinas y desalinee otra que estaba alineada. A este proceso de introducir una tercera esquina en el proceso le llamo “triangulación”. Similarmente, si hay sólo dos esquinas $A$ y $B$ rotadas y en la misma casa, también hay que echarse p'atrás y triangular.
Finalmente llegamos a que hay sólo dos esquinas no acomodadas, y estas dos están reflejadas y pertenecen a casas opuestas. Ahora aplicamos la hipótesis de que el estado original tenía invariante $I_3(\tilde e)=0$. Esto quiere decir que el número de rotación relativa de estas dos esquinas es cero (pues las demás no contribuyen nada al número de rotación total). En otras palabras, estas dos últimas esquinas están alineadas entre sí, y podemos acomodarlas con una reflexión más.
La conclusión es que, conociendo un solo movimiento para “reflejar un par de esquinas opuestas”, auxiliado por medias vueltas, y partiendo de un estado en $\tilde E_2^*$ para el cual $I_3=0$, es posible acomodar las esquinas a bicolores, llegando a un estado en $\tilde E_2^*\cap\tilde E_3^*$. Por la Proposición 4, el cubo queda resuelto a bicolores.
Uno puede agregar más movimientos a su repertorio, para hacer el procedimiento más eficiente. Por ejemplo, el movimiento impar \[ (y^{-1}x^2)^4 \ y \] (“jalar, voltear, \dots”) refleja simultáneamente dos pares de esquinas: las de la intersección $XY^-$ y las de $YZ^-$. Un movimiento par que refleja cuatro esquinas es \[ y\ (x^2{\enclose{circle}{Y}})^4 \; y_- . \]
Hasta aquí podemos atrevernos a decir que el cubo a bicolores es, efectivamente, más fácil de resolver que el cubo a colores. Hemos dividido el problema en una serie de partes más sencillas.
Puesto que ahora nos interesan los colores, debemos pensar en subconjuntos de $E$, a saber: \begin{eqnarray*} E_2 &=& \{ e \ | \ \mbox{toda arista está en casa} \}, \\ E_3 &=& \{ e \ | \ \mbox{toda esquina está en casa} \}, \\ E_2^* &=& \{ e \ | \ \mbox{toda arista está alineada} \}, \\ E_3^* &=& \{ e \ | \ \mbox{toda esquina está alineada} \}. \end{eqnarray*} Los dos primeros se podrían definir como $E_2=\pi^{-1}(\tilde E_2$) y $E_3=\pi^{-1}(\tilde E_3)$. En la práctica, con un verdadero cubo, sólo estábamos imaginándonos que era un cubo de bicolores: con los pasos 1(a) y 1(b) realmente llegamos a un estado $e\in E$ con $\pi(e)\in \tilde E_2^*\cap\tilde E_3^*$. El reto ahora es pasar de $\tilde E_2^*$ a $\tilde E_2$ y de $\tilde E_3^*$ a $\tilde E_3$.
Partimos de un estado $e$ del cubo en $\pi^{-1}(\tilde E_2^*\cap\tilde E_3^*)$, es decir, resuelto a bicolores. Esto implica que $I_2(e)$ e $I_3(e)$ se anulan. Para resolverlo a colores, conviene trabajar primero las esquinas. Por lo menos, así lo creo yo, porque el plan es de llegar a $E_3^*$ con movimientos que estén en la intersección de estabilizadores $G_{\tilde E_2^*}\cap G_{\tilde E_3^*}$; luego, en el siguiente paso, tendremos que llegar a $E_2^*$ mediante $G_{\tilde E_2^*}\cap G_{E_3^*}$ (efectivamente, ¡hablamos simultáneamente de las acciones de $G$ sobre conjuntos diferentes!). Me parece que sería mucho más difícil llegar de $E_2^*$ a $E_3^*$ con $G_{ E_2^*}\cap G_{\tilde E_3^*}$. Afortunadamente, todavía podemos usar las medias vueltas libremente, pues ellas están en $G_{\tilde E_2^*\cap\tilde E_3^*}$.
Para ello, nos fijamos en cualquier habitación esquina, digamos en la posición $XY^-Z$ cerca del pulgar izquierdo. Puesto que $e\in E_2\cap E_3$, la esquina $(1,-2,3)$ que debería ir en esta posición ya está en casa. Es fácil acomodarla en su habitación con una o dos medias vueltas (si está en $Z^-$, con una media vuelta se sube a $Z$, luego si esto no la pone en $XY^-Z$ tiene que estar en $X^-YZ$, y otra media vuelta la pone en $XY^-Z$). De la misma manera, con medias vueltas que no mueven $XY^-Z$ (o sea con $(x_-)^2$, $y^2$, $(z_-)^2$) ponemos la esquina $(-1,-2,3)$ en $X^-Y^-Z$, y luego, con $y^2$, $(z_-)^2$, ponemos $(-1,2,3)$ en $X^-YZ$. La única media vuelta que no mueve estas tres esquinas ya acomodadas es $(z_-)^2$, y si $(1,2,3)$ no está ya en $XYZ$, no hay manera de acomodarla con medias vueltas: necesitamos un movimiento más complicado.
Si ahora todas las esquinas están acomodadas, este paso ha terminado. Sin embargo, esto es poco probable. Aun si todas las esquinas de la cara $Z$ están en su lugar, es posible que algunas de la cara $Z^-$ estén fuera de lugar. En tal caso, rotamos todo el cubo (cambiando el significado de $1$, $2$, $3$ también para fines de explicación) con tal de volver a la situación descrita en el párrafo anterior: en la cara $Z^+$, las esquinas bien acomodadas dibujan una forma de “L invertida” o “7 de cabeza”. La cuarta esquina $(1,2,3)$ tiene que estar en una de las habitaciones de su propia casa en la cara $Z^-$, luego, por una media vuelta (si es necesaria), la ponemos en $XY^-Z^-$, o sea, debajo de $(1,-2,3)$. Con cuatro esquinas así, vemos que no quedan muchas combinaciones a considerarse para las cuatro esquinas restantes.
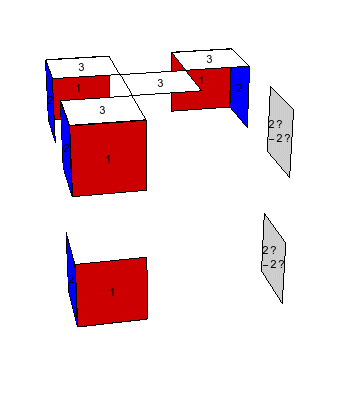 |
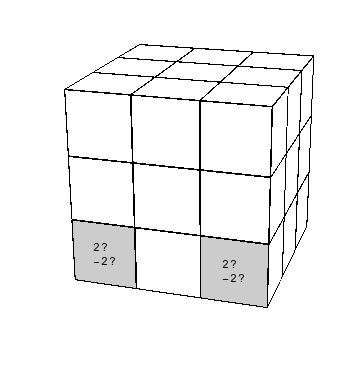 |
Dejemos un momento la descripción del algoritmo para volver a la teoría. De la misma forma que el Lema 1 describe las esquinas, tenemos para las aristas lo siguiente (que a estas alturas debe ser bastante obvio).
Las esquinas $(1,-2,3)$ y $(-1,2,3)$ son de la misma casa, que llamaremos la casa impar de esquinas por tener un número impar de signos “$-$“ en la notación. Las otras dos esquinas de esta casa son $(1,2,-3)$ y $(-1,-2,-3)$, las cuales, o bien están también bien acomodadas, o bien están intercambiadas. En la otra casa, la casa par, tenemos $(-1,-2,3)$ bien acomodada y $(1,2,3)$ fuera de lugar en $XY^-Z^-$. Esto implica que las dos restantes, a saber $(1,-2,-3)$ y $(-1,2,-3)$, ocupan los lugares $XYZ$ y $X^-YZ^-$. Para ellas, también hay dos posibilidades: que estén en el orden mencionado; o bien, al revés.
Por lo anterior, quedan cuatro combinaciones a tratar pero, afortunadamente, las podemos reducir a dos. Para no entrar en explicaciones muy largas, consideremos primero qué pasa cuando $(1,-2,-3)$ está en $XYZ$ y $(-1,2,-3)$ está en $X^-YZ^-$. Entonces $(-1,2,-3)$ está bien acomodado, mientras las dos esquinas \[ (1,2,3),(1,-2,-3) \] están cada una en la habitación que pertenece la otra. Esto significa que hay una permutación impar en la casa par para este caso. Si en la casa par, las esquinas $(1,2,-3)$ y $(-1,-2,-3)$ también están intercambiadas, entonces hay una permutación par en $\mbox{Cub}_3$ (recordemos la descomposición de cualquier permutación en ciclos disjuntos de la Proposición 1, y la caracterización de la paridad de la Proposición 2). Por otra parte, en el segundo caso, cuando $(1,-2,-3)$ está en $X^-YZ^-$ y $(-1,2,-3)$ está en $XYZ$, las tres esquinas \[ (1,2,3), \ (1,-2,-3), \ (-1,2,-3) \] están desplazadas cada una al lugar perteneciente a la que le sigue en orden cíclico formando un ciclo de orden tres, que es una permutación par. La combinación con la posible transposición de las dos esquinas de la casa impar ahora produce la paridad opuesta para la permutación de $\mbox{Cub}_3$ en comparación con el primer caso.
Esto sugiere tratar sólo dos situaciones: paridad par o impar de la permutación de $\mbox{Hab}_3$. ¿Cómo detectarla rápidamente? La regla es la siguiente: examinemos las caritas en $XYZ$, $XYZ^-$ visibles en la cara $Y$. Estas caritas serán las señaladoras de paridad. Puesto que el cubo ya está resuelta a bicolores, estas caritas lleven los colores $+2$ o $-2$.
Esto puede verificarse simplemente identificando la señaladoras de paridad para los cuatro casos.
En ambos casos, rotemos el cubo con ${\enclose{circle}{Y}}^{-1}{\enclose{circle}{Z}}$ para poner las señaladoras de paridad enfrente de nosotros en la intersección $XZ^-$.
Caso impar de las esquinas. Para el caso impar, hacemos \[ (y^{-1}x^2)^4y\ z_- \ [x,y]^3 \ (z_-)^{-1} . \]
Parece largo, pero ¿se acuerdan del “movimiento impar” que se aplicaba en el problema de las esquinas a bicolores? Esta primera parte deja reflejadas las cuatro esquinas que deja en la cara $X$. La segunda parte contiene una potencia del conmutador $[x,y]^3=(xyx^{-1}y^{-1})(xyx^{-1}y^{-1})(xyx^{-1}y^{-1})$ (“aprieta, jala, afloja, empuja, ... ”), que refleja las esquinas en la intersección $XZ$ y en $YZ^-$. Por eso conjugamos por $z_-$, para que el conmutador refleje las esquinas que fueron movidas por la primera parte (en la literatura sobre el cubo de Rubik este tipo de combinación se conoce como “preparar” el movimiento con $z_-$; luego me supongo que hay que “despreparar” con la inversa.)
Después de este movimiento (que es impar porque la primera parte es impar y los conmutadores siempre son pares), es muy fácil acomodar todas las ocho esquinas con medias vueltas. La demostración, nuevamente tediosa, se puede hacer siguiendo las esquinas en los dos subcasos del caso impar.
Caso par de las esquinas. Para el caso par, no tenemos que aprender ningún movimiento nuevo. Simplemente hacemos el movimiento de “reflejar un par de esquinas opuestas”. Esto produce un par de esquinas reflejadas en la intersección $XY^-$. Para rectificar esto, simplemente actuamos como si estuviéramos otra vez en el paso 1(b). Explícitamente, primero movemos el cubo con ${\enclose{circle}{Y}}$ y volvemos a reflejar el par de esquinas opuestas. Igual que en el caso impar, ahora se terminan de acomodar las esquinas con medias vueltas; la verificación se da por el mismo razonamiento.
Un aspecto interesante de este paso es que la condición $I_2(e)=0$, $I_3(e)=0$ es suficiente para resolver las esquinas a colores y las aristas a bicolores: no hacía falta ningún invariante adicional para este paso.
No me sorprendería que alguien encontrara unos movimientos mucho más cortos para lograr la solución de las esquinas a colores.
Ahora cerramos con broche de oro. Tenemos un estado $e\in E_3^*$ tal que $\pi(e)\in\tilde E_2^*$. Las esquinas están bien acomodadas: en sus habitaciones y alineadas, a la vez que todas las aristas están en su casa, y alineadas en el sentido de bicolores. Sólo falta poner cada arista en su propia habitación sin perder las condiciones ya obtenidas: necesitamos movimientos en $G_{\tilde E_2^*}\cap G_{E_3^*}$.
Observemos que el movimiento \[ (x^2y^2)^3 \] intercambia las aristas en $XZ$, $XZ^-$, y también intercambia $YZ$ con $YZ^-$. Acostumbro decir que “voltea columnas contiguas”.
Por lo mismo, el movimiento compuesto $$ (x^2y^2)^3 \ \enclose{circle}{Z}\ (x^2y^2)^3 \ {\enclose{circle}{Z}}^{-1} $$ intercambia $XZ$ con $XZ^-$ y $X^-Z$ con $X^-Z^-$ (“voltea columnas opuestas”); el ${\enclose{circle}{Z}}^{-1}$ al final está sólo para facilitar esta descripción. Se obtiene el mismo resultado más rápidamente con $$ x^2 \ y^2y_-^2 \ \ (x_-)^2 \ y^2y_-^2 = x^2 \ y^2{\enclose{circle}{Y}}^2 y_-^2 \ x^2 \ y^2{\enclose{circle}{Y}}^2y_-^2.$$ Aplicando diversas otras conjugaciones a $(x^2y^2)^3$, podemos intercambiar pares de aristas aunque no estén opuestas; uno de los casos más difíciles, intercambiar simultáneamente $XY$ con $XY^-$ y $XZ$ con $XZ^-$, se logra con $$ z^{-1}z_-\ x \ (x^2y^2)^3 \ x^{-1} (z_-)^{-1} z. $$ Siempre es la misma idea: acomodo los pares a intercambiarse en la posición de columnas contiguas u opuestas.
Así, cuando el número de aristas fuera de sus habitaciones es cuatro o más, podemos reducir este número por dos. Cuando el número de aristas fuera de su habitación es igual a tres, se puede acomodar todas las tres por medio del movimiento $$z^2 \ y^{-1}y_- \ x^2 \ y(y_-)^{-1} = z^2 \ y^{-1}{\enclose{circle}{Y}}y_- \ z^2 \ y \enclose{circle}{Y}(y_-)^{-1}, $$ posiblemente con unas medias vueltas primero.
Este movimiento produce un ciclo de orden tres, con las posiciones $XZ$, $XZ^-$, $X^-Z^-$. Es físicamente imposible que el número de aristas fuera de su habitación sea uno (porque otra tendría que ocupar su lugar). Tampoco el número puede ser dos, pues una transposición de únicamente dos aristas significaría $I_0(e)=1$ (mód 2), contrario a la hipótesis de que $I(e)=(0,0,0)$ en el Teorema 5. Por lo mismo, el Teorema 5 queda demostrado.
Si todo lo anterior le pareció complicado, una de las razones podría ser que mucha justificación teórica venía intercalada dentro de la exposición del algoritmo de solución. Como sea, en plan de recompensa para el lector diligente que ha llegado a este punto, ofrecemos una demostración por video que esperamos no vaya a complicar las cosas más.
[1] J.Chen, “Group theory and the Rubik's cube”, descargado de http://www.math.harvard.edu/~jjchen/ 25 marzo 2016.
[2] Porter, R. Michael, “Invariantes algebraicos y el cubo de Rubik”. Conferencias Generales, IV Coloquio de Matemáticas del Departamento de Matemáticas del Cinvestav (Taxco, Guerrero, 1985) (1987) p. 91—130.
[3] En Wikipedia, “Acción (matemática)”, descargado 25 marzo 2016.
[4] En Wikipedia, “Grupo (matemática)”, descargado 25 marzo 2016.
[5] En Wikipedia, “Grupo simétrico”, descargado 25 marzo 2016.

Nació en Los Ángeles, EEUU en 1952. Después de cursar la licenciatura en matemáticas en Harvard College en 1973, completó la maestría y el doctorado en Northwestern University. Al terminar, en 1978, ingresó al Departamento de Matemáticas del Centro de Investigación y Estudios Avanzados (CINVESTAV-IPN), en el que ha permanecido hasta el presente. En 2006, fundó la sede de este departamento en la Unidad Querétaro del CINVESTAV, donde se encuentra actualmente.
Su tesis doctoral y primeros trabajos se centraron en el área de los espacios de Teichmüller y los grupos kleinanos, tema que tiene su fundamento en el fenómeno de la transformación conforme, mismo que ha sido de alguna manera el motif de la mayoría de sus trabajos posteriores; ya sea en funciones univalentes de una variable compleja o en cómputo numérico de transformaciones conformes y casiconformes, en el estudio de las transformaciones de Möbius en cuaternios o en el análisis hiperholomorfo. Otros de sus intereses matemáticos incluyen las ecuaciones diferenciales y la matemática financiera. Ocasionalmente, ha colaborado con investigaciones en otras disciplinas, como la biología celular y la biotecnología. Es miembro del Sistema Nacional de Investigadores desde 1985, nivel III.
Su tiempo "libre" se reparte entre la música, el t'ai chi, el estudio de idiomas (es esperantista activo) y esfuerzos por la unidad del género humano como miembro de la fe Bahá'í.
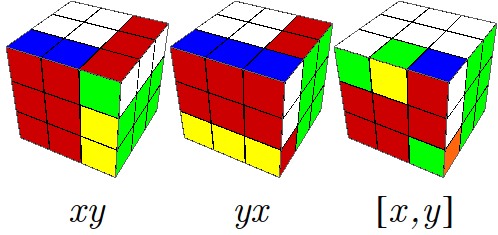
![$[x,y]^6=\mathbf{1}$](rubikfiguras/figcommpowers.gif)