

El modelo matemático de una red es un grafo (o gráfica) cuyos nodos o vértices son las terminales y sus aristas son las interconexiones. Una de las cuestiones a tener en cuenta en el diseño de una red es la siguiente: Ante la posibilidad de fallas en las conexiones, ¿ cuál es la probabilidad de que las terminales sigan interconectadas? Esta cuestión es central para el diseñador que siguiendo un presupuesto limitado debe diseñar una nueva interconexión que optimize la probabilidad de interconectividad. En esta nota nos restringimos al caso de grafos desorientados, es decir, flujo de datos bidireccionales en las interconexiones y terminales perfectas, solo las interconexiones pueden fallar.
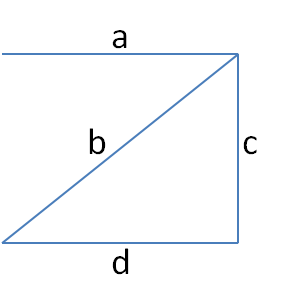
El modelo matemático de una red con nodos perfectos y posibilidad de fallas en sus aristas es un grafo tal que cada arista $e$ tiene asociada un parámetro de Bernoulli $p_{e}$ que se interpreta como su probabilidad de operación tal que estos parámetros están independientemente distribuidos. Esto es un grafo estocástico. Los estados del grafo es el conjunto de partes de sus aristas. Cada estado $\mathcal{E}\in \mathcal{P}\big(E(G)\big)$ determina un subgrafo $G_{\mathcal{E}}< G$ cuyos vértices coinciden con los de $G$ y el conjunto de sus aristas es el estado $\mathcal{E}$. Decimos que un estado $\mathcal{E}$ es operativo si el subgrafo $G_{\mathcal{E}}$ es conexo. Definimos la confiabilidad $R(G)$ del grafo $G$ como la probabilidad de que un estado sea operativo: $$R(G)= P(\mathcal{E}\ es\ operativo)$$ Concretamente, debido a que los parámetros de Bernoulli están independientemente distribuidos, tenemos la siguiente expresión: \begin{equation}\label{cuenta1} R(G)=\sum_{\mathcal{E}\ es\ operativo }\ \prod_{e\in \mathcal{E}}\ p_{e}^{\chi_{\mathcal{E}}(e)}(1-p_{e})^{1-\chi_{\mathcal{E}}(e)} \end{equation} donde $\chi_{\mathcal{E}}$ es la función indicadora de $\mathcal{E}$: es uno si $e\in\mathcal{E}$ y cero en otro caso. A modo de ejemplo, considere el grafo $G$ de la Figura 1. Sus estados operativos son: $\{a,b,d\}$, $\{a,c,d\}$, $\{a,b,c\}$ y $\{a,b,c,d\}$. Así tenemos la confiabilidad de $G$: $$R(G)= p_{a}p_{b}(1-p_{c})p_{d} + p_{a}(1-p_{b})p_{c}p_{d}+p_{a}p_{b}p_{c}(1-p_{d})+p_{a}p_{b}p_{c}p_{d}$$
Como algoritmo de cálculo, el anterior procedimiento es ineficiente ya que debemos buscar la lista de estados operativos para utilizar la expresión \eqref{cuenta1}. El siguiente teorema de factorización simple [4]F. Moskovitz y R.A.D. Center, The analysis of redundancy networks, Rome Air Development Center, Air Research and Development Center, United States Air Force, 1958. soluciona este problema:
La factorización anterior de un algoritmo recursivo para el cálculo exacto de la confiabilidad. La recursión termina en el caso de un grafo sin aristas donde la confiabilidad es:
$$R(n\ nodos) = \left\{ \begin{array}{c l} 1 & \ \ \ n=1\\ 0 & \ \ \ n>1 \end{array} \right.$$El anterior es el algoritmo Fact [3]C.J. Colbourn, The Combinatorics of Network Reliability, New York, Oxford University Press, 1987., [6]A.Satyanarayana, M.Chang, Network Reliability and the Factoring Theorem, Networks, 13 (1983), 107-120.. Podemos mejorarlo de la siguiente manera. El conjunto de estados operativos es coherente: si $\mathcal{E}$ es operativo y $\mathcal{E}\subset\mathcal{F}$ entonces $\mathcal{F}$ es operativo. En particular, la inclusión define un orden parcial en el conjunto de estados operativos y respecto de este tenemos los estados operativos minimales.

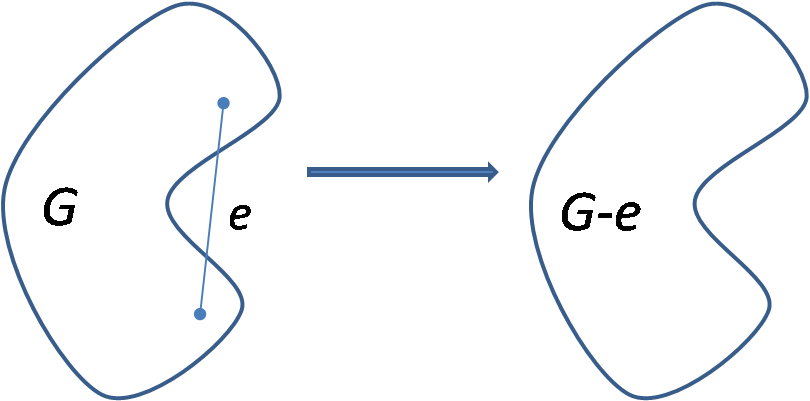
Decimos que un arista $e$ es irrelevante si no pertenece a ningún estado operativo minimal. Por ejemplo, toda arista cuyos vértices finales son coincidentes es irrelevante.
De esta manera, quitando en cada iteración del algoritmo recursivo Fact las aristas irrelevantes, tenemos un algoritmo más eficiente.
A todo grafo $G$ podemos asignar variables de Bernoulli idéntica e independientemente distribuidas con parámetro $p$. A este nuevo grafo estocástico lo denotamos por $(G,p)$. Definimos el polinomio de confiabilidad como: $$R_{G}(p)= R\big((G,p)\big)$$ Este es un invariante del grafo $G$. Entre sus propiedades tenemos que este polinomio tiene grado igual número de aristas de $G$ y que el coeficiente del término de menor grado es el número de árboles generadores de $G$ cuyo número de aristas coincide con el grado respectivo: $$R_{G}(p)= S(G)p^{g}+\ldots C_{n}p^{n}$$ tal que $n$ es el número de aristas de $G$. Como consecuencia, debido a que la complejidad computacional del número de árboles generadores es $NP$-completo, la complejidad del polinomio de confiabilidad es al menos $NP$-completo.
A modo de ejemplo, considere el grafo $G$ de la Figura 1. Sus árboles generadores son: $\{a,b,d\}$, $\{a,c,d\}$ y $\{a,b,c\}$. Su polinomio de confiablidad es: $$R_{G}(p)= 3p^{3}-2p^{4}$$
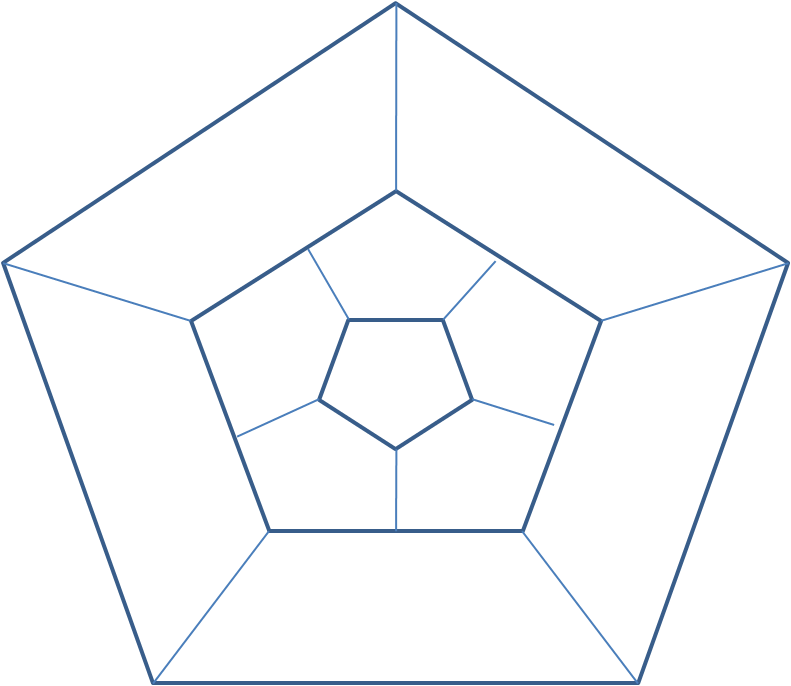
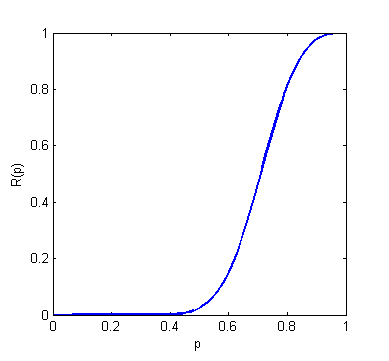
Como ejemplo menos trivial, considere el dodecaedro $D$ de la Figura 4. Su polinomio de confiabilidad es: \begin{multline}\label{cuenta2} R_{D}(p)= -1111968 \ p^{30} + 13883040 \ p^{29} -78957900 \ p^{28} + 270058080 \ p^{27}\\ -617291520 \ p^{26} + 990271044 \ p^{25} -1137887555 \ p^{24} + 936723060 \ p^{23}\\ -541514640 \ p^{22} + 209417160 \ p^{21} -48772800 \ p^{20} + 5184000 \ p^{19} \end{multline} Su gráfica se ilustra en la Figura 5. ¿ Puede el lector describir explícitamente los $5184000$ árboles generadores del dodecaedro?
En la práctica, la confiabilidad de las aristas, los parámetros de Bernoulli, son muy cercanos a uno. De esta manera, el comportamiento asintótico de la confiabilidad para parámetros de Bernoulli cercanos a uno es una muy buena aproximación de la misma.
Definimos $N_{m}$ como el número de estados no operativos con $n-m$ aristas siendo $n$ el número de aristas de $G$. Decimos que el grafo $G$ es $m$-conexo si $m$ es el natural más pequeño tal que $N_{m}$ es distinto de cero. El siguiente Teorema es la versión matemática de la conocida frase:
Como corolario tenemos la fórmula de Burtin-Pittel [7]Yu.D. Burtin, B.G. Pittel, Asymptotic estimates of the reliability of a complex system, Engineering Cybernetics, 10 (1972), 445-451.:
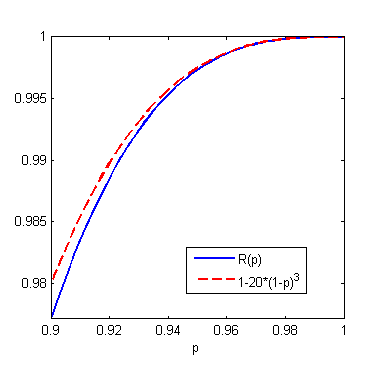
A modo de ejemplo considere el dodecaedro $D$ de la Figura 4. El dodecaedro es $3$-conexo y su conjunto los estados no operativos con $n-3$ aristas ($n=30$ es el número de aristas del dodecaedro) son $$E(D)-\{e\in E(D)\ /\ e\ es\ adyacente\ a\ v\}$$ para todo vértice $v\in V(D)$. En particular $N_{3}= |V(D)|= 20$ y por la fórmula de Burtin-Pittel tenemos: $$R_{D}(p)=1- 20(1-p)^{3}+O\big((1-p)^{4}\big)$$ Compare la fórmula anterior con la expresión \eqref{cuenta2} (ver Figura 6).
Debido a que la complejidad computacional del cálculo de la confiabilidad es del tipo NP-completo (de hecho NP-hard), cabe la pregunta acerca de cómo hacer procesamiento paralelo. Nos gustaría intercambiar tiempo de cálculo por espacio de cálculo. Es decir, supongamos que tenemos a nuestra disposición múltiples computadoras y queremos, en pós de ahorrar tiempo de cálculo, dividir el problema, procesar cada parte independientemente y con esos resultados calcular la confiabilidad total. Para esto precisamos un Teorema de factorización de la confiabilidad. Es interesante observar que aunque contemos con todas las súpercomputadoras que queramos, si no contamos con un Teorema de factorización apropiado que nos indique cómo separar el problema, no podremos hacer procesamiento paralelo. Es decir, no importa qué tecnoloía contemos, el procesamiento paralelo es un problema matemático.
Concretamente, solucionamos el siguiente problema: Dado un grafo estocástico $G$ y subgrafos $G_{1}$ y $G_{2}$ tales que su unión es $G$ y su intersección son $n$ vértices, expresar la confiabilidad de $G$ mediante una fórmula que contenga las confiabilidades de los grafos $G_{1}$, $G_{2}$ y todas las posibles identificaciones en los vértices compartidos.
Como ejemplo, considere un grafo $G$ con la propiedad de que puede ser descompuesto en subgrafos $G_{1}$ y $G_{2}$ compartiendo los vértices $a$ y $b$ solamente. Denotando por $\hat{G}_{i}$ el grafo resultante de identificar los vértices compartidos $a$ y $b$ en el grafo $G_{i}$, tenemos la fórmula de factorización: $$R(G)=R(\hat{G}_{1})R(G_{2})+ R(G_{1})R(\hat{G}_{2}) - R(G_{1})R(G_{2})$$ Esta fórmula se ilustra en la Figura 7.

Etiquetemos los $n$ vértices compartidos con los naturales $\{1,2,\ldots n\}$ y considere la particiones $Part_{n}$ de este conjunto. Para cada partición $\mathcal{A}\in Part_{n}$ denotamos por $G_{i}^{\mathcal{A}}$ al grafo resultante de identificar los vértices compartidos de $G_{i}$ de acuerdo a las clases de la partición $\mathcal{A}$. Definimos el producto $\mathcal{A}\cdot\mathcal{B}$ de dos particiones $\mathcal{A}$ y $\mathcal{B}$ como la partición más fina que es más gruesa o igual que $\mathcal{A}$ y más gruesa o igual que $\mathcal{B}$. Con este producto, el conjunto de particiones $Part_{n}$ es un monoide (o semigrupo) conmutativo cuya unidad es la partición $\big\lbrace \{1\}, \{2\}, \ldots \{n\} \big\rbrace$. Definimos la partición trivial como $\big\lbrace \{1,2,\ldots n\}\rbrace$.
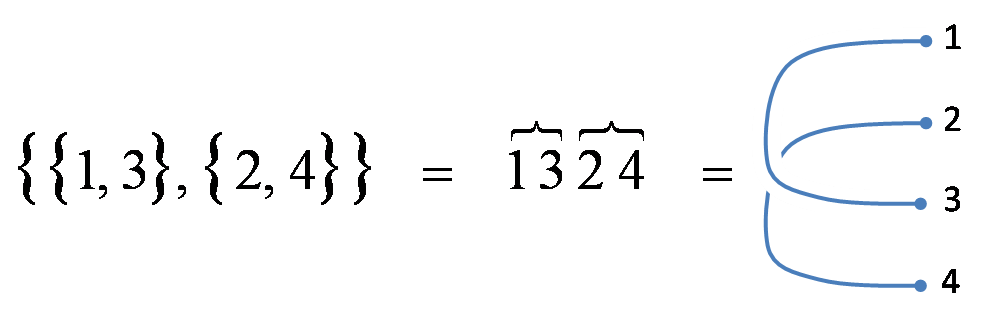
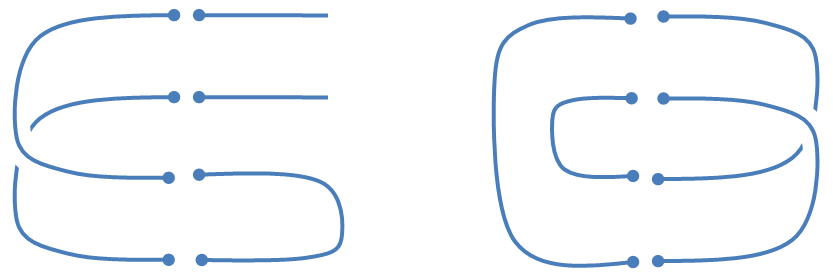
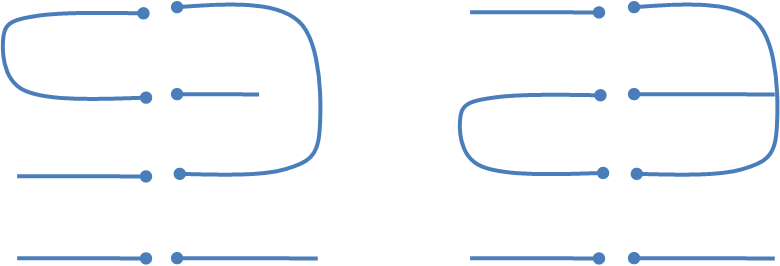
La Figura 8 muestra un ejemplo de cómo denotar y diagramar una partición y las Figuras 9 y 10 muestran productos de particiones triviales y no triviales respectivamente. Queda claro en estas Figuras la relación entre la trivialidad del producto y la conexidad del diagrama resultante. Definimos la matriz de conexidad $A_{n}=\big(a_{\mathcal{A}\mathcal{B}}\big)$ tal que $a_{\mathcal{A}\mathcal{B}}=1$ si $\mathcal{A}\cdot\mathcal{B}$ es trivial y $a_{\mathcal{A}\mathcal{B}}=0$ en otro caso. La siguiente es la fórmula del determinante [2]J.M.Burgos, Factorization of network reliability with perfect nodes II: Connectivity matrix, Discrete Applied Mathematics, Volume 198, 2016.: $$det(A_{n})= \pm \prod_{\mathcal{A}\in Part_{n}}(|\mathcal{A}|-1)!$$ tal que $|\mathcal{A}|$ es el número de clases de la partición $\mathcal{A}$. En particular, la matriz de conexidad es invertible. El siguiente Teorema es la fórmula de factorización buscada [1]J.M. Burgos, F. Robledo, Factorization of network reliability with perfect nodes I: Introduction and Statements, Discrete Applied Mathematics, Volume 198, 2016.:
Comentario heurístico: Es inevitable percibir el análogo estético de la fórmula anterior con la del elemento de central Casimir de un álgebra de Lie con generadores $R\big(G^{\mathcal{A}}\big)$ y constantes estructurales $a_{\mathcal{A}\mathcal{B}}$. La idea es atractiva ya que una fórmula de factorización debe ser invariante bajo la acción de ciertas perturbaciones. ¿Se podrá formalizar esta idea?
El caso $n=1$ es claro y reproduce la bien conocida fórmula de factorización por un vértice de articulación. Veamos el caso $n=2$. Ordenamos el conjunto de particiones $Part_{2}$ de la siguiente manera: $$Part_{2}= \{12, \overbrace{12}\}$$ y tenemos la matriz de conexidad: $$A_{2}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 1 \\ \end{array} \right)$$ Su inversa es: $$A_{2}^{-1}=\left(\begin{array}{cc} -1 & 1 \\ 1 & 0 \\ \end{array} \right)$$ Por el Teorema 4.1 tenemos la fórmula de factorización: $$R=R_{\hat{12}}\otimes R_{12} + R_{12}\otimes R_{\hat{12}} - R_{12}\otimes R_{12}$$. La Figura 7 muestra esta factorización.
Veamos el caso $n=3$. Ordenamos el conjunto de particiones $Part_{3}$ de la siguiente manera: $$Part_{3}= \{123, 1\overbrace{23}, \overbrace{13}2, \overbrace{12}3, \overbrace{123}\}$$ y tenemos la matriz de conexidad: $$A_{3}=\left( \begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ \end{array} \right)$$ Su inversa es: $$A_{3}^{-1}=\frac{1}{2}\left(\begin{array}{ccccc}1 & -1 & -1 & -1 & 2 \\ -1 & -1 & 1 & 1 & 0 \\ -1 & 1 & -1 & 1 & 0 \\ -1 & 1 & 1 & -1 & 0 \\ 2 & 0 & 0 & 0 & 0 \\ \end{array}\right)$$
Por el Teorema 4.1 tenemos la fórmula de factorización: \begin{eqnarray*} R &=& R_{\widehat{123}}\otimes R_{123} + R_{123}\otimes R_{\widehat{123}} +\frac{1}{2}\bigl(R_{123}\otimes R_{123}- R_{1\hat{23}}\otimes R_{1\hat{23}}- R_{\hat{13}2}\otimes R_{\hat{13}2} \\ & & -R_{\hat{12}3}\otimes R_{\hat{12}3} + R_{1\hat{23}}\otimes R_{\hat{13}2}+ R_{1\hat{23}}\otimes R_{\hat{12}3}+ R_{\hat{13}2}\otimes R_{\hat{12}3}- R_{123}\otimes R_{1\hat{23}} \\ & & - R_{123}\otimes R_{\hat{13}2}- R_{123}\otimes R_{\hat{12}3} + R_{\hat{13}2}\otimes R_{1\hat{23}}+ R_{\hat{12}3}\otimes R_{1\hat{23}}+ R_{\hat{12}3}\otimes R_{\hat{13}2}\bigr) \\ & & - R_{1\hat{23}}\otimes R_{123}- R_{\hat{13}2}\otimes R_{123}- R_{\hat{12}3}\otimes R_{123}. \end{eqnarray*} Esta fórmula está ilustrada en la Figura 11.

Al igual que en mecánica, podemos pensar a la teoría expuesta como un límite clásico de redes cuánticas. En estas redes ya no vale hipótesis hecha anteriormente de distribución independiente de las variables aleatorias. Esto se debe a la superposición de estados y los entrelazamientos resultantes. El espacio de estados será ahora un espacio vectorial complejo con base en los estados clásicos y con producto interno tal que los estados clásicos resulten ortonormales (estos estados pueden interpretarse también como campos). La posibilidad de factorización en el caso clásico se debe en escencia a la siguiente descomposición del espacio de estados: $$\{0,1\}^{E(G)}= \{0,1\}^{E(G_{1})\cup E(G_{2})}= \{0,1\}^{E(G_{1})}\times \{0,1\}^{E(G_{2})}$$ que en el caso cuántico se traduce en la siguiente: $$\mathbb{C}\big\langle \{0,1\}^{E(G)}\big\rangle= \mathbb{C}\big\langle \{0,1\}^{E(G_{1})}\big\rangle\otimes \mathbb{C}\big\langle \{0,1\}^{E(G_{2})}\big\rangle$$ El desarrollo de una teoría cuántica de las ideas antes expuestas es no trivial e interesante.
[1] J.M. Burgos, F. Robledo, Factorization of network reliability with perfect nodes I: Introduction and Statements, Discrete Applied Mathematics, Volume 198, 2016.
[2] J.M.Burgos, Factorization of network reliability with perfect nodes II: Connectivity matrix, Discrete Applied Mathematics, Volume 198, 2016.
[3] C.J. Colbourn, The Combinatorics of Network Reliability, New York, Oxford University Press, 1987.
[4] F. Moskovitz y R.A.D. Center, The analysis of redundancy networks, Rome Air Development Center, Air Research and Development Center, United States Air Force, 1958.
[5] N.L. Biggs, Algebraic Graph Theory, Cambridge University Press, Cambridge, 1993.
[6] A.Satyanarayana, M.Chang, Network Reliability and the Factoring Theorem, Networks, 13 (1983), 107-120.
[7] Yu.D. Burtin, B.G. Pittel, Asymptotic estimates of the reliability of a complex system, Engineering Cybernetics, 10 (1972), 445-451.
