Un baúl de problemas olvidado: parte V

Introducción

Esta es la quinta (y quizás penúltima) entrega de nuestro artículo sobre el “Baúl de Problemas” de la Miscelánea Matemática. En la primera sección del trabajo encontrarán las soluciones (o intentonas de solución) que, de los problemas planteados al final de la parte IV de este trabajo, hemos recibido; algunas de estas soluciones vienen acompañadas por comentarios adicionales que pudieran resultarles dignos de atención. En la sección Problemas propuestos se presentará una lista más de cinco problemas que pueden abordar en lo que aparece la próxima entrega del artículo: como de costumbre, estos problemas serán publicados en algún momento en El irracional y las soluciones más atractivas que en dicho sitio se recaben serán contempladas para formar parte de la siguiente entrega del artículo. ¡Esperamos empezar a leer sus soluciones en El irracional muy pronto!

Soluciones y comentarios

A continuación presentamos las soluciones (algunas de ellas acompañadas de comentarios adicionales) de los cinco problemas planteados al final de la parte IV de Un baúl de problemas olvidado. Entre estos problemas se encuentran las preguntas 15, 16 y 17 originalmente propuestas en “El Baúl de Problemas”. Cuando las soluciones presentadas se retoman de posts que pueden encontrarse en El irracional, lo mencionamos de manera explícita donde juzgamos prudente hacerlo. El planteamiento de los problemas para los cuales contamos con comentarios adicionales están precedidos por un *.

Problema 15, [8Miscelánea Matemática, 21, pág. 78.].

Solución.

Este problema fue resuelto en El irracional por Omar Antolín Camarena. Además, también nosotros teníamos preparada una solución para el problema. Presentaremos a continuación ambas soluciones, comenzando con la que nosotros teníamos contemplada.

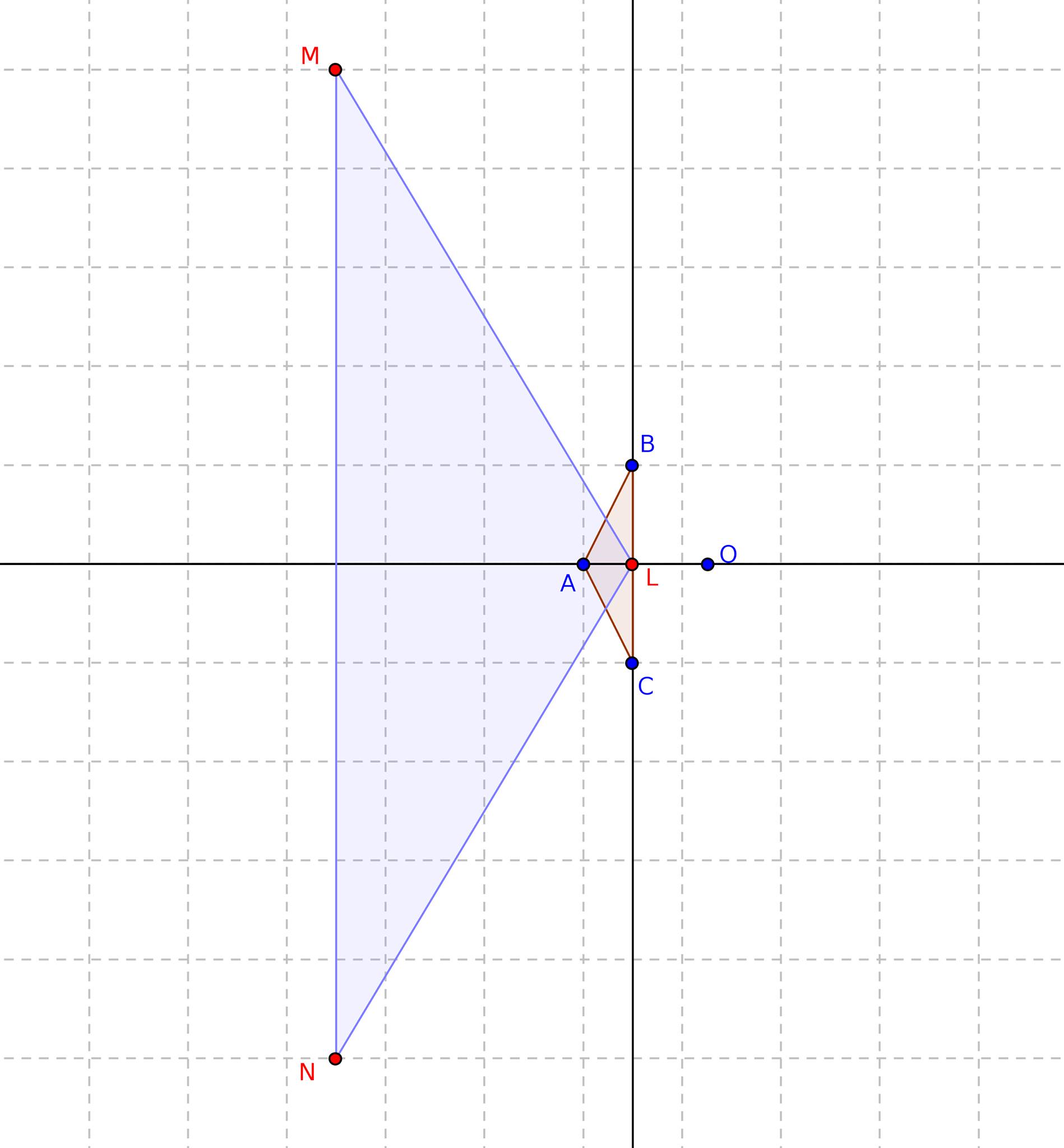
La respuesta es que no necesariamente se cumple la desigualdad en cuestión. A modo de (contra)ejemplo podemos considerar el triángulo $ABC$ en el plano cartesiano cuyos vértices son:

\[ A= (0,0), \quad B=(1,2) \quad \mbox{y} \quad C=(1,-2). \]

Se cumple entonces que el circuncentro $O$ de este triángulo se encuentra en $(\frac{5}{2},0)$. El punto de intersección de la recta que pasa por $A$ y $O$ con el lado $BC$ es $L=(1,0)$. El punto de intersección de la recta que pasa por $B$ y $O$ con el lado $AC$ es $M=(-5,10)$. El punto de intersección de la recta que pasa por $C$ y $O$ con el lado $AB$ es $N=(-5,-10)$. El área del triángulo $ABC$ es igual al valor absoluto de

\[ \frac{1}{2} \left|\begin{array}{ccc}0 & 0 & 1\\1 & 2 & 1\\1 & -2 & 1\end{array}\right| = -2 \]

y el área del triángulo $LMN$ es

\[ \frac{1}{2} \left|\begin{array}{ccc}1 & 0 & 1\\-5 & 10 & 1\\-5 & -10 & 1\end{array}\right| = 60. \]

Es claro que en este caso el área de $\triangle LMN$ es mucho mayor que el área de $\triangle ABC$. En la figura siguiente se esquematiza este contraejemplo: ¡la diferencia entre las áreas de uno y otro triángulo es en este caso más que evidente!

Por otro lado, es de notar que la respuesta es afirmativa si $ABC$ es un triángulo equilátero o $ABC$ es un triángulo rectángulo. De hecho, si $\triangle ABC$ es equilátero entonces $\triangle LMN$ también es equilátero y tiene por lado la mitad del lado de $\triangle ABC$. Por lo tanto, en este caso se cumple incluso que

\begin{align} \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle LMN = \frac{1}{4} \mbox{ } \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle ABC. \label{igualdad} \end{align}

Si $\triangle ABC$ es rectángulo con hipotenusa $CA$, entonces $O$ es el punto medio de $CA$. Así, en este caso se tiene que $L=C$, $M=O$ y $N=A$ y, por consiguiente,

\[ \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle LMN = 0. \]

Vamos a demostrar a continuación que la desigualdad es válida en cada triángulo acutángulo $ABC$, incluso si en lugar de $O$ se considera cualquier otro punto $P$ en el interior de $\triangle ABC$. La demostración se basará en un resultado que extiende al célebre teorema de Ceva.

El lector puede encontrar una demostración de este teorema en [3 N. M Beskin, División de un segmento en una razón dada. Serie: Lecciones Populares de Matemáticas, Ed. Mir, Moscú, 1976, págs. 77-78.]. El primer inciso del teorema es la parte que generaliza al teorema de Ceva, pues las tres cevianas concurren si y sólo si el área del triángulo que forman es $0$ si y sólo si $\lambda\mu\nu=1$.

El segundo inciso es el que permitirá establecer el problema que ahora nos ocupa. Consideremos el punto interior $P$ y construyamos el triángulo $\triangle LMN$. Por el teorema de Ceva tenemos que $\lambda\mu\nu=1$. Como $P$ es un punto interior al triángulo $ABC$, se sigue que $\lambda$, $\mu$ y $\nu$ son números reales positivos. Aplicando la desigualdad entre la media geométrica y la media aritmética se obtiene que

\begin{eqnarray*} 1 = \sqrt{\lambda\mu\nu} = \sqrt{\lambda}\cdot \sqrt{\mu}\cdot\sqrt{\nu} \leq \frac{\lambda+1}{2}\cdot \frac{\mu+1}{2}\cdot\frac{\nu+1}{2}, \end{eqnarray*}

o, equivalentemente,

\begin{eqnarray*} \frac{2}{(\lambda+1)(\mu+1)(\nu+1)} \leq \frac{1}{4}. \end{eqnarray*}

De esta última desigualdad y el segundo inciso del teorema de Routh se desprende que

\begin{eqnarray} \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle LMN &=& \frac{\lambda\mu\nu+1}{(\lambda+1)(\mu+1)(\nu+1)} (\mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle ABC) \nonumber\\ &=& \frac{2}{(\lambda+1)(\mu+1)(\nu+1)} (\mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle ABC) \nonumber \\ &\leq & \frac{1}{4} \mbox{ } \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle ABC, \label{objective} \end{eqnarray}

tal como se pretendía mostrar.

▢

Por supuesto, en el contraejemplo presentado la desigualdad entre la media geométrica y la media aritmética no aplica pues, al ser $O$ un punto exterior al triángulo $ABC$, no se tiene la positividad de $\lambda$, $\mu$ y $\nu$.

Finalmente, una observación sobre la igualdad

\begin{eqnarray*} \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle LMN = \frac{1}{4} \mbox{ } \mathsf{\acute{a}rea} \mbox{ } \mathsf{de} \mbox{ } \triangle ABC \label{igualdad2} \end{eqnarray*}

Si $ABC$ es un triángulo acutángulo y $\lambda$, $\mu$ y $\nu$ son como en la demostración de (\ref{objective}), entonces la igualdad en (\ref{objective}) se da cuando $\lambda=\mu=\nu=1$. Esto implica que $L$, $M$, $N$ son los puntos medios de los lados $AB$, $BC$ y $CA$, respectivamente. En consecuencia, $O$ es simultáneamente el circuncentro y baricentro de $\triangle ABC$. De esto se desprende a su vez que $\triangle ABC$ es equilátero. Así, los únicos triángulos acutángulos $ABC$ para los cuales se da la igualdad en (\ref{objective}) son los triángulos equiláteros.

Ahora mostraremos cómo es que, utilizando coordenadas baricéntricas, Omar Antolín Camarena demostró la desigualdad en el caso en el que $\triangle ABC$ es acutángulo:

Coloquemos el triángulo $ABC$ en el plano $z=1$ y usemos $A$ para denotar tanto el punto $A$ como el vector que va del origen a $A$, etc. Si $A \wedge B \wedge C$ denota el determinante de la matriz de $3 \times 3$ con columnas $A$, $B$ y $C$, entonces el área del triángulo $ABC$ es $\frac{1}{2} |A \wedge B \wedge C|$. (Éste es el motivo por el cual conviene hacer este problema de geometría plana con coordenadas en $\mathbb{R}^3$.)

Por otro lado, es sabido que cualquier punto $P$ en el plano de $ABC$ se puede escribir como $P = \frac{uA + vB + wC}{u+v+w}$ para algunos $u,v,w \in \mathbb{R}$; más aún, si $P$ está en el interior del triángulo, entonces se cumple que $u, v, w> 0$. A $u, v, w$ se les denomina las coordenadas baricéntricas de $P$. Usaremos la notación $(u:v:w)$ para referirnos tanto a las coordenadas baricéntricas como al punto que representan.

Supongamos que las coordenadas baricéntricas del circuncentro $O$ son $(u:v:w)$. Vamos a justificar que el punto $L$, como está definido en el enunciado del problema, tiene coordenadas baricéntricas $(0:v:w) = \frac{vB+wC}{v+w}$. En efecto, el punto con coordenadas baricéntricas $(0:v:w)$ está sobre $BC$ y reescribiendo $O = \frac{uA + (v+w) (0:v:w)}{u+v+w}$, notamos que $O$, $A$ y $(0:v:w)$ son colineales. De esta forma, $(0:v:w)$ es el punto de intersección de la recta $BC$ y la recta $OA$, y por lo tanto es $L$. Análogamente se justifica que $M=(u:0:w)$ y que $N=(u:v:0)$.

Ahora bien, apelando a propiedades básicas de los determinantes, llegamos a que \begin{eqnarray*}L \wedge M \wedge N &=& \frac{(vB+wC) \wedge (uA + wC) \wedge (uA+vB)}{(v+w)(u+w)(u+v)}\\ &=& \frac{2uvw}{(u+v)(u+w)(v+w)} A \wedge B \wedge C.\end{eqnarray*}

Tenemos así que la razón de las áreas de $LMN$ y $ABC$ es $$\theta := \frac{2uvw}{(u+v)(u+w)(v+w)}.$$ Como $\triangle ABC$ es acutángulo, entonces $u,v,w > 0$: luego, al multiplicar la desigualdad $\frac{u+v}{2} \ge \sqrt{uv}$ con las análogas para $u,w$ y $v,w$ se obtiene que $$\theta \le \frac{1}{4}.$$ La igualdad se da si y sólo si $u=v=w$, o sea, sólo cuando $O$ es simultáneamente el baricentro y circuncentro de $ABC$ (esto es, si y sólo si $ABC$ es un triángulo equilátero).

Podemos verificar nuevamente que la hipótesis de que $ABC$ es acutángulo es fundamental. Es conocido que las coordenadas baricéntricas del circuncentro son $(\sin 2\alpha : \sin 2\beta : \sin 2\gamma)$, donde $\alpha, \beta, \gamma$ son los ángulos interiores de $ABC$ en $A$, $B$ y $C$ respectivamente. Cuando $\alpha$ y $\beta$ difieren en $90$ grados, el factor $u+v=\sin 2\alpha + \sin 2\beta$ en el denominador de la fracción que define a $\theta$ es $0$. De esta forma, cuando el triángulo $ABC$ es obtusángulo, $\theta$ puede ser arbitrariamente grande (pues, en tal caso, los ángulos $\alpha$ y $\beta$ pueden elegirse de tal modo que la diferencia $\alpha-\beta$ sea cercana a 90 grados).

▢

Problema 16, [9Miscelánea Matemática, 22, pág. 78.].

Solución.

Recibimos dos soluciones para este problema en El irracional: una de ellas es de la autoría de Malors Espinosa y la otra de Omar Antolín Camarena.

Comenzaremos exponiendo la solución de Malors Espinoza. Por cuestiones de espacio, sólo esbozaremos esta demostración. El lector interesado en conocer todos los detalles puede revisar la solución completa en el thread de El irracional asociado a este problema.

Esbozo de la solución de Malors Espinosa. Definamos la función $$f(x):=\sum_{k = -\infty}^{\infty} 2^k \left\|\frac{x}{2^k}\right\|^{2}.$$ La respuesta se tendrá una vez que se hayan ejecutado los cuatro pasos siguientes:

1. Demostrar que la función $f$ es continua.
2. Encontrar el valor de la función $f$ en los números enteros.
3. Utilizar algunas propiedades de $f$ para hallar su valor en un conjunto $D$.
4. Mostrar que $D$ es un subconjunto denso de los números reales.

Estos pasos son suficientes para terminar el problema pues, a partir de la continuidad de $f$ y de los valores que ella asume en un subconjunto denso de $\mathbb{R}$, es posible conocer los valores que la función $f$ asume en todos los números reales.

Paso 1: Demostrar que la función $f$ es continua.

Para establecer que la función $f$ es continua se tiene que mostrar que $|f(x)-f(y)|$ se hace arbitrariamente pequeño conforme $|x-y|$ se hace pequeño. Para esto procedemos como sigue: \begin{align*} |f(x)-f(y)|&=\left|\sum_{k = -\infty}^{\infty} 2^k \left(\left\|\frac{x}{2^k}\right\|^{2}-\left\|\frac{y}{2^k}\right\|^{2}\right)\right|\\ &\leq \sum_{k = -\infty}^{\infty} 2^k \left|\left\|\frac{x}{2^k}\right\|^{2}-\left\|\frac{y}{2^k}\right\|^{2}\right|. \end{align*}

Queremos acotar esta suma. Para entenderla mejor, la dividiremos en $3$ partes.

1. Si $k$ es positivo y suficientemente grande, entonces el entero más cercano a $\frac{x}{2^k}$ es cero. Si además $y$ es cercano a $x$, entonces el entero más cercano a $ \frac{y}{2^k}$ también es cero. Estas observaciones permiten dar una cota para la cola de la suma en términos de $|x-y|$.

2. Tras acotar la cola de la suma, restan algunos términos que corresponden a $k$'s positivas. Como son una cantidad finita, basta con entenderlos uno por uno. De nuevo, si $x$ y $y$ son cercanos, entonces su entero más cercano es el mismo. Esto ayuda a realizar las manipulaciones algebraicas necesarias para dar las cotas deseadas.

3. Finalmente, acotamos los términos que corresponden a valores negativos de $k$. Para ello observamos que $\left\|\frac{x}{2^k}\right\|\lt 1$, y entonces \[ \sum_{k = 0}^{\infty} 2^{-k} \left\|\frac{x}{2^{-k}}\right\|^{2}\leq \sum_{k = 0}^{\infty} 2^{-k} = 2. \] Esto muestra que la parte de la serie de $f(x)$ correspondiente a valores negativos de $k$ converge. Debido a esto, la cola de esta serie se hace tan pequeña como se desee. A partir de aquí se deduce que la cola de $|f(x)-f(y)|$ correspondiente a valores negativos de $k$ se puede acotar en términos de $|x-y|$. El resto de los términos que corresponden a $k$'s negativas se acotan de manera análoga a como se hizo con los términos en los que $k$ era positiva.

Paso 2: Encontrar el valor de la función $f$ en los números enteros.

Tomemos un entero $N$. Primero notemos que los términos con $k$ negativa en la serie que define a $f(N)$ son todos cero, pues $2^kN \in \mathbb{Z}$ en tales casos. De esta forma, basta determinar la suma para los valores no negativos de $k$.

Escribamos a $N$ en su expansión binaria: $N=\sum_{j=-\infty}^\infty a_j 2^j$. Por supuesto, varios de los coeficientes $a_j$ son iguales a cero, pero es conveniente usar esta notación. Para cada entero no negativo $k$, escribamos a $N$ de la siguiente forma usando el algoritmo de la división

\[ N=A_k2^k+r_k,\quad 0\leq r_j<2^k. \]

Una observación fundamental es que el entero más cercano a $\frac{N}{2^k}$ depende del dígito binario $a_{k-1}$, pues este dígito nos dice si en un intervalo entre números enteros consecutivos el número queda antes o después de la mitad del intervalo. Siendo más específicos, a partir de la notación que hemos establecido se puede mostrar que:

\[ \left\|\frac{N}{2^k}\right\|^2=\left(a_{k-1}-\frac{r_k}{2^k}\right)^2. \]

Esto nos da la siguiente expresión para $f$:

\[ f(N) = \sum_{k = 0}^{\infty}2^k\left(a_{k - 1} - \dfrac{r_k}{2^k}\right)^2. \]

A partir de esta expresión es fácil conjeturar que para $N \in \mathbb{Z}^{+}$ se cumple que $f(N)=N$. Del mismo modo, esta expresión resulta útil al momento de demostrar la conjetura. Finalmente, puesto que $\left\|\frac{-N}{2^k}\right\|=\left\|\frac{N}{2^k}\right\|$, se tiene que $f(-N)=f(N)=N$. Concluimos de todo lo anterior que $f(N)=|N|$ para cada $N \in \mathbb{Z}$.

Paso 3: Utilizar algunas propiedades de $f$ para hallar su valor en un conjunto $D$.

Si $x \in \mathbb{R}$:

\begin{align} \label{igual} f(2x) = \sum_{k=-\infty}^\infty 2^k \left\|\frac{2x}{2^k} \right\|^2 = 2 \sum_{k=-\infty}^\infty 2^{k-1} \left\|\frac{x}{2^{k-1}} \right\|^2 = 2f(x) \end{align}

Esta igualdad nos permite "sacar factores $2$". Consideremos el conjunto $D:=\left\{\frac{m}{2^n}:m,n\in\mathbb{Z}\right\}$. Aplicando repetidas veces la igualdad $(\ref{igual})$ y usando que $f(x)=|x|$ para $x \in \mathbb{Z}$, obtenemos que $f(x)=|x|$ para cualquier $x\in D$.

Paso 4: Mostrar que $D$ es un subconjunto denso de los números reales.

Para ver que $D$ es denso basta que mostremos que hay un elemento de $D$ en cualquier intervalo de los reales. Tomemos un intervalo de longitud $\epsilon$. Si tomamos $n$ de modo que $\frac{1}{2^n} < \epsilon$, cada que aumentamos $m$ en uno el número $\frac{m}{2^n}$ aumenta en menos que $\epsilon$. Por lo tanto, al variar $m$ en todos los enteros alguno de los números de $D$ pertenecerá al intervalo en consideración.

Así pues, al haberse establecido que $f$ es continua y que $f(x)=|x|$ para todo $x$ en $D$, el cual es un subconjunto denso de los números reales, se concluye que $f(x)=|x|$ para todo número real $x$.

▢

A continuación presentamos la solución de Omar Antolín Camarena. Si bien es una solución que depende de varias cuentas, Omar estudia primeramente el comportamiento de la función $f$ en el intervalo $[0,1]$ y, luego, extrapola lo que en dicho intervalo obtiene a todo el dominio de $f$ usando la identidad en $(\ref{igual})$.

Solución de Omar Antolín Camarena. Supongamos primero que $0 \le x \le 1$.

Para $k>0$, tenemos $0 \le \frac{x}{2^k} \le \frac{1}{2}$, de modo que $\left\| \frac{x}{2^k} \right\| = \frac{x}{2^k}$. Entonces,

\[ f_+(x) := \sum_{k>0} 2^k \left\|\frac{x}{2^k} \right\|^2 = \sum_{k>0} \frac{x^2}{2^k} = x^2. \]

Sólo falta calcular $f_-(x) := \sum_{k \le 0} 2^k \left\|\frac{x}{2^k} \right\|^2 = \sum_{k \ge 0} 2^{-k} \left\| 2^k x \right\|^ 2$. Para eso usaremos la expansión binaria de $x$. Supongamos que $x = \sum_{j>0} a_j 2^{- j}$ donde cada $a_j$ es $0$ o $1$.

Para $k>0$, la parte fraccionaria de $2^k x$ es $\{2^k x\} = \sum_{j>k} a_j 2^{k-j}$. Si $a_{k+1} = 0$, esta parte fraccionaria es menor o igual a $\frac{1}{2}$ y, en consecuencia, $$\left\| 2^k x \right\| = \{2^k x\} = \sum_{j>k+1} a_j 2^{k-j}.$$ Si $a_{k+1} = 1$, entonces $$\left\| 2^k x \right\| = 1 - \{2^x k\} = - \sum_{j>k+1} a_j 2^{k-j} + \frac{1}{2}.$$ Una fórmula que cubre ambos casos es $$\left\| 2^k x \right\| = \left| \sum_{j>k+1} a_j 2^{k-j} - \frac{1}{2}a_{k+1} \right|.$$

Así pues, tenemos que $$f_-(x) = \sum_{k \ge 0} 2^{-k} \left( \sum_{j>k+1} a_j 2^{k-j} - \frac{1}{2}a_{k+1} \right)^2.$$ Desarrollando el cuadrado obtenemos $$f_-(x) = \sum_{k \ge 0} a_{k+1} 2^{-k-2} - \sum_{k \ge 0} \sum_{j>k+1} a_j a_{k+1} 2^{-j} + \sum_{k \ge 0} 2^k \left( \sum_{j>k+1} a_j2^{-j} \right)^2.$$

Llamémosle a esas tres sumas $A(x), B(x)$ y $C(x)$, respectivamente. Se cumple entonces que $f_-(x) = A(x) - B(x) + C(x)$. Además, resulta fácil convencerse de que $A(x) = \frac{1}{2} x$.

Simplificamos $B(x)$ haciendo $l=k+1$: $B(x) = \sum_{l>0} \sum_{j>l} a_j a_l 2^{-j}$.

Para calcular $C(x) = \sum_{k \ge 0} 2^k Q_k$, expandimos el cuadrado que ocurre ahí: $$Q_k := \left( \sum_{j>k+1} a_j2^{-j} \right)^2 = \sum_{j>k+1} a_j 2^{-2j} + 2 \sum_{l>k+1} \sum_{j>l} a_j a_l 2^{-j-l}.$$

Entonces: $$C(x) = \sum_{k \ge 0} \sum_{j>k+1} a_j 2^{k-2j} + 2 \sum_{k \ge 0} \sum_{l>k+1}\sum_{j>l} a_j a_l 2^{k-j-l} =: C_1(x) + C_2(x).$$

Calculamos cada $C_i(x)$ por separado: $$ C_1(x) = \sum_{j>1} a_j 2^{-2j} \sum_{k=0}^{j-2} 2^k = \sum_{j>1} a_j 2^{-2j} (2^{j-1} - 1) = \frac{1}{2} x - \sum_{j>0} a_j 2^{-2j}$$

y

$$C_2(x) = 2 \sum_{l>1} \sum_{j>l} a_j a_l 2^{-j-l} \sum_{k=0}^{l-2} 2^k = \sum_{l>0}\sum_{j>l} a_j a_l 2^{-j-l} (2^l-2).$$

De modo que $C_2(x) = B(x) - 2 \sum_{l>0}\sum_{j>l} a_j a_l 2^{-j-l}$. Por lo tanto, $$C(x) = \frac{1}{2} x + B(x) - \sum_{j>0} a_j 2^{-2j} - 2\sum_{l>0} \sum_{j>l} a_j a_l 2^{-j-l} = \frac{1}{2} x + B(x) - x^2.$$

Juntando todo obtenemos que $f_-(x) = A(x)-B(x)+C(x) = x-x^2$ y, por consiguiente, $f(x) = f_+(x) + f_-(x) = x$ para toda $x \in [0,1]$.

Finalmente, como $\left\|y\right\| = \left\|-y\right\|$, tenemos que $f(x)=f(-x)$. Además, para cada $x \in \mathbb{R}$ se observa también que $$f(2x) = \sum_{k=-\infty}^\infty 2^k \left\|\frac{2x}{2^k} \right\|^2 = 2 \sum_{k=-\infty}^\infty 2^{k-1} \left\|\frac{x}{2^{k-1}} \right\|^2 = 2f(x).$$ Estas dos relaciones implican que $f(x) = |x|$ para todo $x$.

▢

* Problema 17, [9Miscelánea Matemática, 22, pág. 78.].

Solución.

P. Gattei da con una solución en [5P. Gattei, The "inverse" differential equation. Mathematical Spectrum, 4 (23), págs. 127-131.] suponiendo que para cada $x \in [0,\infty)$, $f(x)=Ax^{n}$ (donde $A$ y $n$ son constantes positivas). En tal caso se tiene que $f^{\prime}(x) = Anx^{n-1}$ y $f^{-1}(x)=(x/A)^{1/n}$ y la condición $f^{\prime}(x) = f^{-1}(x)$ deviene entonces en \begin{eqnarray*} Anx^{n-1}= \left(\frac{x}{A}\right)^{\frac{1}{n}}, \end{eqnarray*} o, equivalentemente, en \begin{eqnarray*} A^{n+1}n^{n}x^{n(n-1)} = x. \end{eqnarray*} De esto se sigue que $n$ es tal que $n^{2}-n-1=0$ y $A^{n+1}n^{n}=1.$ Resolviendo la ecuación cuadrática en $n$ se obtiene que $n$ es igual a $\phi$ o $n$ es igual a $1-\phi$ donde $\phi = \frac{1+\sqrt{5}}{2}$ es la razón áurea. Puesto que \begin{eqnarray*} A = n^{-\frac{n}{n+1}}, \end{eqnarray*} el caso $n=1-\phi$ se desecha y se concluye que una solución para el problema de valor inicial en cuestión está dada por \begin{eqnarray*} f(x)= \phi^{-\frac{\phi}{\phi+1}}x^{\phi}. \end{eqnarray*}

▢

Omar Antolín Camarena llegó al mismo resultado en un comentario que puede encontrarse en el thread de El irracional correspondiente a esta pregunta. Lo que resta por determinar es si la solución del problema es única o no. Por la forma en que el problema está planteado se podría pensar que, aparte de la solución obtenida, no habría otra más: sin embargo, esto podría apuntar también a una simple falta de previsión por parte de quien inicialmente propusó el problema en la Miscelánea Matemática. ¿Qué opina usted sobre este asunto, estimado lector?

* Problema IV de UBPO (parte IV).

Solución.

Presentaremos a continuación la solución que Malor Espinosa tuvo a bien compartirnos en el thread respectivo de El irracional.

Para cada $N \in \mathbb{N}$, denotemos con $a_N$ a la cantidad de números totalmente primos de $N$ dígitos. Así pues, si $n \in \mathbb{N}$ y $Q$ es un número de $n+1$ dígitos que es totalmente primo, entonces el número conformado por los primeros $n$ dígitos de $Q$ también es totalmente primo; además, como $Q$ es, en particular, un número primo, el dígito de las unidades de $Q$ pertenece necesariamente al conjunto $\{1,3,7,9\}$. De esto se sigue que la cantidad de números totalmente primos de $n+1$ dígitos es a lo más $4$ veces la cantidad de números totalmente primos de $n$ dígitos: esto es, para cada $n \in \mathbb{N}$ se tiene que $$a_{n+1} \leq 4a_{n}.$$

De lo anterior y del hecho que hay exactamente $4$ números totalmente primos de un dígito se sigue que $$a_{n+1} \leq 4^{n}a_{1} = 4^{n+1}$$ para cada $n \in \mathbb{Z}^{+}.$

Ahora bien, denotemos con $\mathbb{b}_{j}$ al $j$-ésimo número totalmente primo y con $b_{j}^{(k)}$ al $j$-ésimo totalmente primo de $k$ dígitos. Puesto que para cada $M \in \mathbb{N}$ se cumple que \begin{eqnarray*}\sum_{j=1}^{M}\frac{1}{\mathbb{b}_{j}} &\leq& \sum_{j=1}^{a_{1}} \frac{1}{b_{j}^{(1)}} + \sum_{j=1}^{a_{2}} \frac{1}{b_{j}^{(2)}} + \sum_{j=1}^{a_{3}} \frac{1}{b_{j}^{(3)}} + \cdots\\ &\leq& a_{1} + \frac{a_{2}}{10} + \frac{a_{3}}{10^{2}} + \cdots \\ &\leq& \sum_{n=1}^{\infty} \frac{4^{n}}{10^{n-1}}\\ &=& \frac{20}{3}, \end{eqnarray*} tenemos que la sucesión de sumas parciales de la serie de los recíprocos de los números totalmente primos es creciente y acotada; consiguientemente, la serie en cuestión es convergente.

▢

Otra manera de establecer la convergencia de la serie de los recíprocos de los números totalmente primos es notando que el conjunto de números de tal índole es finito. De acuerdo con la rutina de Mathematica^® que se muestra en el recuadro de abajo, en el intervalo $[10^{7}, 10^{8})$ sólo hay $5$ números totalmente primos: a saber, $23 \, 399 \, 339, 29 \, 399 \, 999, 37 \, 337 \, 999, 59 \, 393 \, 339$ y $73 \, 939 \, 133$.

Luego, al tenerse que \begin{eqnarray*} 233 \, 993 \, 39\mathbf{1} &=& 3 \times 97 \times 733 \times 1 \, 097,\\ 233 \, 993 \, 39\mathbf{3} &=& 193 \times 1 \, 212 \, 401,\\ 233 \, 993 \, 39\mathbf{7} &=& 3 \times 11 \times 73 \times 137 \times 709,\\ 233 \, 993 \, 39\mathbf{9} &=& 173 \times 409 \times 3 \, 307,\\ \\ 293 \, 999 \, 99\mathbf{1} &=& 3 \times 101 \times 970 \, 297,\\ 293 \, 999 \, 99\mathbf{3} &=& 7 \times 47 \times 167 \times 5 \, 351,\\ 293 \, 999 \, 99\mathbf{7} &=& 3 \times 191 \times 241 \times 2 \, 129,\\ 293 \, 999 \, 99\mathbf{9} &=& 29 \times 10 \, 137 \, 931,\\ \\ 373 \, 379 \, 99\mathbf{1} &=& 3 \times 79 \times 1 \, 575 \, 443,\\ 373 \, 379 \, 99\mathbf{3} &=& 7 \times 17 \times 139 \times 22 \, 573,\\ 373 \, 379 \, 99\mathbf{7} &=& 3 \times 5923 \times 21 \, 013,\\ 373 \, 379 \, 99\mathbf{9} &=& 23 \times 131 \times 123 \, 923,\\ \\ 593 \, 933 \, 39\mathbf{1} &=& 3^{4} \times 7 \, 332 \, 511,\\ 593 \, 933 \, 39\mathbf{3} &=& 23 \times 61 \times 173 \times 2 \, 447,\\ 593 \, 933 \, 39\mathbf{7} &=& 3 \times 197 \, 977 \, 799,\\ 593 \, 933 \, 39\mathbf{9} &=& 11 \, 941 \times 49 \, 739,\\ \\ 739 \, 391 \, 33\mathbf{1} &=& 3 \times 7^{2} \times 167 \times 30 \, 119,\\ 739 \, 391 \, 33\mathbf{3} &=& 127 \times 5 \, 821 \, 979,\\ 739 \, 391 \, 33\mathbf{7} &=& 3^{2} \times 29 \times 2 \, 832 \, 917,\\ 739 \, 391 \, 33\mathbf{9} &=& 9 \, 521 \times 77 \, 659,\\ \end{eqnarray*} se desprende que no existe un número totalmente primo de $9$ o más dígitos. Ergo, ¡el cardinal del conjunto conformado por los números totalmente primos es menor que $10^{8}$! De hecho, de acuerdo con la misma rutina de Mathematica^® presentada líneas arriba, el cardinal exacto del conjunto de números naturales que son totalmente primos es $83$: esta cifra está en concordancia con lo que sobre estos números puede encontrarse en la On-Line Encyclopædia of Integer Sequences del Prof. Neil J. Sloane y cía. (cf. [7N. J. Sloane, The On-Line Encyclopædia of Integer Sequences. http://oeis.org, sequence A024770.]). Estas consideraciones dan lugar a la muy natural cuestión siguiente:

¿Será posible dar una demostración a priori y simple de la finitud del conjunto de números naturales que son totalmente primos? A priori, en el sentido de que no se base en el hecho de que el mayor número totalmente primo es menor que $10^8$; simple, en el sentido de que no apele intensamente a cálculos en Mathematica^® (o algún otro sistema de álgebra computacional).

¡Estaremos al tanto de cualquier mensaje que sobre sus cavilaciones en torno a esta última pregunta tengan a bien hacernos llegar!

* Problema V de UBPO (parte IV).

Solución.

Si $|G|=1$, el aserto claramente tiene lugar. Así pues, en lo sucesivo podemos suponer que $|G|>1$ y que $|G| = p_{1}^{a_{1}}p_{2}^{a_{2}} \cdots p_{n}^{a_{n}}$, donde $p_{1} < p_{2} < \cdots < p_{n}$ son números primos y $a_{i} \in \mathbb{N}$ para todo $i \in \{1, \ldots, n\}$. Demostraremos la proposición haciendo inducción sobre $\omega(|G|)$, el número de factores primos distintos de $|G|$.

Si $\omega(|G|)=1$, entonces $|G| = p_{i}^{a_{i}}$ para algún $i \in \{1, \ldots, n\}$. Luego, si $N$ denota al total de subgrupos de Sylow de $G$ y $N_{p_{i}}$ al número de $p_{i}-$subgrupos de Sylow de $G$, entonces, del tercer teorema de Sylow (cf. [6, págs. 99-100I. N. Herstein, Topics in Algebra (2nd edition). Xerox College Publishing, Lexington, Massachusetts, USA, 1975.]) y del hecho de que $p_{i}^{a_{i}} \geq 2$, se sigue que \begin{eqnarray*} N = N_{p_{i}} = 1 \leq \frac{4}{3} \leq \left(\frac{2}{3}\right)p_{i}^{a_{i}} = \frac{2}{3}|G| \end{eqnarray*} tal como se deseaba establecer.

Suponiendo que el aserto también es válido para cualquier grupo $G$ tal que $\omega(|G|)=n-1$, demostrémoslo para cuando el número de factores primos de $|G|$ es $n$. En esta parte apelamos al siguiente análisis de casos:

1. $G$ contiene un $2-$complemento normal $H$: en este caso, $2 \mid |G|$ y, además, $N_{2} \leq \frac{|G|}{2}$. Si $N_{2} < \frac{|G|}{2}$, entonces se tiene de hecho que $N_{2} \leq \frac{|G|}{3}$. Además, para $i > 2$, los $p_{i}-$subgrupos de Sylow de $G$ coinciden con los $p_{i}-$subgrupos de Sylow de $H$. Como $\omega(|H|) = n-1$, la hipótesis de inducción nos permite concluir que el total de subgrupos de Sylow de $G$ es \begin{eqnarray*} N &=& N_{2} + \sum_{1< k \leq n} N_{p_{k}}\\ &\leq& \frac{|G|}{3} + \frac{2}{3}|H|\\ &=& \frac{|G|}{3} + \frac{2}{3}\left(\frac{|G|}{2^{a_{1}}}\right)\\ &\leq& \frac{|G|}{3} + \frac{|G|}{3}\\ &=& \frac{2}{3}|G|.\end{eqnarray*} Si $N_{2} = \frac{|G|}{2}$, entonces, al tenerse que $N_{2} \mid |G|$ y que $N_{2} \equiv 1 \pmod{2}$, se cumple que $|G| = 2 \cdot p_{2}^{a_{2}} \cdots p_{n}^{a_{n}}$. En consecuencia, $G$ es un grupo de orden par en el que la mitad de los elementos son de orden dos y la otra mitad conforma al subgrupo $H$ (de orden $p_{2}^{a_{2}} \cdots p_{n}^{a_{n}}$). En este escenario, al invocar el ejercicio 15 de [6, pág. 71I. N. Herstein, Topics in Algebra (2nd edition). Xerox College Publishing, Lexington, Massachusetts, USA, 1975.], obtenemos que $H$ es un subgrupo abeliano de $G$. Esto implica en particular que, para $i > 2$, los $p_{i}-$subgrupos de Sylow de $G$ son normales: por consiguiente, el total de subgrupos de Sylow de $G$ en este subcaso es \begin{eqnarray*} N = N_{2} + (n-1) = \frac{|G|}{2} + (n-1). \end{eqnarray*} De esto y del hecho de que \begin{eqnarray*} |G| = 2 \cdot p_{2}^{a_{2}} \cdots p_{n}^{a_{n}} \geq 2 \cdot 3^{n-1} \geq 2\cdot 3(n-1) \end{eqnarray*} se colige que \begin{eqnarray*} N \leq \frac{|G|}{2} + \frac{|G|}{6} = \frac{2}{3}|G|. \end{eqnarray*}

2. $G$ no contiene un $2-$complemento normal: en este caso, hay dos posibilidades a considerar.

   Si $G$ contiene un $3-$complemento normal $H$, entonces $\omega(|H|) = n-1$ y, además, con excepción de los $3-$subgrupos de Sylow de $G$, $H$ contiene a todos los $p-$subgrupos de Sylow de $G$. Luego, si $p_{i}$ es el primo que en la descomposición de $|G|$ corresponde al primo $3$, el total de subgrupos de Sylow de $G$ en este subcaso es \begin{eqnarray*} N &=& N_{3} + \sum_{k \neq i} N_{p_{k}}\\ &\leq& \frac{|G|}{3} + \frac{2}{3}|H|\\ &\leq& \frac{|G|}{3} + \frac{2}{3}\left(\frac{|G|}{3^{a_{i}}}\right)\\ &\leq& \frac{|G|}{3} + \frac{2}{3}\left(\frac{|G|}{3}\right)\\ &=& \frac{5}{9}|G|\\ &<& \frac{2}{3}|G|. \end{eqnarray*}

   Si $G$ no contiene un $3-$complemento normal, entonces el número de $2-$subgrupos y $3-$subgrupos de Sylow de $G$ los estimamos mediante el teorema de transferencia de Burnside (ver, por ejemplo, [4, pág. 99C. W. Curtis, Pioneers of Representation Theory: Frobenius, Burnside, Schur, and Brauer. American Mathematical Society & London Mathematical Society, 1999.]):
   
   Si $p_{1}=2$ y $P$ es un $2-$subgrupo de Sylow de $G$ entonces, al no contener $G$ un $2-$complemento normal, el teorema de transferencia de Burnside implica que $|N_{G}(P)| \geq 8$ y, en consecuencia, \begin{eqnarray*} N_{2} = [G:N_{G}(P)] = \frac{|G|}{|N_{G}(P)|} \leq \frac{|G|}{8} \label{sylow1}. \end{eqnarray*} Si $p_{2}=3$ y $Q$ es un $3-$subgrupo de Sylow de $G$, entonces el teorema de transferencia de Burnside implica que $|N_{G}(Q)| \geq 6$ y por consiguiente \begin{eqnarray*} N_{3} = [G:N_{G}(Q)] = \frac{|G|}{|N_{G}(Q)|} \leq \frac{|G|}{6} \label{sylow2}. \end{eqnarray*} De las estimaciones anteriores se desprende que el total de subgrupos de Sylow de $G$ es \begin{eqnarray} N &=& N_{2} + N_{3} + \sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} =1} N_{p_{i}} + \sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} \geq 2} N_{p_{i}} \nonumber\\ & \leq & \frac{|G|}{8} + \frac{|G|}{6}+\sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} =1} N_{p_{i}} + \sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} \geq 2} N_{p_{i}}. \label{sylow3}\\ \end{eqnarray} Para acotar superiormente la primera suma en (\ref{sylow3}) usamos el hecho de que, cuando $a_{i}=1$, $N_{p_{i}}$ es igual a la razón entre el número $\mathcal{O}_{p_{i}}$ de elementos de $G$ de orden $p_{i}$ y $p_{i}-1$: de esto se desprende que \begin{eqnarray} \sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} =1} N_{p_{i}} &=& \sum_{p_{i} \mid |G|, \, p_{i} \geq 5} \frac{\mathcal{O}_{p_{i}}}{p_{i}-1} \nonumber\\ &\leq& \frac{1}{4} \sum_{p_{i} \mid |G|, \, p_{i} \geq 5} \mathcal{O}_{p_{i}} \nonumber\\ &\leq& \frac{|G|}{4}. \label{sylow4} \end{eqnarray} Para acotar la segunda suma en (\ref{sylow3}) notamos que, como consecuencia del tercer teorema de Sylow, se tiene que si $p_{i} \geq 5$ es un número primo que en la descomposición canónica de $|G|$ aparece con un exponente $a_{i}\geq 2$ entonces \begin{eqnarray*} N_{p_{i}} \leq \frac{|G|}{p^{2}} \end{eqnarray*} y, consecuentemente, \begin{eqnarray} \sum_{p_{i} \mid |G|, \, p_{i} \geq 5, \, a_{i} \geq 2} N_{p_{i}} &\leq& \sum_{p \in \mathbf{P}} \frac{|G|}{p^{2}} - \frac{|G|}{4} - \frac{|G|}{9} \label{sylow5} \\ \end{eqnarray} donde $\mathbf{P}$ denota al subconjunto de $\mathbb{N}$ constituido por los números primos. De (\ref{sylow3}), (\ref{sylow4}) y (\ref{sylow5}) y, puesto que $\zeta(2) = \sum_{n=1}^{\infty} \frac{1}{n^{2}} = \frac{\pi^{2}}{6}$ (en [1, págs. 53-60M. Aigner y G. M. Ziegler, Proofs from THE BOOK (5th edition). Springer-Verlag Berlin/Heildelberg, 2014.] pueden encontrarse tres ingeniosas demostraciones de este célebre resultado), se concluye que \begin{eqnarray*} N &\leq& \frac{|G|}{8} + \frac{|G|}{6}+\frac{|G|}{4}+\left(\frac{\pi^{2}}{8} - \frac{3}{4}\right)|G| - \frac{|G|}{4} - \frac{|G|}{9}\\ &=& \left(\frac{\pi^{2}}{8}-\frac{41}{72}\right)|G|\\ &<& \left(\frac{1}{8}\left(\frac{22}{7}\right)^{2} - \frac{41}{72}\right)|G|\\ &=& \frac{2347}{3528} |G|\\ &<& \frac{2}{3}|G|\\ \end{eqnarray*}

Puesto que el análisis efectuado ha sido exhaustivo, el establecimiento del paso de inducción ha culminado y, con ello, también la demostración.

▢

El problema anterior apareció en la columna de problemas del American Mathematical Monthly correspondiente al número de agosto-septiembre de 2015. Fue contribuido por el Prof. Keith Kearnes del Depto. de Matemáticas de la Universidad de Colorado; la solución arriba expuesta se debe, esencialmente, al usuario Matt Samuel de math.stackexchange.com.

Problemas propuestos

Presentamos a continuación una lista de problemas en los que el lector puede meditar en lo que llega la entrega número seis de nuestro artículo. Estos cinco problemas se subirán, a su debido momento, a El irracional, donde será posible comentarlos y/o resolverlos. Como se mencionó en la introducción del artículo, las soluciones más atractivas que en dicho sitio se recolecten podrían ser incluidas en una entrega venidera de Un Baúl de Problemas Olvidado.

1. (Problema 18, Misc. Matemática #22, pág. 78.) En el tetraedro ABCD, las bisectrices de los ángulos ADB y ACB concurren en un punto de la arista AB. Demuestre que las bisectrices de los ángulos DAC y DBC concurren en un punto de la arista CD.

2. (Problema 19, Misc. Matemática #22, pág. 78.) Encuentre los siguientes límites: \begin{eqnarray*} \lim_{x \to 0^{+}} x, \lim_{x \to 0^{+}} x^{x}, \lim_{x \to 0^{+}} x^{x^{x}}, \lim_{x \to 0^{+}} x^{x^{x^{x}}}, \ldots \end{eqnarray*}

3. (Selectivo B (2016) de la Facultad de Ciencias de la UNAM para la IMC) Sea $n$ un entero mayor que $1$. Sea $V=\mathbb{C}^n$ el espacio vectorial complejo de dimensión $n$. Considere la transformación lineal $\phi:V\to V$ dada por: \[\phi(x_1,x_2,\ldots,x_{n-1},x_n) = (x_2,x_3,\ldots,x_n,x_1)\]

   • Encuentre los eigenvalores de $\phi$ y una base ortogonal de $V$ de eigenvectores de $\phi$.

   • Sean $a_1$, $a_2$, $a_3$, $a_4$, $a_5$ cinco reales tales que \begin{align*} a_1+a_2+a_3+a_4+a_5&=0\\ a_1^2+a_2^2+a_3^2+a_4^2+a_5^2&=1 \end{align*} Determine el máximo valor que puede tener $$a_1a_2+a_2a_3+a_3a_4+a_4a_5+a_5a_1.$$

4. Sea $p$ un número primo. Demuestre que si $p \nmid abc$, entonces la congruencia $$ax^{3}+by^{3}+cz^{3} \equiv 0 \pmod{p}$$ tiene al menos una solución no trivial (i.e., una solución en la cual $x$, $y$, $z$ no son todos congruentes con $0$ módulo $p$).

5. (Problema 4, VI CIIM.) Sea $\{a_n\}_{n \in \mathbb{N}}$ una sucesión estrictamente creciente de enteros positivos. Denotemos con $[a_n,a_{n+1}]$ al mínimo común múltiplo de $a_n$ y $a_{n+1}$. Demuestre que la serie $$ \sum_{n=1}^\infty \frac{1}{[a_n,a_{n+1}]} $$ converge.

¡Hasta la próxima!

Referencias

[1] M. Aigner y G. M. Ziegler, Proofs from THE BOOK (5th edition). Springer-Verlag, Berlin/Heildelberg, 2014.

[2] T. M. Apostol, Introduction to Analytic Number Theory. Springer-Verlag, New York, 1976.

[3] N. M. Beskin, División de un segmento en una razón dada. Serie: Lecciones Populares de Matemáticas, Ed. Mir, Moscú, 1976.

[4] C. W. Curtis, Pioneers of Representation Theory: Frobenius, Burnside, Schur, and Brauer. American Mathematical Society & London Mathematical Society, 1999.

[5] P. Gattei, The "inverse" differential equation. Mathematical Spectrum, 4 (23), págs. 127-131.

[6] I. N. Herstein, Topics in Algebra (2nd edition). Xerox College Publishing, Lexington, Massachusetts, USA, 1975.

[7] N. J. Sloane, The On-Line Encyclopædia of Integer Sequences. http://oeis.org, sequence A024770.

[8] Miscelánea Matemática, 21.

[9] Miscelánea Matemática, 22.