

El problema de determinar cuáles son los polígonos o combinaciones de polígonos que pueden cubrir el plano sin superposiciones es uno de los más bellos de la matemática. A pesar de su formulación elemental, que permite que hasta el más inexperto investigador pueda trabajar en él, se trata de un problema complejo y profundo, con ramificaciones hacia varias líneas de la matemática y otras ciencias, y permanece aún abierto en muchas direcciones.
El tema atrajo obviamente la atención desde tiempos remotos. Por ejemplo, era muy conocido en la Antigüedad que, entre los polígonos regulares, solo los triángulos, cuadrados y hexágonos pueden embaldosar el plano, quedando imposibilitados los polígonos de más de seis lados por “razones de espacio” y el pentágono por ser un “caso exótico”. Más tarde, Johannes Kepler se interesó en determinar las combinaciones de distintos polígonos regulares que permiten cubrir el plano [9]Euclidean tilings by convex regular polygons, artículo de Wikipedia..
El problema se vuelve más interesante cuando se considera polígonos irregulares, siendo ya el caso de los polígonos convexos suficientemente complejo. En esta dirección, en 1978, Ian Niven [6]I. Niven. Convex polygons that cannot tile the plane. American Math. Monthly 54 (1978), 785-792. dio una sencilla y hermosa demostración de que ningún conjunto finito de polígonos convexos de más de seis lados puede embaldosar el plano. De hecho, el resultado de Niven se aplica a conjuntos infinitos siempre que estos no incluyan sucesiones de polígonos cuya geometría “degenere”, haciéndose cada vez más “achatados”.
Restrinjamos, entonces, la discusión a embaldosados por un único polígono de no más de seis lados. Como se observa más abajo, cualquier triángulo cubre el plano si se lo dispone de manera astuta. Lo mismo sucede con cualquier cuadrilátero, sea convexo o no.
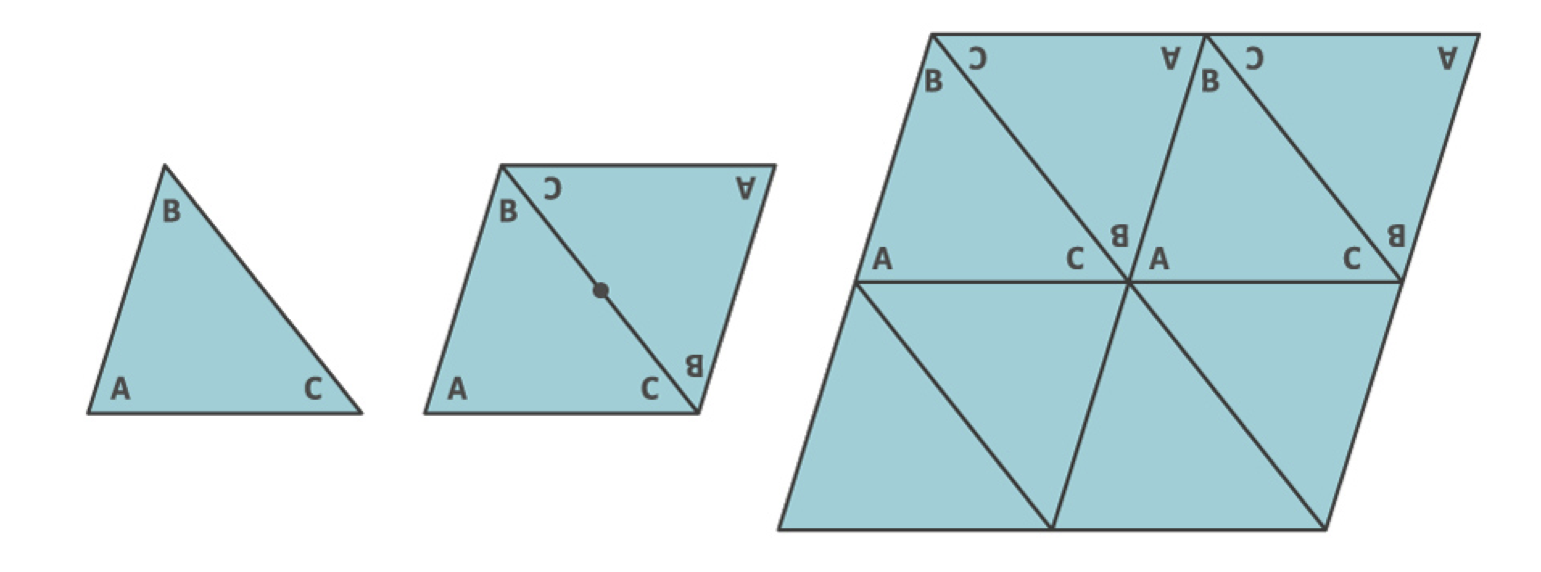
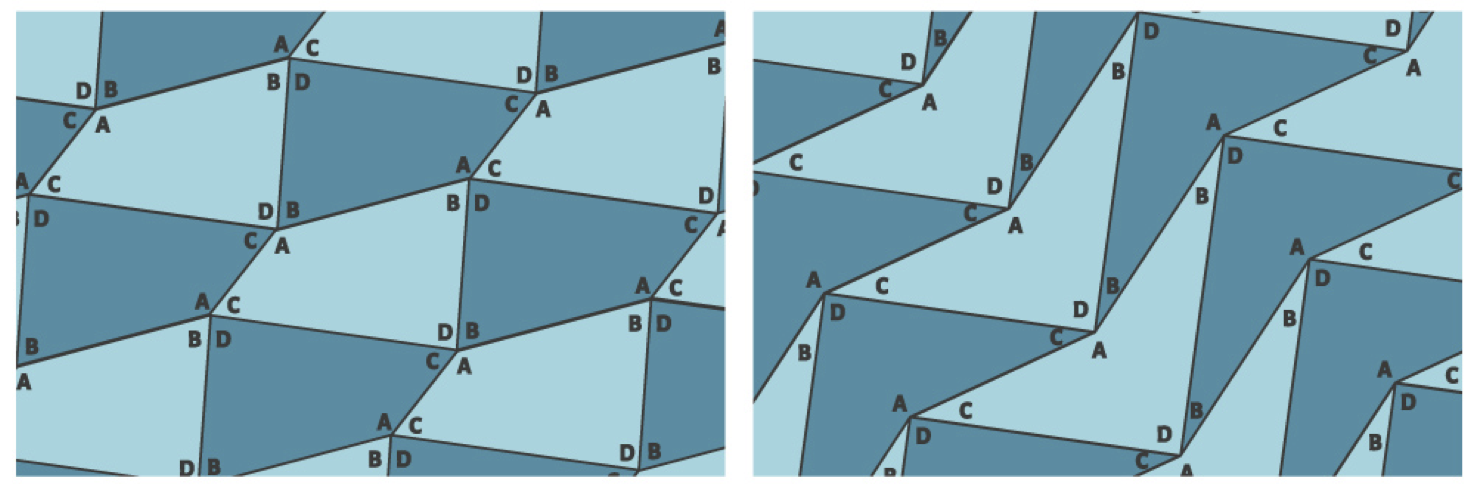
Históricamente, el tratamiento del problema de los hexágonos convexos que embaldosan el plano precedió al de los pentágonos. Para los primeros, todas las diferentes posibilidades fueron descritas por Karl Reinhardt en su tesis doctoral de 1918, realizada bajo la dirección del Ludwig Bieberbach y de cuya comisión examinadora formó parte nada menos que David Hilbert. Lamentablemente, este trabajo es muy extenso y complejo. De hecho, de acuerdo a uno de los especialistas del tema, Branko Grünbaum, “tanto la tesis de Reinhardt como trabajos posteriores en este tema específico son tremendamente complicados, y muy probablemente incompletos; sería muy útil retomarlos hasta obtener una simplificación que sea digerible” [1]B. Grünbaum. Comunicación personal.. Pese a esto, la comunidad concuerda en que ella es correcta.
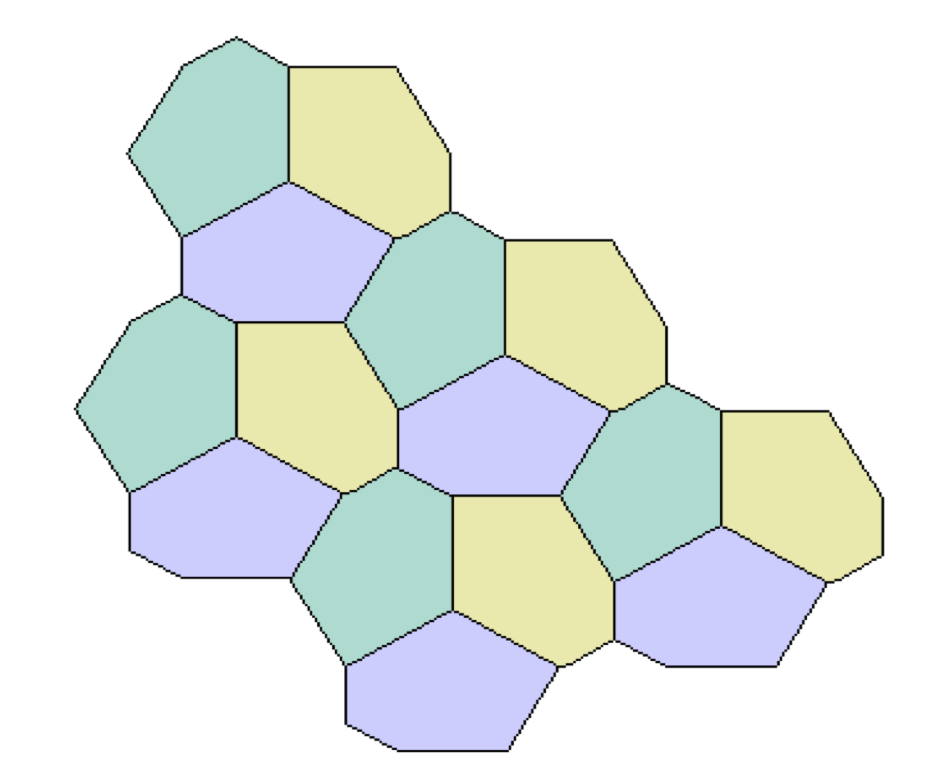
La historia del problema de determinar cuáles son los pentágonos convexos que embaldosan el plano, aún inconclusa, es de lo más insólito en la matemática reciente. Tras décadas de trabajo, la solución fue anunciada por Richard Kershner en 1968. Según él, habrían solo ocho tipos de pentágonos que logran cubrir el plano. Cabe señalar que no se trata de pentágonos en particular, sino más bien de grupos conformados por pentágonos con características particulares comunes. Por ejemplo, el plano es cubierto por todo pentágono de lados a, b, c, d, e y ángulos A, B, C, D, E en el que b y c tengan la misma longitud, d y e midan lo mismo, y B y D sean ángulos rectos. Esta familia corresponde a la cuarta de las ilustradas más abajo, y a ella pertenece el embaldosado presentado a continuación y que decora algunas calles de la ciudad de El Cairo.

La argumentación de Kershner era muy elaborada. Por ello, inicialmente, solo se publicó una nota informativa del resultado en la revista American Mathematical Monthly. Su contenido fue comentado por Martin Gardner en su columna Mathematical Games de la revista Scientific American Magazine en 1975. Esta última llegó a las manos del experto en informática Richard James, quien hizo una lectura aguda de ella y... ¡descubrió un embaldosado pentagonal que no estaba en la lista de Kershner!
El resultado anunciado se revelaba entonces incorrecto. Pero la historia daría para mucho más. La nota de Gardner llegó también a las manos de Marjorie Rice, quien no tenía ningún tipo de formación científica, pero sí una curiosidad colosal. Las llamativas ilustraciones de la revista (dirigida por correo a su hijo) llamaron poderosamente su atención, inspirándola y motivándola a trabajar para entender lo propuesto allí. Recurriendo solo a los vagos recuerdos de sus lecciones de geometría del liceo, desarrolló técnicas y notaciones especiales para tratar el problema. El resultado fue espectacular: entre 1976 y 1977, logró descubrir nada menos que otros cuatro grupos de pentágonos que no estaban en la lista de Kershner. Con esto, íbamos ya en 13 familias pentagonales. Referimos al excelente artículo panorámico [7]D. Schattschneider. Tiling the plane with congruent pentagons. Math. Magazine 51 (1978), 29-44. para el estado del arte en torno al tema hasta 1978.
Algunos años más tarde, en 1985, Rolf Stein dio con un embaldosado pentagonal más [8]D. Schattschneider. A new pentagon tiler. Math. Magazine 58 (1985), 308.. La particularidad del pentágono asociado es que no pertenece a una familia grande, sino que tiene medidas angulares muy precisas (A=90°, B~145.34°, C~69.32°, D~124.66°, E~110.68°). Hasta ese instante, la lista quedaba en 14 tipos de pentágonos. El problema quedaría prácticamente enterrado y sin ningún avance por mucho tiempo.

Hubo que esperar 30 años para que un nuevo pentágono aflorara. Usando un algoritmo computacional, el equipo formado por Case Mann, Jennifer McLoud y David von Derau logró dar, en 2015, con un decimoquinto embaldosado pentagonal, ilustrado al final del cuadro más arriba y reproducido en detalle a continuación.

Nuevamente se trata de un pentágono muy preciso y sorprendentemente sencillo. De hecho, tal como se observa más abajo, ni las medidas de sus ángulos ni las proporciones entre las longitudes de sus lados son extraordinariamente exóticas. ¡Este pentágono hubiese podido perfectamente ser descubierto décadas antes!
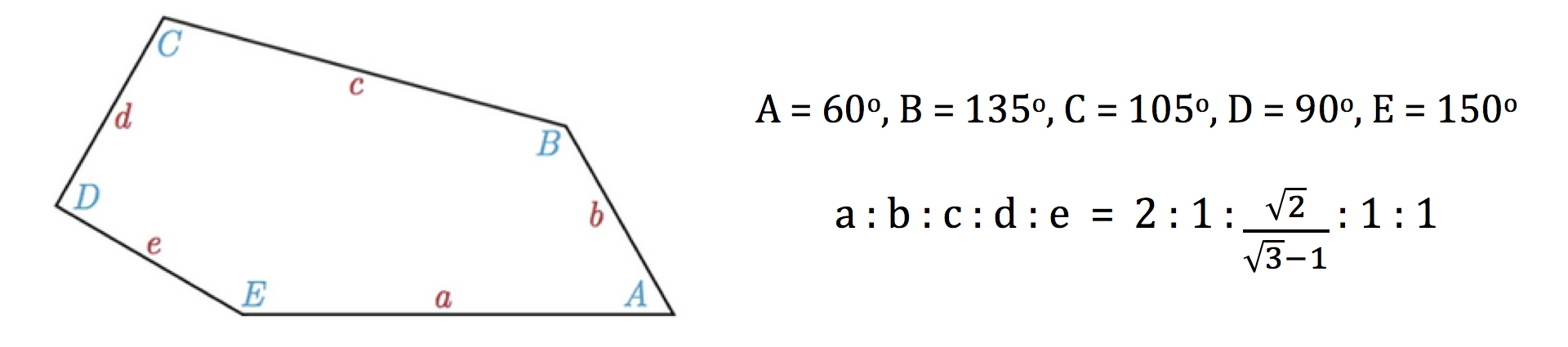
Pero este descubrimiento no cierra en absoluto el problema. Por el contrario, lo vuelve aún más interesante. ¿Se podrá agregar aún otro pentágono a la lista? ¿Se podrán agregar infinitos? Tan difícil es adivinar la respuesta como arriesgado es aventurar una conjetura al respecto.
Una curiosidad de los embaldosados exhibidos es su periodicidad. A priori, solo se indaga sobre la posibilidad de cubrir el plano, pero a posteriori se constata, en los ejemplos conocidos, que todos los pentágonos que lo consiguen también lo hacen en configuraciones que se trasladan en sí mismas en dos direcciones independientes. Más precisamente, si bien pueden embaldosar sin periodicidad (como queda ilustrado abajo a derecha, en una configuración descubierta por Michael Hirschhorn), también lo logran de forma periódica. ¿Es esto siempre así?, ¿o existirá un pentágono convexo que embaldose el plano pero nunca lo haga con periodicidad? Este problema es parte de uno aún mayor que involucra polígonos en general, ya sean convexos o no. Con esta generalidad, es conocido como el “problema Einstein”, nombre que no tiene ninguna relación con el célebre físico y matemático, sino que nace de un simple juego de palabras del alemán: ein (uno) y stein (ladrillo). Se trata, sin duda alguna, de otro acertijo intimidante, casi un reto pugilístico para quien se atreva a lidiar con él.
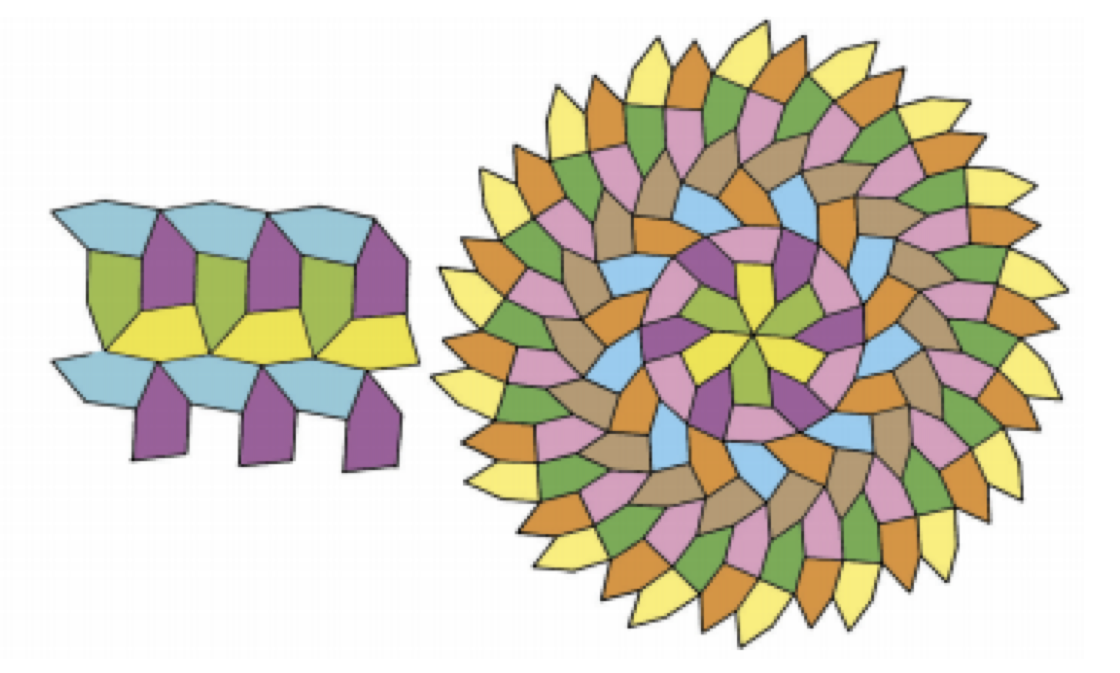
En décadas recientes, el estudio de los polígonos que embaldosan el plano sin periodicidad ha cobrado un enorme interés debido a una razón proveniente desde fuera de la matemática. En efecto, el año 2011, Dan Shechtman fue galardonado con el Premio Nobel de Química por un descubrimiento realizado décadas antes: la mañana del 8 de Abril de 1982, con la ayuda de un microscopio electrónico, observó por primera vez un cristal “exótico”. El trabajo resultante tardó un par de años en ser publicado, pues la comunidad científica se resistió inicialmente a validar su contenido. ¿La razón? Shechtman había echado por tierra una antigua ley de la cristalografía, según la cual los átomos de todos los cristales debiesen configuranse espacialmente siguiendo patrones que se repiten bajo traslaciones. La aleación metálica que sintetizó y observó en colaboración con su equipo de trabajo no cumplía con este precepto, por lo cual fue llamada un “cuasicristal”.
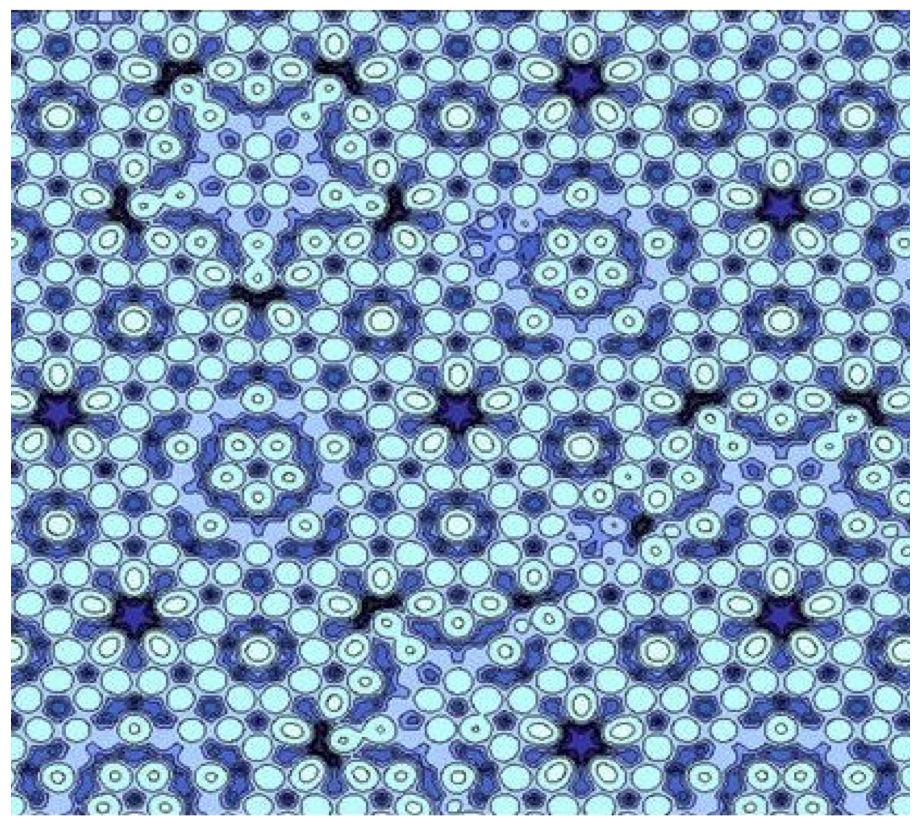
Una imagen obtenida por difracción a partir de uno de estos cuasicristales aparece ilustrada más abajo. Observando con atención, notará que la imagen no se copia a sí misma bajo ninguna traslación. Sin embargo, sus motivos sí se repiten infinitas veces de manera cuasiperiódica. Más precisamente, cualquier configuración finita aparecerá en toda parte de la configuración global que tenga un tamaño apropiado.
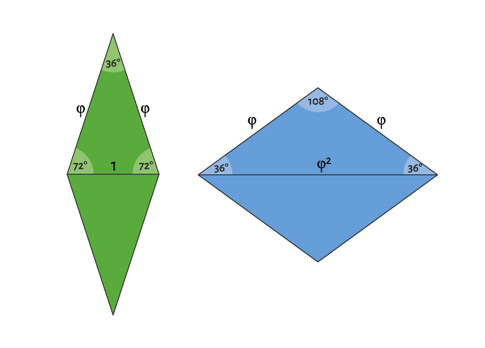
Las estructuras geométricas abstractas que verifican esta propiedad eran conocidas en matemática desde antes del descubrimiento de Shechtman. En particular, tras el trabajo pionero de 1961 del especialista en lógica Hao Wang, cinco años más tarde, Robert Berger descubrió una familia de 20.426 polígonos que no logran cubrir el plano con repetición traslacional, pero sí lo hacen cuasiperiódicamente. Esta construcción fue brillantemente simplificada por el célebre físico y matemático Roger Penrose, quien, entre 1973 y 1974, construyó embaldosados con las mismas propiedades usando tan solo dos piezas. En uno de ellos, el embaldosado rómbico ilustrado más abajo, una de las piezas nace de dos triángulos de ángulos 36°, 72° y 72° (los “triángulos áureos”) pegados a lo largo del lado menor, mientras que la otra nace de dos triángulos de ángulos 36°, 36° y 108° (los “gnomons áureos”) pegados a lo largo del lado mayor. Estas figuras están escaladas adecuadamente para que sus lados midan exactamente lo mismo, de modo que puedan acoplarse unas con otras.
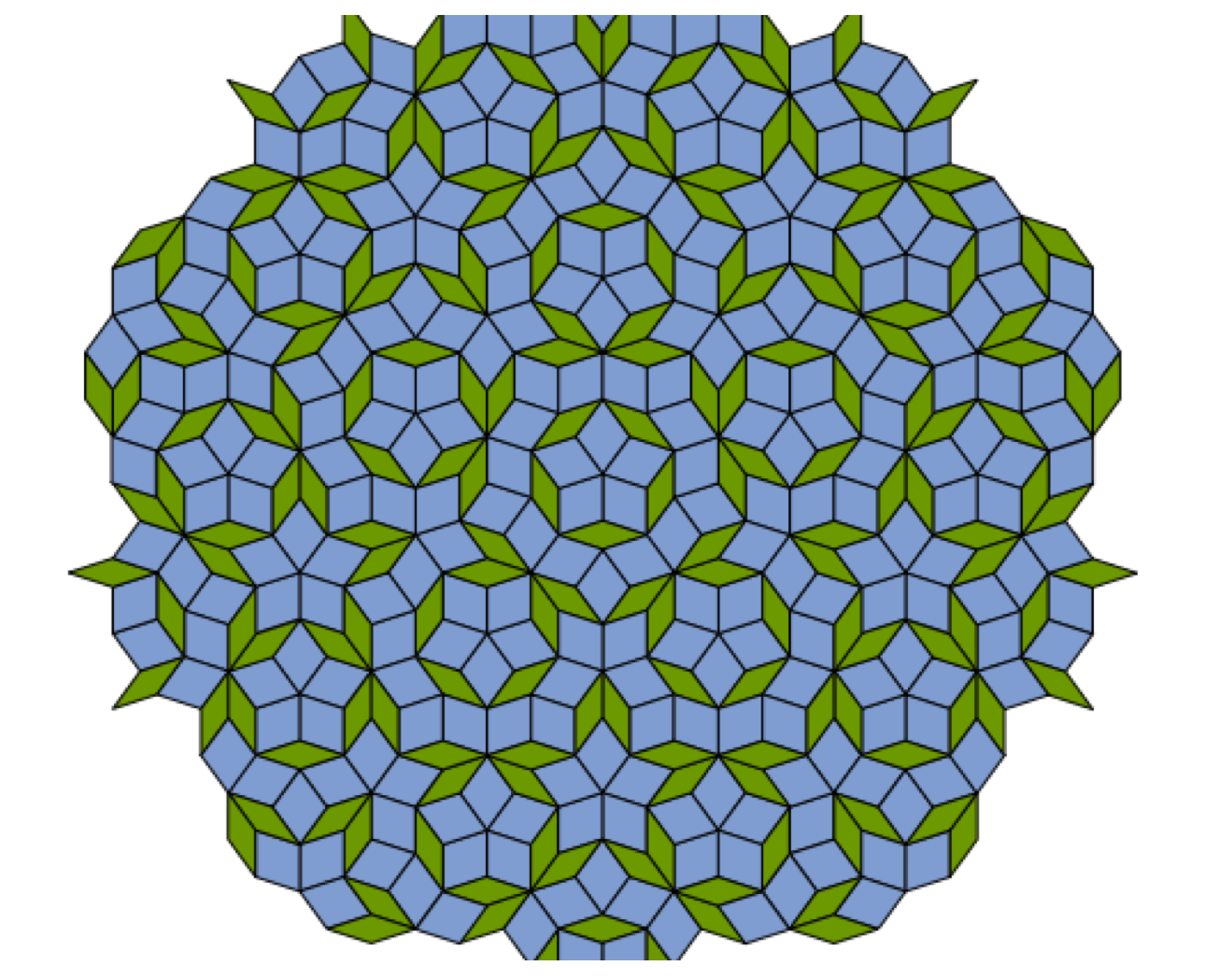
Embaldosado de Penrose: configuración cuasiperiódica formada por dos piezas (recuerde que se ignora si existe una única pieza poligonal que cubra cuasiperiódicamente el plano pero no lo haga con simetrías de traslación).
Es muy importante señalar, sin embargo, que los rombos no se ensamblan de manera arbitraria, sino que existen reglas muy precisas para proceder. De hecho, con ellos se puede fabricar también embaldosados periódicos, como se muestra en la configuración a continuación, la cual era conocida desde tiempos antiguos y aparece, por ejemplo, en el diseño de la bandera de la Independencia de Chile [5]A. Navas. The amazing story of a forgotten golden flag. Prepublicación..
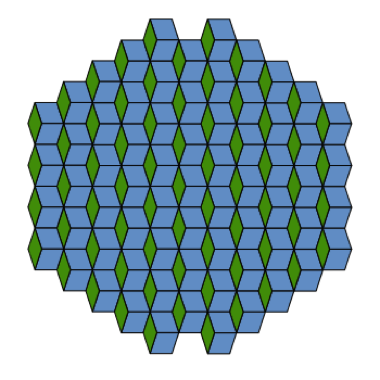
Así, en estricto rigor, las piezas usadas por Penrose son pequeñas variaciones de los rombos que reflejan estas reglas de ensamblaje. A menudo, esto se logra por modificaciones a lo largo de los lados mediante cuñas y hendiduras.
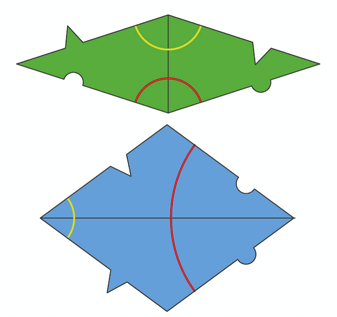
Una variación de la construcción precedente se logra usando dos piezas diferentes, apodadas el dardo y el volantín debido a su apariencia, las que son nuevamente formadas por pares de gnomons y triángulos áureos, esta vez pegados de manera diferente.
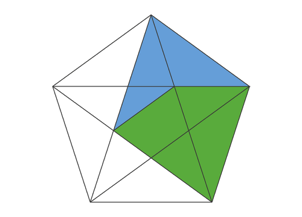
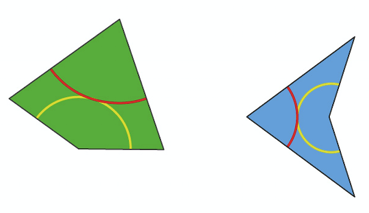
Construcciones concretas de embaldosados de Penrose usando estas piezas pueden ser obtenidas mediante un proceso de subdivisión esquematizado en el cuadro presentado a continuación, el cual es autoexplicativo. Los embaldosados son, por lo tanto, autosimilares, lo cual tiene una consecuencia notable sobre su geometría a gran escala: para cada uno de ellos, existe un homeomorfismo bilipschitziano del plano que envía sus vértices sobre el conjunto de los puntos de coordenadas enteras [4]A. Navas. Une remarque à propos de l’équivalence bilipschitzienne entre des ensembles de Delone. (A remark concerning bi-Lipschitz equivalence of Delone sets.) Prepublicación.. Cabe señalar que existen embaldosados cuasiperiódicos por polígonos del plano cuyo conjunto de vértices no puede ser enviado sobre el conjunto de puntos de coordenadas enteras de manera bilipschitziana [2]M. Cortez & A. Navas. Some examples of repetitive, non-rectifiable Delone sets. Geometry & Topology (por aparecer)..
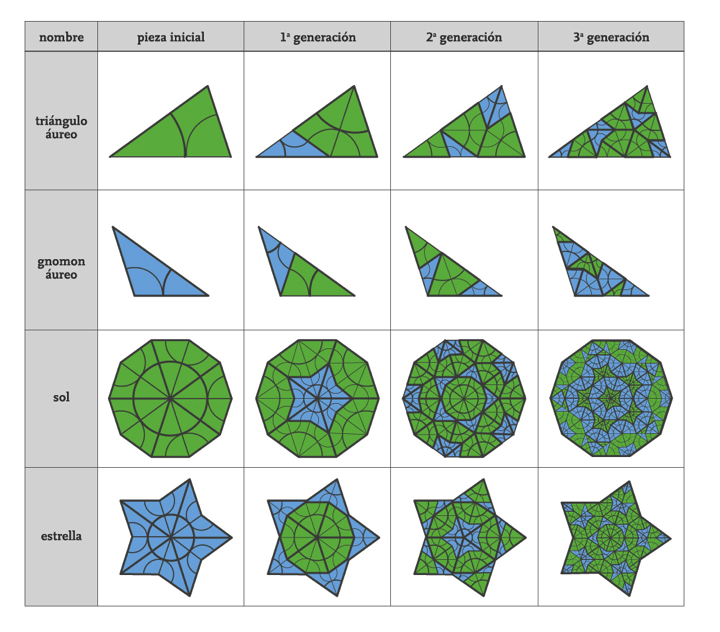
Ciertamente, las piezas usadas por Penrose están muy relacionadas con la geometría pentagonal y, por consiguiente, con la razón áurea. De hecho, en cada una de las configuraciones globales, la razón entre la cantidad de piezas que aparecen con mayor y menor proporción debiese ser cada vez más parecida al número de oro φ si se contabiliza a lo largo de regiones más y más grandes. Esto muestra, en particular, que no puede haber simetría traslacional, pues si la hubiese, entonces dicha razón debiese aproximarse cada vez más a un número racional. Además, esto explica otra característica muy especial de los embaldosados de Penrose ilustrados arriba, presente también en la imagen del cuasicristal ilustrado anteriormente: la existencia de una simetría rotacional de orden 5. Este aspecto no es menor pues, de acuerdo a una ley llamada “restricción cristalográfica” (cuya demostración —sencilla— dejamos a cargo del lector), si una configuración que cubre el plano se repite traslacionalmente en alguna dirección, entonces solo puede tener simetrías rotacionales de orden 2, 3, 4 o 6. De este modo, las rotaciones de orden 5 están prohibidas para los cristales, pero autorizadas para los cuasicristales.
Hasta el día de hoy no se ha encontrado ningún cuasicristal sobre la faz de la Tierra y oriundo de ella. Sin embargo, dichas estructuras existen en el universo de manera natural, tal como lo revelaron los restos descubiertos en 2012 de un asteroide caído en las montañas de Koryak en Siberia [10]N.T. Redd, Strange Crystals Reveal Rock to be Ancient Meteorite, Space.com, 03.01.12.. De alguna manera, condiciones similares a las del laboratorio de Shechtman son (o, al menos, fueron) replicadas en alguna región del espacio exterior.
De la misma forma que la propia naturaleza había anticipado el trabajo de Shechtman, la invención de Penrose había sido precedida por la sabiduría de tiempos ancestrales. Así lo reveló el trabajo del año 2007 del entonces estudiante Peter J. Lu en conjunto con el físico Paul Steindhardt [3]P. Lu & P. Steinhardt. Decagonal and quasi-crystalline tilings in medieval islamic architecture. Science 315 (2007), 1106-1110., quienes constataron que en ciertos periodos de la cultura islámica fueron elaboradas en Persia —actual Irán— configuraciones que cumplen las propiedades de cuasiperiodicidad y no repetitividad por traslaciones. Sin duda alguna, el ejemplo más espectacular corresponde al templo Darb-i Iman, ubicado en la ciudad de Isfaham y construido (y decorado) en 1453.

¿Quiénes deben ser considerados entonces los verdaderos descubridores/inventores de los cuasicristales y de los embaldosados cuasiperiódicos? Esta pregunta apunta ciertamente a algo más profundo, a saber, si los procesos naturales y la matemática misma nos preceden o son meras conceptualizaciones humanas. Difícil discusión, en la que no pretendemos entrar acá.
De manera más terrenal, podemos preguntarnos también a quién “pertenecen” estas estructuras. Paradójicamente, el mismo Penrose se vio envuelto en una insólita discusión al respecto. En 1995, ante el otorgamiento de una patente comercial al experto en computación Roger Schlafly por el descubrimiento de dos nuevos números primos y sus eventuales aplicaciones prácticas, había reaccionado molesto señalando que “la matemática existe para todos”. Sin embargo, distinta fue su reacción cuando en 1997 llegó a sus manos un rollo de papel tisú Kleenex, cuyo diseño replicaba uno de sus embaldosados. Supuestamente, esto lo hacía más llamativo pues evitaba que los pliegues del papel mullido se superpusieran uno sobre otro de manera repetitiva, creando una impresión ligeramente desagradable a la vista y al tacto. Lamentablemente, se produjo una disputa por propiedad intelectual que escaló hasta la corte de justicia, en la que se enfrentaron Penrose y su propia firma, Pentaplex Limited, contra la empresa Kimberly Clark Limited, que había tomado el control de la producción del papel Kleenex [11]Kleenex art that ended in tears, Independent, 11.04.97.. Afortunadamente, al final primó la cordura, y ambas partes llegaron a un acuerdo de colaboración. Gracias a esto, podremos seguir disfrutando de minutos placenteros contemplando la no repetitividad de un bello papel tisú...

[1] B. Grünbaum. Comunicación personal.
[2] M. Cortez & A. Navas. Some examples of repetitive, non-rectifiable Delone sets. Geometry & Topology (por aparecer).
[3] P. Lu & P. Steinhardt. Decagonal and quasi-crystalline tilings in medieval islamic architecture. Science 315 (2007), 1106-1110.
[4] A. Navas. Une remarque à propos de l’équivalence bilipschitzienne entre des ensembles de Delone. (A remark concerning bi-Lipschitz equivalence of Delone sets.) Prepublicación.
[5] A. Navas. The amazing story of a forgotten golden flag. Prepublicación.
[6] I. Niven. Convex polygons that cannot tile the plane. American Math. Monthly 54 (1978), 785-792.
[7] D. Schattschneider. Tiling the plane with congruent pentagons. Math. Magazine 51 (1978), 29-44.
[8] D. Schattschneider. A new pentagon tiler. Math. Magazine 58 (1985), 308.
[9] Euclidean tilings by convex regular polygons, artículo de Wikipedia.
[10] N.T. Redd, Strange Crystals Reveal Rock to be Ancient Meteorite, Space.com, 03.01.12.
[11] Kleenex art that ended in tears, Independent, 11.04.97.
