

Continuamos nuestra serie de problemas de olimpiadas con una aplicación de la fórmula de Green, que se puede utilizar como un atractivo ejemplo en un curso de cálculo diferencial e integral. El problema que presentamos apareció hace muchos años en la revista rusa de matemáticas Квант (Kvant):
Este problema fue propuesto por M. Kontsevich (en aquel tiempo, alumno de preparatoria). La solución, publicada en la revista por N. Vassiliev e I. Klumova, es como sigue:
(a) El polígono tiene el mismo número de lados verticales que horizontales, porque los lados verticales y horizontales se suceden unos a otros. Entonces $n=2k$, donde $k$ es el número de lados verticales (horizontales).
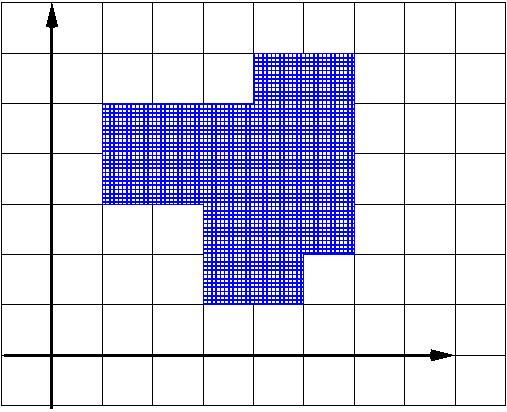
Introducimos un sistema de coordenadas con ejes coincidiendo con dos de las líneas del cuadriculado (Figura 1). Sean las coordenadas de los vértices consecutivos: \begin{eqnarray*} (a_1,b_1), (a_2,b_1),(a_2,b_2), (a_3,b_2),(a_3,b_3),\ldots, (a_{k-1},b_{k-1}), \\ (a_{k},b_{k-1}),(a_{k},b_{k}), (a_1,b_{k}). \end{eqnarray*} Sabemos que todos los números $a_{j+1}-a_j$, $b_{j+1}-b_j$ son enteros impares, $j=1,2,\ldots, k$ (donde $a_{2m+1}=a_1$, $b_{k+1}=b_1$). Como todas las diferencias $a_{j+1}-a_j$ son impares, las paridades de los números \begin{eqnarray*} a_1,a_2,\ldots, a_{k},a_{k+1}=a_1 \end{eqnarray*} alternan, y esto es posible sólo si $k$ es par, sea $k=2m$. Entonces, $n=2k=4m$ es un múltiplo de $4$. Esto demuestra (a).
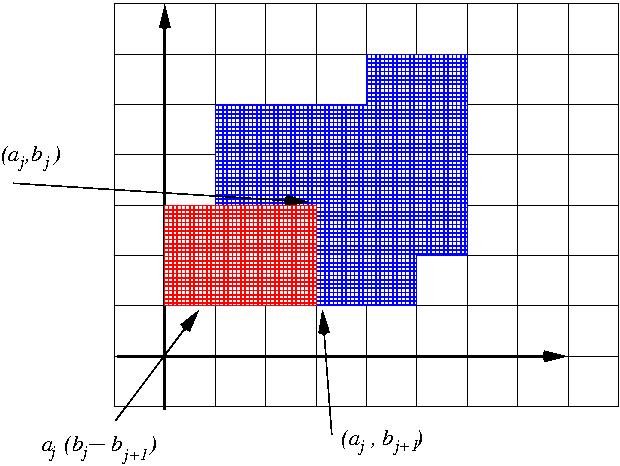
La segunda parte del problema es un poco más difícil, y es la parte que nos interesa. Representando el área del polígono como sumas y diferencias de las áreas de los rectángulos $|a_j(b_{j+1}-b_j)|$ (vea Figura 2), obtenemos la fórmula para el área: \begin{eqnarray}\label{greenformula} A=\left|\sum_{j=1}^{2m}a_j(b_{j+1}-b_j)\right|. \end{eqnarray}
Como todas las diferencias $b_{j+1}-b_j$ son impares, la suma tiene la misma paridad que $a_1+a_2+\cdots +a_{2m}$. Por otro lado, como las paridades de los números $a_1,a_2,\ldots, a_{2m}$ alternan, las sumas $a_1+a_2,a_3+a_4,\ldots, a_{2m-1}+a_{2m}$ son impares. Escribimos \begin{eqnarray*} a_1+a_2+a_3+\cdots +a_{2m}=(a_1+a_2)+(a_3+a_4)+\cdots +(a_{2m-1}+a_{2m}), \end{eqnarray*} que es una suma de $m$ números impares. Deducimos que esta suma tiene la misma paridad que $m$, y lo mismo se cumple para el área del polígono. Para $n=100$, $m=25$, y la suma es impar. Esto concluye (b).
Cuando este problema fue presentado en el programa estadounidense de entrenamiento para la Olimpiada Internacional de Matemática en 2010, varios alumnos reconocieron que (\ref{greenformula}) es la fórmula de Green para calcular el área de un dominio. Recordamos que la fórmula de Green para un campo vectorial
\begin{eqnarray*} \vec{F}(x,y)=(f(x,y),g(x,y))=f(x,y){\bf i}+g(x,y){\bf j} \end{eqnarray*} definido en el dominio $D$ del plano, con frontera $\gamma$ orientada hacia la izquierda como en la Figura 3, es \begin{eqnarray*} \iint_D\left(\frac{\partial g}{\partial x}-\frac{\partial f}{\partial y}\right)dxdy=\oint_\gamma (fdx+gdy) \end{eqnarray*}
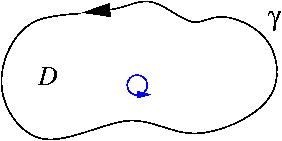
La integral a la derecha calcula la circulación del campo en la frontera, y el término \begin{eqnarray*} \frac{\partial g}{\partial x}-\frac{\partial f}{\partial y} \end{eqnarray*} que integramos sobre $D$ es la circulación infinitesimal $\mathrm{curl}\, \vec{F}$ en un punto. La fórmula de Green nos da la circulación en la frontera como la suma de las circulaciones infinitesimales en todos los puntos del dominio.
En el caso particular del campo vectorial $\vec{F}=(0,x)=x\bf{j}$ definido en la superficie del polígono obtenemos: \begin{eqnarray*} \iint_D1dxdy=\int_\gamma xdy, \end{eqnarray*} donde $\gamma$ es la frontera y $D$ es el interior del polígono. La integral en la parte izquierda es el área del polígono. La integral en la parte derecha es \begin{eqnarray*} \pm\sum_{j=1}^{2m}a_j(b_{j+1}-b_j) \end{eqnarray*} con el signo positivo, si el polígono es orientado hacia la izquierda, y negativo, si es orientado a la derecha. Así, obtenemos (1) como un caso particular de la fórmula de Green.
