En este artículo discutimos la aplicación de la desigualdad isoperimétrica en un problema que apareció en el examen de selección del equipo que representó a Rumania en la Olimpiada Internacional de Matemática en 2005.
Empezamos con una solución elemental basada en la idea del alumno Alin Purcaru:
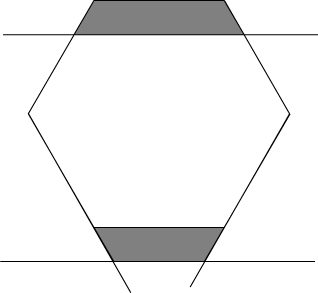
Sea $K$ el polígono. Dado que cada banda con el ancho igual a 1 se puede trasladar paralelamente de manera que cubre $K$, podemos colocar $K$ en la intersección de tres bandas con anchos iguales a 1 que forman ángulos de $\frac{2\pi}{3}$. Esta intersección es un hexágono con ángulos iguales cuyos lados opuestos están a la distancia 1.
Demostraremos que
Estas propiedades son fáciles de demostrar en el caso de un hexágono regular. Para el caso general, observemos que la interseccion de dos de las bandas siempre es el mismo paralelogramo con una altura igual a 1 y con un ángulo de $\frac{\pi}{3}$ y, entonces, la forma del hexágono depende solamente de la posición de la tercera banda.
Debido a esto, podemos obtener el hexágono por una traslación de un par de lados opuestos del hexágono regular de manera que la distancia entre ellos sigue siendo 1. Observamos que, en el proceso, perdemos un trapecio y ganamos un trapecio (Figura 1). Los dos trapecios tienen los mismos ángulos y la misma altura, pero las bases del trapecio que perdemos son mayores que las bases del trapecio que ganamos. Por tanto, el área disminuye y esto demuestra (i).
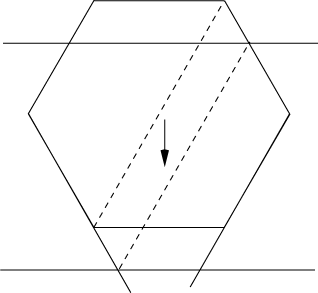
Ademas, en el proceso de traslación, las direcciones de las tres diagonales entre los vértices opuestos del hexágono no se cambian; las diagonales simplemente se trasladan (Figura 2). Esto demuestra (ii).
Para concluir la solución observamos que (i) implica que el área de $K$ es igual o menor a $\frac{\sqrt{3}}{2}$. Sin embargo, (ii) implica que $K$ no puede coincidir con la intersección de las tres bandas (ya que $\frac{2}{\sqrt{3}}>1$) y, entonces, la desigualdad de los áreas es estricta.
Existe otra solución (basada en una idea de Gabriel Kreindler), la cual utiliza la desigualdad isoperimétrica. Antes que todo explicamos el significado de esta desigualdad. ¿Qué es lo que dice en realidad?
Demostración (Hurwitz). Consideremos una parametrización $\gamma=(x(t),y(t)):[0, 2\pi]\to\mathbb{R}^2$ de la curva $\Gamma$ con velocidad constante $\displaystyle |\gamma^{\prime}(t)|=\frac{L}{2\pi}$, $t\in [0, 2\pi]$. Las funciones $x$ y $y$ se pueden extender periódicamente en $\mathbb{R}$. Ahora, podemos escribir las funciones $x:[0, 2\pi]\to\mathbb{R}$ y $y:[0, 2\pi]\to\mathbb{R}$ utilizando las series de Fourier: $$\displaystyle x(t)=\sum_{n\in\mathbb{Z}}a_{n}e^{int} \mbox{ y }\displaystyle y(t)=\sum_{n\in\mathbb{Z}}b_{n}e^{int}.$$ Tenemos que: $$\displaystyle x^{\prime}(t)=\sum_{n\in\mathbb{Z}}ina_{n}e^{int} \mbox{ y } \displaystyle y^{\prime}(t)=\sum_{n\in\mathbb{Z}}inb_{n}e^{int}.$$
Una aplicación de la identidad de Parseval dará la relación: $$\displaystyle\frac{L^2}{2\pi}=\int_0^{2\pi}(x^{\prime}(t))^2+(y^{\prime}(t))^2dt=2\pi\sum_{n\in\mathbb{Z}}n^2(|a_{n}|^2+|b_{n}|^2).$$ Por otra parte, de la fórmula de Green obtenemos $$\displaystyle A=\frac{1}{2}\left|\int_0^{2\pi}(x(t)y^{\prime}(t)-x^{\prime}(t)y(t)))dt\right| = \pi\left|\sum_{n\in\mathbb{Z}}n(a_{n}\overline{b_{n}}-\overline{a_{n}}b_{n})\right|.$$ Entonces, $$\displaystyle 4\pi A=4\pi^2\left|\sum_{n\in\mathbb{Z}}n((a_{n}\overline{b_{n}}-\overline{a_{n}}b_{n})\right|\leq 4\pi^2\sum_{n\in\mathbb{Z}}|n||a_{n}\overline{b_{n}}-b_{n}\overline{a_{n}}|\leq$$ $$\displaystyle\leq 4\pi^2\sum_{n\in\mathbb{Z}}|n|(|a_{n}|^2+|b_{n}|^2)\leq4\pi^2\sum_{n\in\mathbb{Z}}n^2(|a_{n}|^2+|b_{n}|^2)=L^2,$$ ya que $$\displaystyle |a_{n}\overline{b_{n}}-\overline{a_{n}}b_{n}|\leq 2|a_{n}||b_{n}|\leq |a_{n}|^2+|b_{n}|^2.$$
La igualdad se obtiene si $a_{n}=b_{n}=0$ para $n\geq 2$, lo que implica $\displaystyle |a_{n}|=|b_{n}|$ para $n=1$. Esto significa que la igualidad se tiene cuando $\gamma$ es una circumferencia.
Regresemos a nuestro problema.
Para una recta $\ell$ arbitraria con el ángulo polar $\theta$, denotemos $r(\theta)$ la longitud de la proyección del polígono $K$ en la recta $\ell$. Entonces, el perímetro del polígono $K$ se puede expresar con la fórmula: $$\displaystyle P=\int_0^{\pi}r(\theta)d\theta, \quad r(\theta)\leq 1.$$
Obviamente, $\displaystyle P\leq \pi$; utilizando la desigualdad isoperimétrica, obtenemos que el área $A$ de $K$ es menor que $\displaystyle\frac{\pi}{4}<\frac{\sqrt{3}}{2}$. $\square$
Para más información sobre la desigualdad isoperimétrica, el lector puede consultar el artículo [1].
[1] V. Blåsjö, The evolution of the isoperimetric problem, Amer. Math. Monthly, 221 (2005), 526-566.
