Un camino simple a los finales primos

La frontera de una región simplemente conexa (= sin agujeros) en el plano puede ser extremadamente complicada. Es un ejemplo de un continuo (= compacto + conexo) planar y es posible que separe el plano en una infinidad de componentes complementarias. Es posible que admita ser cortada en dos por cualquiera de una infinidad de sus propios puntos. No necesita ser localmente conexa. Aunque los conjuntos “fractales” — ejemplo típico del conjunto cerrado patológico — han recibido mucha atención, tanto en la investigación como en la divulgación al público general, la estructura de los continuos planos todavía no se comprende cabalmente.

El renombrado teorema de Riemann de transformación conforme (“Riemann Mapping Theorem”) nos dice que, sin importar la complejidad de las fronteras de dos regiones simplemente conexas $D$, $D'$ en el plano (distintas del plano mismo; hipótesis que siempre mantendremos pero sin repetirla), existe una función analítica $f$ que es un homeomorfismo de $D$ sobre $D'$ (un homemorfismo analítico se llama también una transformación conforme). A menudo, en el trabajo del análisis complejo, es necesario saber cuándo una función $f$ puede extenderse en alguna forma razonable a la frontera de $D$, y en aquellos casos cuando no se puede, por lo menos, saber algo sobre los posibles valores límite de $f(z)$ cuando el punto $z$ tiende desde dentro de $D$ a algún punto frontera.

La solución completa a este problema para las transformaciones conformes fue dada hace más de un siglo por Constantin Carathéodory [6]Carathéodory, C. Über die Begrenzung einfach zusammenhängender Gebiete, Math. Ann. 73, 323-370 (1913). quien introdujo el concepto de “finales primos” (“prime ends”, en inglés, que se han expresado en español también como “extremos primos” o “puntas primas”, entre otros), una noción abstracta que describe un acercamiento a la frontera de la región. Carathéodory mostró hace 102 años que la función de Riemann determina una correspondencia 1-a-1 entre los finales primos de $D$ y los de $D'$. La idea no solamente es tremendamente elegante: sus consecuencias son sumamente prácticas. Cuando las fronteras $\partial D$, $\partial D'$ son lo suficientemente sencillas, podemos interpretar los finales primos geométricamente en términos de los verdaderos puntos frontera, y así deducir algo sobre el comportamiento de $f$ en la frontera. Por ejemplo, veremos que cuando las fronteras son curvas de Jordan (= simples y cerradas), los finales primos se reducen a puntos y la conclusión es que $f$ se extiende a un homeomorfismo de las regiones. Si estas curvas satisfacen condiciones adicionales de diferenciabilidad, tales condiciones se transmiten a la restricción de $f$ a la frontera también.

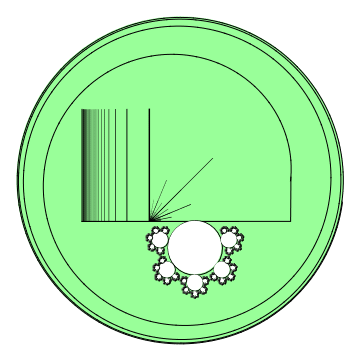
Este tema es ya muy clásico y se ha tratado en numerosos textos del análisis complejo, de los cuales algunos de los más famosos están en la bibliografía. En mi opinión, la presentación en muchos de estos textos deja algo que desear. Tienden a incluir una serie de lemas bastante especializados sobre funciones analíticas, intercalados con consideraciones sobre la topología del plano. Peor aún, en algunas de estas presentaciones, la definición misma de final primo hace uso de la transformación de Riemann del disco unitario a $D$, y esto da una impresión equivocada de que un final primo no es algo intrínseco a $D$ como subconjunto del plano. Tal enfoque disminuye la fuerza del teorema de Carathéodory. Muchos textos de variable compleja (quizás la mayoría) hacen que el tema parezca aún más abrumador simplemente porque dejan el teorema en su completa generalidad como “más allá del alcance del presente texto” y, de hecho, siguen apareciendo artículos y tesis que tratan alguna simplificación de la demostración para casos particulares (sobre todo para las curvas de Jordan).

Una demostración del teorema de Carathéodory que goza de gran belleza y no sufre de ninguno de los defectos mencionados fue dada por Jacqueline Lelong-Ferrand [13]Lelong-Ferrand, J. Representation conforme et transformations intégrale de dirichlet bournée. (francés) Gauthier-Villars, Paris, 1955. quien logró colocar todo el análisis complejo en una sola desigualdad (válida, mencionamos de paso, para una clase de maps mucho más generales que los analíticos — las transformaciones casiconformes). El resto del desarrollo del tema es, entonces, puramente topológico, y cada paso de la demostración para regiones de complejidad arbitraria puede entenderse de forma muy intuitiva para los casos cuando la frontera no sea demasiado patológica. Puesto que su enfoque parece no ser muy bien conocido ni de fácil acceso y, en conmemoración del fallecimiento de la profesora Lelong-Ferrand el año pasado (por cierto, ella nació a los cinco años de la publicación de [6]Carathéodory, C. Über die Begrenzung einfach zusammenhängender Gebiete, Math. Ann. 73, 323-370 (1913).), presentamos sus ideas aquí en una formulación que fácilmente podrá adaptarse a una presentación en aula de clase. Incluimos al final una sección corta que muestra cómo se pueden deducir, como consecuencias del Teorema de Carathéodory, los hechos básicos sobre la comportamiento de $f$ en la frontera, incluido el teorema de extensión para los dominios de Jordan y el teorema de Schoenfliess siguiendo la lógica del desarrollo en [9]Goluzin, G. M. Geometric theory of functions of a complex variable. Translations of Mathemaical Monographs, Vol. 26, American Mathematical Society, Providence, R.I., 1969., [13]Lelong-Ferrand, J. Representation conforme et transformations intégrale de dirichlet bournée. (francés) Gauthier-Villars, Paris, 1955., [14]Markushevich, A. I. Theory of functions of a complex variable., Vol. III. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1967., [21]Tsuji, M. Potential theory in modern function theory. Reimpresión de la edición de 1959. Chelsea Publishing Co., New York, 1975. y, sobre todo, la excelente presentación de [18]Pommerenke, C. Univalent Functions. Vandenhoeck & Ruprecht, Göttingen, 1975..

En la bibliografía, me he tomado la libertad de expresar unas opiniones propias sobre el trato que el tema ha recibido en diversas referencias.

1. Notación y enunciado

Para nosotros $\Delta=\{z\in{\mathbb{C}}\colon\ |z|< 1\}$ será el disco unitario en el plano complejo ${\mathbb{C}}$, mientras $D,D'\subseteq\mathbb{C}$ serán regiones (= abiertas y conexas) simplemente conexas arbitrarias en ${\mathbb{C}}$, salvo que, para simplificar los argumentos, siempre supondremos que son acotadas antes del comentario final.

Para curvas $\gamma,\delta,\dots$ abiertas (= sin sus dos puntos extremos), escribiremos $\overline{\gamma},\overline{\delta},\dots$ para indicar que sus extremos existen y están incluidos.

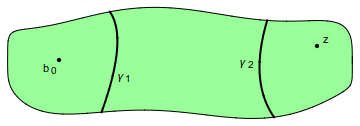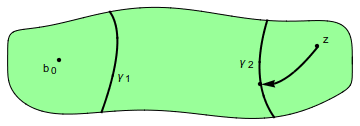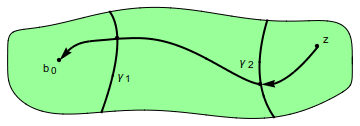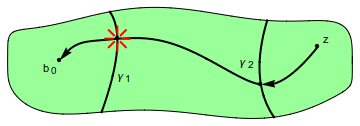
Un corte transversal de $D$ es una curva simple (= que no se autointersecta) $\gamma$ contenida en $D$ tal que los extremos de $\overline\gamma$ están en la frontera $\partial D$ de $D$. (No nos importa si los extremos coinciden.) Entonces el complemento $D\setminus\gamma$ es un abierto cortado por $\gamma$ en dos componentes conexas, cada una de las cuales es simplemente conexa, y $\gamma$ es la frontera relativa de cada una en $D$. Para calentar máquina, demostraremos esta afirmación: por el teorema de Riemann, $D$ es homeomorfo a $\Delta$, mientras $\Delta$ es homeomorfo a ${\mathbb{C}}$ (por $z\mapsto z/(1-|z|)$) y ${\mathbb{C}}$ puede encajarse topológicamente como subconjunto de una esfera $\widehat{{\mathbb{C}}}={\mathbb{C}}\cup\{\infty\}$, conocida como la esfera de Riemann, agregándole un sólo punto y definiendo la topología apropiada. En la esfera $\widehat{{\mathbb{C}}}$, podemos aplicar el teorema de Jordan (que afirma que una curva de Jordan divide la esfera en dos abiertos), pues bajo estas correspondencias $\overline{\gamma}$ es enviada precisamente a una curva de Jordan. Así obtenemos las dos componentes complementarias de $D$ que buscamos.

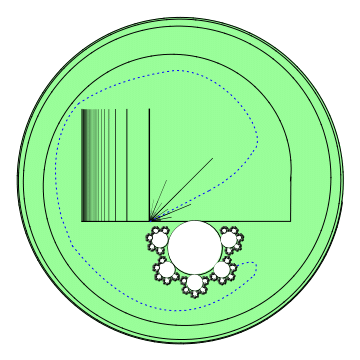
Fijaremos un “punto base” $b_0$ arbitrario en $D$. Cuando el corte transversal $\gamma$ no pasa por $b_0$, escribiremos $E(\gamma)$ para la componente conexa de $D\setminus\gamma$ que contiene a $b_0$, y $D(\gamma)$ para la otra componente. Es útil notar que para demostrar que algún punto $z\in D\setminus\gamma$ está en $E(\gamma)$, basta unirlo con $b_0$ con tan solo una curva en $D$ que no corte a $\gamma$. Por otra parte, para probar que $z$ está en $D(\gamma)$ tenemos que mostrar que toda curva que une $z$ a $b_0$ en $D$ se interseca con $\gamma$. Cuando el diámetro $|\gamma|$ es lo suficientemente pequeño (lo cual nos va a interesar), $\gamma$ no puede pasar por $b_0$ y así efectivamente los conjuntos $D(\gamma)$, $E(\gamma)$ están definidos.

Una de las metas de la teoría de los finales primos es introducir una “frontera ideal” para $D$ que sea invariante bajo las transformaciones conformes. Por ello queremos un concepto que pueda definirse, en lo posible, sin referencia a la frontera topológica o los puntos exteriores a $D$ en ${\mathbb{C}}$. Hay varias formas de definir estos “elementos de frontera”; aquí nos servirán los cortes transversales.

La definición de final primo es, de hecho, sencilla. Una sucesión $\gamma_1,\gamma_2,\dots$ de cortes transversales de $D$ se llama una cadena anidada cuando se satisfacen (a) $D(\gamma_{n+1})\subseteq D(\gamma_n)$ para todo $n$, y (b) $|\gamma_n|\to0$ cuando $n\to\infty$. Si, además, satisface (c) $\overline{\gamma}_{n+1}\cap\overline{\gamma}_n=\emptyset$ para todo $n$, es una cadena anidada propia (es un buen momento para observar que la condición (b) no implica que $|D(\gamma)|\to0$). Diremos que una cadena anidada $\{\gamma_n\}$ domina a otra $\{\gamma'_n\}$ si cada $D(\gamma_n)$ contiene algún $D(\gamma'_m)$. Si cada una de dos cadenas propias domina a la otra, diremos que son equivalentes, y la clase de equivalencia se llamará un final primo de $D$. Escribiremos $\widehat D$ para la unión de $D$ junto con sus finales primos, y $\partial\widehat D$ para el subconjunto de los puntos finales. Así $\widehat D=D\cup\partial\widehat D$. De la condición (b) podemos ver que la noción de punto final no depende de la elección del punto base $b_0$. El chiste de todo esto es que $\widehat D$ puede ser muy diferente de la clausura topológica $\overline{D}$. El lector que quiere ver de una vez la topología en $\widehat D$ puede pasar a a ese tema directamente.

El resultado de Carathéodory dice en esencia que las transformaciones conformes respetan los finales primos. En el enunciado, tomaremos el punto base en $D'$ como $b'_0=f(b_0)$.

Teorema de Carathéodory.

En la sección 4 daremos la demostración y mostraremos que, para el disco $\Delta$, se puede afirmar $\partial\widehat\Delta=\partial\Delta$ en un sentido natural, donde $\partial\Delta=\{z\colon\ |z|=1\}$. Entonces, el teorema de Carathéodory se interpreta en la siguiente forma equivalente (donde usamos $0\in\Delta$ como el punto base, y escribimos $\overline\Delta=\{z\colon\ |z|\le1\}$).

Teorema de Carathéodory.

En este enunciado no aparece ninguna mención explícita de la topología en $\widehat D$, pero la idea básica está incorporada.

2. Una desigualdad

Separamos la parte analítica de la topológica. Para la primera, no usaremos la teoría de la variable compleja más allá de las fórmulas para la longitud y el área de las imágenes de una curva y de una región bajo una función analítica. En esta sección no es necesario que la región $D$ sea simplemente conexa.

Proposición 1.

Demostración. Para el arco parametrizado $z=p+re^{i\theta}$, tenemos $|dz|=r\,d\theta$; así la longitud de $f(\delta_{r_,j})$ parametrizado por $w=f(p+re^{i\theta})$ es \[ \int_{\delta_{r,j}} |dw| = \int_{\theta_j}^{\theta'_j} r|f'(z)| \,d\theta. \] La desigualdad de Cauchy-Schwarz da \[ \lambda(r)^2 \le \int_{E_r} r^2\,d\theta \int_{E_r} |f'(z)|^2\,d\theta \le 2\pi r^2\int_{E_r} |f'(z)|^2\,d\theta, \] donde $E_r=\bigcup_j(\theta_j,\theta'_j)\subseteq[0,2\pi]$. Finalmente, \[ \int_R^{R'} \frac{\lambda(r)^2}{r}\,dr \le \int_R^{R'} \int_{E_r} |f'(z)|^2r\,dr\,d\theta \le A \] que es lo que necesitábamos (para justificarlo totalmente, se puede usar la hipótesis $A<\infty$ y el teorema de Fubini para ver que $ \int_{E_r} |f'(z)|^2 \,d\theta<\infty$ para casi todo $r$, luego $\lambda(r)<\infty$ para casi todo $r$).

▢

Corolario.

Demostración. Si esta afirmación fuera falsa, habría un radio $R'>0$ y un valor $b>0$ tales que $\lambda(r)>b$ cuando $0< r< R'$. Definimos $R=R'e^{-A/b^2}$, luego $R< R'$ y \[ \int_R^{R'} \frac{\lambda(r)^2}{r}\,dr > \int_R^{R'} \frac{b^2}{r}\,dr = b^2 \log\frac{R'}{R} = A, \] en contradicción a la Proposición 1.

▢

3. Topología en el plano

Ahora la parte topológica. No usaremos ninguna transformación conforme en los enunciados o demostraciones. El propósito es ver que cualquier final primo puede representarse por una cadena particularmente bonita (lema 7). Nuevamente, $D$ es simplemente conexa. Como en cualquier desarrollo de la variable compleja, el entendimiendiento se facilitará considerablemente cuando se hagan dibujos durante la lectura (lo hemos hecho para el primer lema).

Lema 1.

Demostración. Hay dos casos a considerarse. Si $\gamma_2\subseteq D(\gamma_1)$, entonces cualquier curva que una a cualquier $z\in D(\gamma_2)$ con $b_0$ en $D$ tendrá que cruzar $\gamma_2$, y luego seguir a cruzar $\gamma_1$ antes de llegar a $b_0$. Entonces, $z\in D(\gamma_1)$, lo cual nos dice que $D(\gamma_2)\subseteq D(\gamma_1)$. Nos queda considerar el caso $\gamma_2\subseteq E(\gamma_1)$. Podremos suponer que $\gamma_1\subset E(\gamma_2)$ también (de otro modo por el primer caso $D(\gamma_1)\subseteq D(\gamma_2)$). Ahora, para cualquier $z\in D(\gamma_1)$, podemos unir $z$ a un punto $z_1$ en $\gamma_1$ por una curva $\alpha_1\subseteq D(\gamma_1)$ (y así $\alpha_1$ no corta a $\gamma_2$), y luego unir $z_1$ a $b_0$ por $\alpha_2\subseteq E(\gamma_2)$. De esta manera $\alpha_1\cup\{z_1\}\cup\alpha_2$ une $z$ a $b_0$ sin cruzar a $\gamma_2$, luego $z\in E(\gamma_2)$. Por lo tanto, $D(\gamma_1)\subseteq E(\gamma_2)$, lo cual muestra que $D(\gamma_1)$, $D(\gamma_2)$ son disjuntos en este caso.

▢

Lema 2.

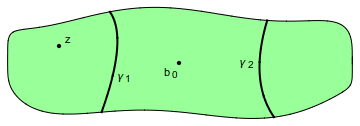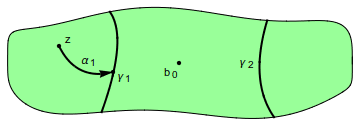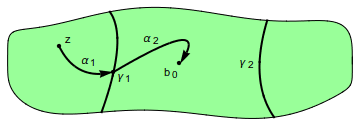
Demostración. Si $z\in D$ fuera un punto común de los $D(\gamma_n)$, uniríamos $z$ a $b_0$ por una curva $\alpha\subseteq D$, así $\alpha$ tendría que intersecar a cada $\gamma_n$. Como $|\gamma_n|\to0$, $\overline{\alpha}$ tendría que acumularse en alguna parte en $\partial D$, lo cual es una contradicción de $\overline{\alpha}\subseteq D$.

▢

Lema 3.

Demostración. Podemos suponer que $\{\gamma_n\}$ no domina a $\{\gamma'_n\}$. Tomemos $n$ tal que $D(\gamma_n)$ no contiene a ningún $D(\gamma'_m)$. Tomemos una subsucesión $\gamma'_{m_1},\gamma'_{m_2},\dots$ que converge a un punto $p\in\partial D$ (lo cual tiene sentido puesto que los diámetros tienden a 0). Reemplazando $n$ con $n+1$ en caso necesario (y recordando que las cadenas anidadas son propias), podemos suponer que $p$ no es un extremo de $\gamma_n$, de manera que para $j$ grande tenemos $\gamma'_{m_j}\cap\gamma_n\not=0$. Por el lema 2 es imposible que $D(\gamma_n)$ esté contenido en $D(\gamma'_{m_j})$ para todo $j$ grande; luego, por el lema 1, existe un $j$ para el cual son disjuntos, como se quería demostrar.

▢

Observemos que cuando $D(\gamma_n)$ y $D(\gamma'_m)$ son disjuntos para tan sólo un par de índices $m,n$, ningún de las cadenas puede dominar a la otra. Por lo tanto, tenemos lo siguiente.

Lema 4.

No podríamos llegar a la conclusión del lema 4 si una de las cadenas no fuera propia. Por ejemplo, sea $D=\{z\in\Delta\colon\ \mbox{Im}\, z>0\}$ el semicírculo superior. La cadena $\{z\in D\colon\ |z|=1/n\}$ domina a la cadena no propia $\{z\in D\colon\ |z-1/n|=1/n\}$, pero las dos no son equivalentes. Por eso la definición de final primo requiere cadenas propias.

Lema 5.

Demostración. Notemos que la clausura de $D_0$ relativo a $D$ está formada por $D_0$ con algunas de las $\delta_j$. Con $z$ como está descrito, unamos $z$ a $b_0$ por una curva poligonal finita $\alpha$ contenida en $D$. Entonces, $\overline{\alpha}$ corta a $C$ un número finito de veces, y procuremos tomar $\alpha$ para que este número sea mínimo.

Sea $\delta_j$ el primer arco de $C$ que es cruzado por $\alpha$ (pero no por $\overline{\alpha}$, considerando que posiblemente $z\in C$ y $z$ es extremo de $\alpha$.). Tal arco existe porque $z$ es exterior a $D_0$, mientras $b_0$ es interior. Dividamos a $\alpha$ como $\alpha=\alpha_1\cup\{z_0\}\cup\alpha_2$ donde $z_0\in\delta_j$ y $\alpha_1$ une $z$ con $z_0$. Las dos curvas $\alpha_1$, $\alpha_2$ no cortan a $\delta_j$, y $\alpha_2\subseteq E(\delta_j)$ porque finaliza en $b_0$. Si $z$ estuviera en $E(\delta_j)$, entonces también $\alpha_1\subseteq E(\delta_j)$, y se podría modificar $\alpha$ cerca de $z_0$ para formar una curva poligonal $\alpha'$ que no corta a $\delta_j$, así cortando a $C$ menos veces que $\alpha$. Esta contradicción muestra que $z\in D(\delta_j)$ y completa la demostración.

▢

Lema 6.

Demostración. Primero, establecemos que cada $D(\delta_j)$ está contenido en uno máximo. Pues, si fuera falso, habría una sucesión infinita $D(\delta_1)\subset D(\delta_2)\subset\cdots$ de inclusiones estrictas. Una curva fija $\alpha$ que una un punto $z\in D(\delta_1)$ a $b_0$ en $D$ cruzaría todas estas $\delta_j$ y, por lo tanto, se acumularía en un punto de $C\cap\partial D$, lo cual contradiría $\overline\alpha\subseteq D$.

En segundo lugar, notamos que si $z\in D(\gamma)$, entonces cualquier curva $\alpha\subseteq D$ de $z$ a $b_0$ toca a $\gamma$ y, por lo tanto, tiene que cruzar $C$. Como consecuencia, $z$ no puede estar en $\mbox{cerr}\,D_0$ en la notación del lema 5 y, por ese lema, tiene que estar en algún $D(\delta_j)$. Por lo tanto, $D(\gamma)\subseteq\bigcup_j D(\delta_j)$.

Finalmente, observamos que la unión de los $D(\delta_j)$ puede tomarse sobre los elementos máximos solamente. Así es una unión disjunta de conjuntos abiertos. Como $D(\gamma)$ es conexo, tiene que estar en un solo $D(\delta_j)$ máximo.

▢

Lema 7.

Demostración. Tomemos una subsucesión $\{\gamma_{n_m}\}$ de $\{\gamma_n\}$ que converge a $p\in\partial D$. Podemos suponer que $\gamma_{n_m}$ está dentro del círculo $C_m=\{|z-p|=r_m\}$. Para $m$ grande, $b_0$ está afuera. Descomponemos $C_m\cap D=\bigcup_j\delta_{m,j}$ como unión de sus subarcos conexos.

Por el lema 6, para cada $m$ podemos tomar $j$ tal que $D(\gamma_{n_m})$ está contenido en un dominio máximo $D(\delta_{m,j})$. Escribiremos $\gamma'_m=\delta_{m,j}$; entonces, \[ D(\gamma_{n_{m+1}}) \subseteq D(\gamma_{n_m}) \cap D(\gamma'_{m+1}) \subseteq D(\gamma'_m) \cap D(\gamma'_{m+1}), \] y, en particular, $D(\gamma'_m)$, $D(\gamma'_{m+1})$ no son disjuntos. Si $D(\gamma'_m)\subseteq D(\gamma'_{m+1})$, podríamos aplicar el lema 6 a $\gamma'_{m+1}$ (dentro de $C_m$) y encontrar $k$ tal que $D(\gamma'_{m+1})\subseteq D(\delta_{m,k})$. Entonces, tendríamos \[ D(\delta_{m,j}) = D(\gamma'_m) \subseteq D(\gamma'_{m+1}) \subseteq D(\delta_{m,k}). \] Por haber supuesto la maximalidad de $D(\delta_{m,j})$, tenemos $k=j$, por lo que $D(\gamma'_m)=D(\gamma_{m+1})$. Esto es imposible pues los radios $r_m$, $r_{m+1}$ son diferentes. La única posibilidad restante, por el lema 1, es que $D(\gamma_{m+1})\subseteq D(\gamma'_m)$.

Las condiciones $|\gamma'_m|\to0$, $\overline{\gamma}'_m\cap\overline{\gamma}'_{m+1}=\emptyset$ ahora son inmediatas, y tenemos $\{\gamma'_m\}$ como la cadena anidada propia que buscábamos que dominara a $\{\gamma_n\}$.

▢

4. La demostración

Ya tenemos listo todo para demostrar el resultado principal.

Demostración del teorema de Carathéodory.

Consideremos cualquier final primo $P\in\partial\widehat D$. Sea $p$ cualquier punto de acumulación de una cadena propia $\{\gamma_n\}$ que defina a $P$. Ahora, sea $r_n\to0$ una sucesión como en el corolario a la proposición 1. Por el lema 7, podemos suponer que $\gamma_n$ es un arco de círculo de radio $r_n$ centrado en $p$. La longitud de $f(\gamma_n)$ tiende a cero cuando $n\to\infty$, lo cual implica que es finita, por lo que la curva simple $f(\gamma_n)$ tiene extremos bien definidos en $\partial D'$. Por lo tanto, la sucesión $\{f(\gamma_n)\}$ es una cadena anidada de cortes transversales de $D'$. No sabemos si es o no una cadena propia pero, por el lema 7, por lo menos la domina una cadena propia $\{\gamma'_n\}$ que también podemos suponer que se forma por arcos de círculos con el centro en un punto de acumulación $p'$ de $\{f(\gamma_n)\}$. Además, escogemos los radios $r_n'$ como en el corolario. Luego, por el mismo razonamiento, la sucesión $\{f^{-1}(\gamma'_n)\}$ es una cadena anidada en $D$, y una tercera aplicación del lema 7 nos dice que la domina una cadena propia $\{\delta_n\}$.

Por esta construcción, se ve automáticamente que $\{\delta_n\}$ domina a $\{\gamma_n\}$, por lo que estas cadenas son equivalentes. Este hecho garantiza que el final primo $P'\in\partial\widehat D'$ determinado por $\{\gamma'_n\}$ no depende de nuestras elecciones de $p$, $r_n$ ó $\gamma'_n$. También garantiza que el proceso inverso asociará $P$ a $P'$, haciendo que la correspondencia sea 1-a-1. Finalmente, la existencia de las inclusiones especificadas en el enunciado del teorema se sigue por construcción.

▢

Esto termina la demostración del teorema de Carathéodory. Para la segunda versión, sólo se trata de ver qué son los puntos finales del disco $\Delta$. A cada punto $q$ sobre la circunferencia unitaria $\partial\Delta$, le asociamos el final primo $Q$ de $\Delta$ determinado por la cadena anidada propia $\{|z-q|=1/n\}\cap\Delta$. Por el lema 7, todos los finales primos se representan de esta forma. En otras palabras, se identifica $\partial\widehat\Delta=\partial\Delta$ de manera natural.

5. Consecuencias concretas

Es muy elegante tener una construcción que es invariante bajo transformaciones en la frontera pero, más allá del atractivo de la abstracción, el teorema de Carathéodory rinde mucha información concreta. Aquí están algunos de estos resultados.

A. La topología en el espacio de los puntos finales.

Sea $p\in\partial\widehat D$, definido por la cadena propia $\{\gamma_n\}$. Llamaremos cualquier dominio $D(\delta)$ que contenga a algún $D(\gamma_n)$ una prevecindad de $P$, y diremos que $P$ se adhiere a $D(\delta)$. Con esta terminología, definimos que un subconjunto $V$ de $\widehat D$ es abierto cuando (1) $V\cap D$ es abierto, y (2) para cada $P\in v\cap\partial\widehat D$ (si es que hay), existe una prevecindad $D(\delta)$ de $P$ tal que $V$ contiene tanto a $D(\delta)$ como a todos los puntos finales $Q$ que se adhieren a $D(\delta)$.

Los conjuntos abiertos así definidos definen una topología en $\widehat D$, en la cual $D$ es un abierto que hereda su topología usual de $\widehat D$. El teorema de Carathéodory dice ahora que la extensión $f\colon\widehat D\to \widehat D'$ es un homeomorfismo. La identificación $\widehat\Delta=\overline\Delta$ que dimos arriba también es un homeomorfismo. Por lo tanto, para cualquier región simplemente conexa $D$, el espacio $\widehat D$ es homeomorfo a un disco cerrado.

B. Comportamiento de una transformación conforme en la frontera.

Hasta ahora el desarrollo sigue siendo bastante abstracto. ¿Qué nos dice realmente acerca de la posibilidad de extender una transformación conforme $f\colon\Delta\to D$ a la frontera $\partial\Delta$ (o una parte de ella) como una verdadera función en el plano?

En otras palabras, fijemos $q\in\partial\Delta$. Al considerar todas las sucesiones $\{z_n\}$ en $\Delta$ que convergen a $q$, ¿cuáles son los posibles puntos límite de $\{f(z_n)\}$? Estos límites forman lo que se llama el conjunto de acumulación $\Lambda(f,q)\subseteq{\mathbb{C}}$ de $f$ en $q$.

Eso fue desde el punto de vista de $\Delta$. Veamos la perspectiva de $D$: si $P$ es un final primo de $D$, su impresión $I(P)$ es la intersección de las clausuras $\overline{D(\gamma_n )}$, donde $\{\gamma_n\}$ define a $P$. La impresión es un subconjunto no-vacío, compacto y conexo de $\partial D$; su definición no depende de la elección de $\{\gamma_n\}$.

La segunda versión del teorema de Carathéodory nos habla del maravilloso hecho de que cuando $P$ corresponde a $q$ bajo $f$, tenemos $\Lambda(f,q)=I(P)$. Por ende, $f$ puede extenderse continuamente a $\partial\Delta\cup\{q\}$ precisamente cuando $I(P)$ se forma de un solo punto. Cuando $p\in\partial D$, por definición, $p$ es un límite de alguna sucesión $\{w_n\}$ en $D$ y, entonces, una subsucesión de las preimágenes $\{f^{-1}(w_n)\}$ convergerá a algún punto $q\in\partial\Delta$. Esto implica $p\in\Lambda(f,q)$, lo cual muestra que todo punto de $\partial D$ está en la impresión de algún final primo. Esta propiedad es intrínsica a la región $D$. Sin embargo, no creo que sea tan fácil de demostrar sin hacer referencia a una transformación conforme.

C. Preimagen de una curva.

Otra de las muchas consecuencias del teorema de Carathéodory es que cuando una curva $\alpha$ en $D$ tiene un extremo bien definido $p\in\partial D$, su preimagen $f^{-1}(\alpha)\subseteq\Delta$ tiene un extremo bien definido $q\in\partial D$. Para verlo, toménse círcunferencias concéntricas $C_n$ que se contraigan a $p$; el último punto de intersección de $\alpha$ con $C_n$ en su camino hacia $p$ nos dice cuál arco $\gamma_n$ de $C_n\cap D$ queremos para formar la cadena anidada propia, cuyo punto final corresponde (por el teorema de Carathéodory, desde luego) al extremo $q$ de $f^{-1}(\alpha)$. Este resultado, demostrado por otros argumentos, se usa a veces como punto inicial de la teoría de los puntos finales.

D. Dominios de Jordan.

Ahora suponemos que la región $D$ es un dominio de Jordan, o sea, existe un homeomorfismo $h\colon\partial\Delta\to\partial D$. Cada corte transversal $\gamma$ de $D$ separa la curva $\partial D$ en dos subarcos $\beta_1$, $\beta_2$ tales que los dominios de Jordan con fronteras $\gamma\cup\overline{\beta}_1$, $\gamma\cup\overline{\beta}_2$ son lo que hemos llamado $D(\gamma)$, $E(\gamma)$ (sólo hay que cuidar que $b_0\notin\gamma$). Puesto que las curvas de Jordan son compactas, sabemos que tanto $h$ como $h^{-1}$ son uniformemente continuas. Esto implica que, dado $\epsilon>0$, cualquier par de puntos de $\partial D$ lo suficientemente cercanos se pueden juntar por un subarco de $\partial D$ de diámetro menor que $\epsilon$ (no puedo hablar de la longitud del subarco, pues $\partial D$ podría ser un fractal, pero el diámetro no es problema). Por lo tanto, para cualquier cadena anidada propia $\{\gamma_n\}$ en un dominio de Jordan, se tiene $|D(\gamma_n)|\to0$. Esto implica que para un dominio de Jordan, la impresión de cada final primo consiste de un solo punto. Ya sabemos que cada punto de $\partial D$ está en alguna impresión; luego, para completar la identificación de $\partial D$ con $\partial\widehat D$, basta mostrar que, cuando $I(P)=I(P')=\{p\}$, se sigue $P=P'$. Para verlo, representemos los finales primos por $\{\gamma_n\}$, $\{\gamma'_n\}$. Fijemos $n$ arbitrariamente y tomemos $n$ tan grande que $\overline{\gamma}_n\cap\overline{\gamma}'_n=\emptyset$. Entonces, las curvas de Jordan $\partial E(\gamma_n)$, $\partial D(\gamma'_m)$ son disjuntas. Entonces los dominios de Jordan $E(\gamma_n)$, $D(\gamma'_m)$ también son disjuntos, puesto ninguno contiene la clausura del otro. En otras palabras, $D(\gamma'_m)\subseteq D(\gamma_n)$; $\{\gamma_n\}$ domina a $\{\gamma'_n\}$; $P=P'$. En resumen: una transformación conforme de dominios de Jordan se extiende a un homeomorfismo de los dominios cerrados.

E. Extensión a un homeomorfismo de la esfera.

Cerramos con el resultado que dice que este homeomorfismo puede extenderse mucho más allá de la frontera.

Demostración. Sea $D$ la componente conexa acotada de ${\mathbb{C}}\setminus\Gamma$, así la otra es ${\mathbb{C}}\setminus\overline{D}$. Sean $f\colon\Delta\to D$, $g\colon{\mathbb{C}}\setminus\overline{\Delta}\to {\mathbb{C}}\setminus\overline{D}$ transformaciones conformes que nos da el teorema de Riemann. Sabemos, por el resultado D, que $f$ y $g$ se extienden continuamente a los conjuntos cerrados $\overline{\Delta}$, ${\mathbb{C}}\setminus\Delta$. Se define \[ h(z)=\left\{ \begin{array}{ll} f(z),\quad &z\in\overline{\Delta},\\ g(r\,g^{-1}(f(e^{i\theta}))),\quad& z=re^{i\theta}\in{\mathbb{C}}\setminus\Delta. \end{array} \right. \] En el borde común $z\in\partial\Delta$, estas definiciones concuerdan, y $h$ es el homeomorfismo deseado.

▢

6. Regiones no acotadas

Todo lo anterior se aplicará para las regiones no acotadas con la sencilla modificación de reemplazar la métrica euclidiana con la métrica esférica. La distancia esférica $[z,w]$ entre $z,w\in{\mathbb{C}}$ es $|z-w|/\sqrt{(1+|z|^2)(1+|w|^2)}$. Con esto ajustamos la noción de “diámetro” en los lemas 5, 6, 7 y encontramos que los resultados topológicos se siguen con las mismas demostraciones.

Para el lado analítico, hay que usar los elementos de longitud $1/(1+|z|^2)$ y de área $1/(1+|z|^2)^2$. Ahora escribimos $C_r$ para el “círculo” de centro $p\in{\mathbb{C}}$ con radio esférico $f$ (necesariamente $r< 1/2$), y $\ell(r)$, $\lambda(r)$ para las longitudes esféricas de $C_r\cap D$, $f(C_r\cap D)$. Parametricemos $C_r$ por $z =C_r(s)$ donde $s$ mide longitud de arco esférica, o sea, $|C_r'(s)|=|dz|/ds=1+|z|^2$. Entonces, \[ \ell(r)=\int_{E_r}ds, \quad \lambda(r) = \int_{E_r}\frac{|f'(z)|}{1+|f(z)|^2}|C_r'(s)|\,ds , \] donde $E_r$ es una unión de intervalos en la variable $s$. Se calcula que la longitud esférica de $C_r$ es $\pi\sin2r$, por lo que $\ell(r)\le\pi\sin2r< 2\pi r$. De la desigualdad de Cauchy-Schwarz se puede ver que $\lambda(r)^2$ no es mayor del producto de dos integrales específicas, una de las cuales es precisamente $\ell(r)$. Al dividir por este factor y volver a integrar, \[ \int_R^{R'} \frac{\lambda(r)^2}{2\pi r}dr \le \int_R^{R'} \!\!\! \int_{E_r} \frac{|f'(z)|^2}{(1+|f(z)|^2)^2}(1+|z|^2)^2 \,ds\,dr. \] Como $dr$ y $ds$ son ortogonales, $ds\,dr$ mide el área esférica (cerca de $z\in D$), y $(1+|z|^2)^2\,ds\,dr=dx\,dy$ es el área euclideana. Por lo tanto, la integral a la derecha es igual al área esférica de una parte de $f(D)$, que siempre es finita. Así se adapta la proposición 1 y su corolario para regiones imagen $f(D)$ arbitrarias.

Bibliografía comentada

[1]  Ahlfors, L. V. Complex analysis. An introduction to the theory of analytic functions of one complex variable. 3a ed. International Series in Pure and Applied Mathematics. McGraw-Hill Book Co., New York, 1978.

[2]  Ahlfors, L. V. Conformal invariants. Topics in geometric function theory. AMS Chelsea Publishing, Providence, 2010.

[3]  Beardon, A. F. Complex analysis. The argument principle in analysis and topology. John Wiley & Sons, Ltd., Chichester, 1979.

[4] Behnke, H., Sommer, F. Theorie der analytischen Funktionen einer komplexen Veränderlichen. Springer-Verlag, Berlin-Göttingen-Heidelberg, 1962.

[5] Burckel, R. B. An introduction to classical complex analysis. Vol. 1, Pure and Applied Mathematics, 82, Academic Press, Inc. New York-London, 1979.

[6] Carathéodory, C. Über die Begrenzung einfach zusammenhängender Gebiete, Math. Ann. 73, 323-370 (1913).

[7] Carathéodory, C. Theory of functions of a complex variable. Vol. 2, Chelsea Publishing Company, New York, 1954.

[8]  Carathéodory, C. Conformal representation. 2a ed. Cambridge Tracts in Mathematics and Mathematical Physics 28 Cambridge, 1952.

[9]  Goluzin, G. M. Geometric theory of functions of a complex variable. Translations of Mathemaical Monographs, Vol. 26, American Mathematical Society, Providence, R.I., 1969.

[10]  González, M. O. Complex analysis. Selected topics. Monographs and Textbooks in Pure and Applied Mathematics 152, Marcel Dekker, Inc., New York, 1992.

[11]  Hille, E. Analytic function theory. Vol. II, Ginn and Co., Boston-New York-Toronto, 1962.

[12]  Lang, S. Complex analysis. Addison-Wesley Publishing Co., Reading-London-Amsterdam, 1977.

[13] Lelong-Ferrand, J. Représentation conforme et transformations à intégrale de Dirichlet bornée. (francés) Gauthier-Villars, Paris, 1955.

[14] Markushevich, A. I. Theory of functions of a complex variable., Vol. III. Prentice-Hall, Inc., Englewood Cliffs, N.J., 1967.

[15]  Nevanlinna, R., Paatero, V. Introduction to complex analysis. segunda ed., New York: Chelsea, 1982.

[16]  Novinger, W. P. An elementary approach to the problem of extending conformal maps to the boundary, Amer. Math. Monthly 82 (1975) 279–282.

[17]  Palka, B. P. An introduction to complex function theory. Undergraduate Texts in Mathematics. Springer-Verlag, New York, 1991.

[18]  Pommerenke, C. Univalent Functions. Vandenhoeck & Ruprecht, Göttingen, 1975.

[19]  Rudin, W. Real and complex analysis. 3a ed. McGraw-Hill Book Co., New York, 1987.

[20]  Schlesinger, E. C. Conformal invariants and prime ends, Amer. J. Math. 80 (1958) 83–102.

[21]  Tsuji, M. Potential theory in modern function theory. Reimpresión de la edición de 1959. Chelsea Publishing Co., New York, 1975.