

Existen varias maneras de imaginar “el infinito” en el plano $\mathbb{R}^2$.
Si el plano $(x,y)$ se piensa como el plano de los números complejos $\mathbb{C}=\{ z=x+y\sqrt{-1} \}$, el infinito es un solo punto $\infty$; el conjunto $\mathbb{C}\cup\{\infty\}$ es la esfera de Riemann.
Otro modo de añadir “el infinito” al plano es requerir que cada par de rectas siempre se intersecten en un punto. Para esto, se necesita unir a $\mathbb{R}^2$ un punto por cada familia de rectas paralelas en el plano; así, cada par de rectas paralelas tendrá un punto de intersección al infinito. Los puntos al infinito forman todo un “círculo al infinito”; el plano, junto con su círculo al infinito, se conoce como “el plano proyectivo”.
Otro modo muy diferente de añadir un círculo al infinito a un plano se usa en la geometría hiperbólica. La diferencia con el plano proyectivo es que el plano hiperbólico, junto con sus puntos al infinito, forma un disco, mientras el plano proyectivo no tiene frontera.
Los diagramas de Penrose permiten imaginar el infinito en el espacio-tiempo.
El espacio-tiempo vacío tiene una coordenada llamada “tiempo” y el resto de sus coordenadas son la coordenadas espaciales. En el caso de una sola coordenada espacial $x$, el espacio-tiempo es un plano $(x,t)$ donde $t$, por supuesto, es el tiempo.
El espacio-tiempo $(x,t)$ está dotado con la métrica de Minkowski: si $(X,T)$ y $(X',T')$ son dos vectores en el mismo punto del espacio-tiempo, su producto escalar es $$(X,T)\cdot (X',T') = XX'-c^2 TT',$$ donde $c$ es la velocidad de la luz. Como consecuencia, el intervalo entre dos puntos $(x,t)$ y $(x', t')$ del espacio-tiempo tiene la magnitud $$(x-x')^2 - c^2(t-t')^2.$$ Los físicos teóricos suelen escoger sus unidades de medición de tal suerte que $c=1$ (y, en particular, los intervalos de tiempo se miden en las mismas unidades que las distancias); en estas unidades, esta magnitud es igual a $$(x-x')^2 - (t-t')^2$$ (a diferencia del cuadrado de la distancia euclidiana, el cual es igual a $(x-x')^2 + (t-t')^2$). Si dos puntos en el espacio-tiempo pertenecen a la misma trayectoria de la luz, el intervalo entre ellos tiene magnitud cero.
Aunque el espacio-tiempo $(x,t)$ es infinito, existe una transformación conforme (es decir, que preserva los ángulos, definidos mediante el producto escalar de Minkowski) que lo transforma en una figura finita:
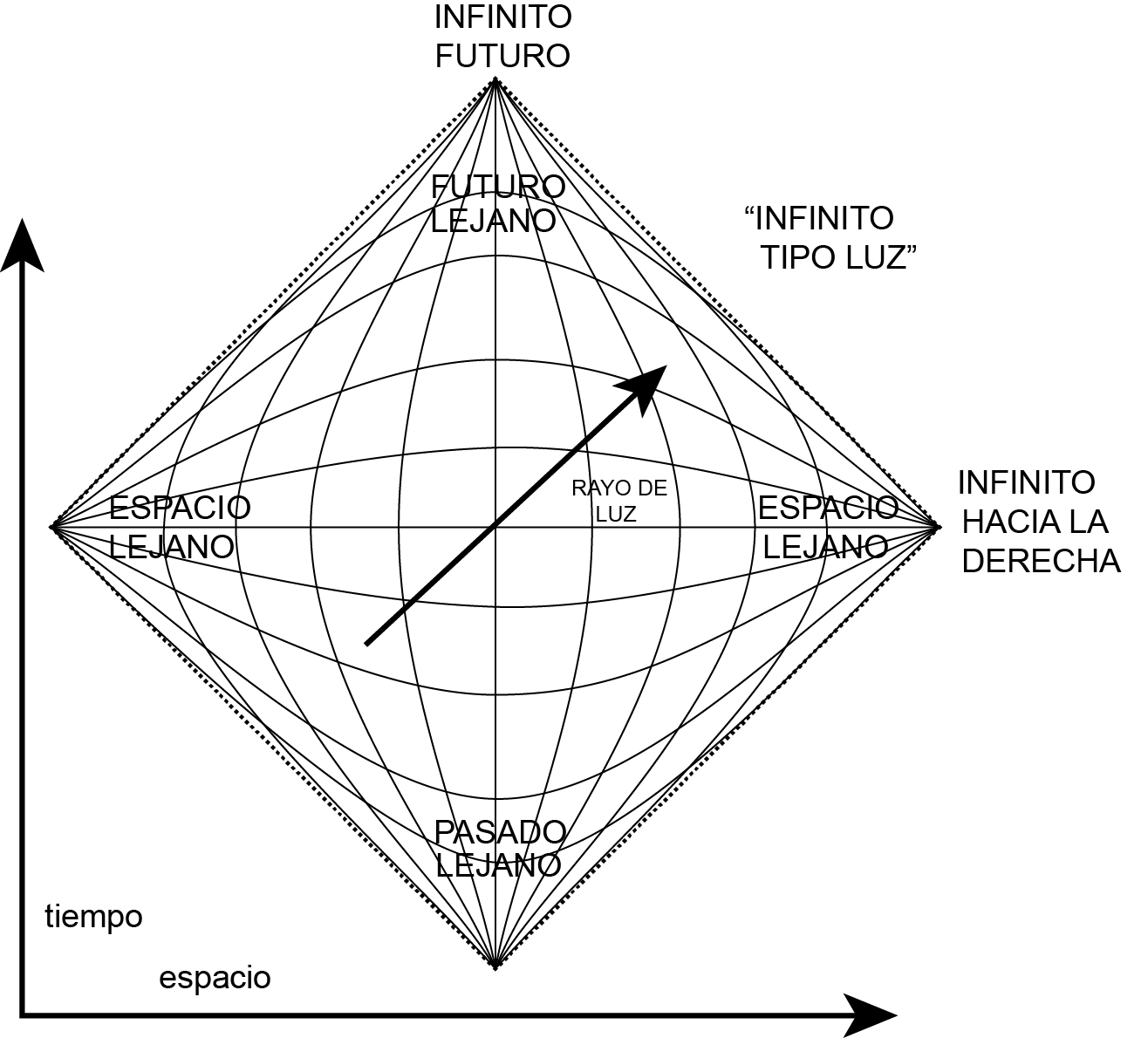
El borde del rombo que representa el espacio-tiempo corresponde al infinito. Existe un punto para el futuro y uno para el pasado, un punto infinitamente lejano hacia la derecha y uno hacia la izquierda. Se puede pensar que los puntos en el infinito forman unas trayectorias de la luz; la distancia de Minkowski entre ellos es cero.
El espacio-tiempo del universo físico no es vacío; según la teoría de la gravedad de Einstein, la existencia de las masas cambia su geometría. En particular, hay objetos cuya existencia introduce nuevos infinitos en la geometría del espacio-tiempo: son los agujeros negros. Los infinitos producidos por los agujeros negros son los horizontes de los agujeros: son las superficies en el espacio pasando las cuales ya no es posible regresar.
La teoría de Einstein admite varios tipos de agujeros negros: agujeros estacionarios o los que se forman mediante un colapso gravitacional, neutrales o con carga eléctrica. En todos estos casos, el espacio-tiempo que contiene un agujero negro se puede transformar de manera conforme (preservando ángulos) en una figura que consiste en partes acotadas. Una representación plana de esta figura se llama “diagrama de Penrose del agujero negro”.
Los diagramas de Penrose de los agujeros negros contienen una novedad: el espacio-tiempo en la presencia de los agujeros negros está dividido en partes desconectadas. Los infinitos ya no necesariamente están en el borde del diagrama de Penrose; por ejemplo, el horizonte separa dos regiones del diagrama de Penrose de un agujero negro. Sin embargo, la transición entre estas regiones no es algo que se puede contemplar fácilmente: detrás del horizonte de un agujero negro el espacio se intercambia con el tiempo.
El tipo más sencillo de agujeros negros es el agujero tipo Schwarzschild: un agujero negro estacionario sin carga. Su diagrama de Penrose se ve de la siguiente manera:
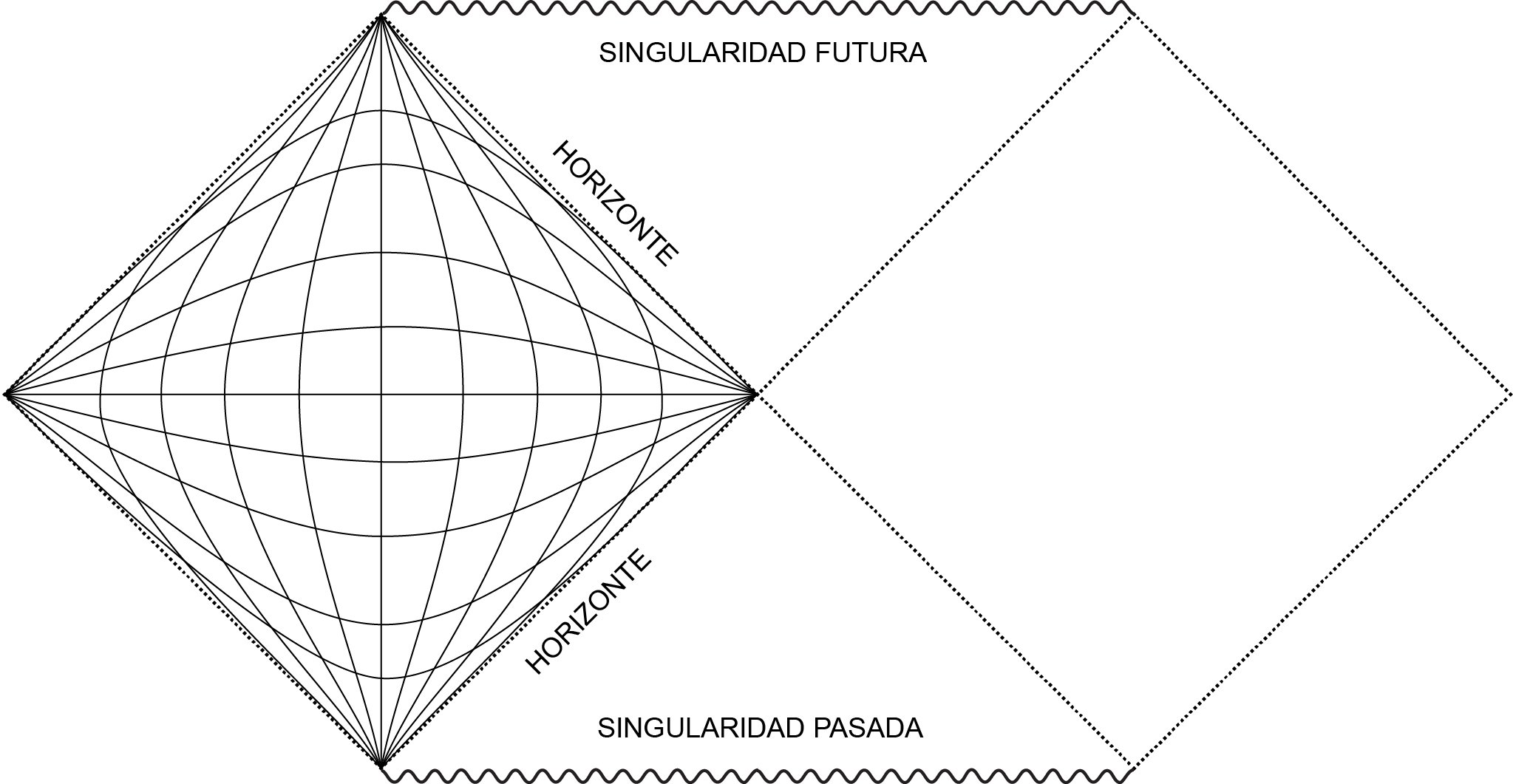
Los dos triángulos en este diagrama corresponden a la región alrederor del centro del agujero negro; es inaccesible en el sentido de que un observador nunca podrá ver cómo un objeto cruza el horizonte. El rombo del lado derecho es un universo paralelo que existe como parte de la solución a las ecuaciones de Einstein. No hay modo de confirmar o refutar su existencia física.
Los diagramas de Penrose para los agujeros negros de otros tipos pueden ser aún más complejos e involucrar un número infinito de universos.