Los ritmos irracionales de Conlon Nancarrow

“Favor de no disparar al pianista. Hace lo que puede.”

Oscar Wilde observó este letrero en un saloon en Leadville, Colorado en 1882 (y comentó que éste fue “el único método racional de la crítica de arte que jamás había visto”). El público estadunidense exigía entretenimiento de calidad; era una demanda difícil de satisfacer. Cuando a finales del siglo XIX, el piano mecánico (conocido como pianola, por una de las primeras marcas de este aparato) apareció en el mercado, tuvo un éxito espectacular.

La pianola se podía usar como un piano usual y, también, para reproducir música grabada; incluso, simultáneamente. La música se representaba con unos agujeros en rollos de papel; cada agujero correspondía a una tecla del piano. Ciertos modelos también usaban agujeros especiales en los márgenes de los rollos para codificar las características adicionales de la intepretación, tales como volumen, tempo etcétera.

Para los años veinte, la pianola se usaba extensamente; sobre todo, para el jazz. Era menos popular como un medio para reproducir la música clásica: pese a toda su precisión, le faltaba alma. Igor Stravinsky consideró la posibilidad de usar pianolas en su obra Les Noces, pero desistió ante la dificultad de sincronizar los instrumentos mecánicos con el coro y terminó usando cuatro pianos (existe una grabación de Les Noces que retoma la idea original de Stravinsky; la parte de los pianos está hecha en computadora con el sonido cercano al de un piano mecánico).

La llegada de la radio y la Gran Depresión acabaron con las pianolas: en 1932 la producción de los pianos mecánicos en Estados Unidos se paró. Sin embargo, uno de los episodios más interesantes en la historia de este instrumento todavía estaba por empezar: Conlon Nancarrow comenzó a perforar sus rollos para pianola en la Ciudad de México a finales de los 1940.

Nancarrow nació en Texarkana, Arkansas, en 1912. Tocó trompeta en una banda de jazz; después, estudió música: primero, en Cincinatti y, después, en Boston. Se afilió al partido comunista y participó en la guerra civil española. Al regresar a los Estados Unidos, se topó con discriminación por parte del gobierno y decidió emigrar a México. Desde 1940 y, hasta su muerte en 1997, vivió en la Ciudad de México, en la colonia Las Águilas. A partir de 1956 fue ciudadano mexicano.

Desde el principio, Nancarrow encontró un obstáculo para la intepretación de sus obras musicales: los músicos. La complejidad de sus partituras era abrumadora; las presentaciones exitosas de sus obras eran raras. En cambio, la precisión de la pianola no solo excluía los errores, permitía escribir música inaccesible a los intérpretes humanos (los problemas con los músicos no siempre se debían a la complejidad: en una ocasión, los músicos se rehusaron a tocar una obra de Nancarrow porque no querían que el público pensara que “tocaban notas equivocadas”). Probablemente, la primera obra de Nancarrow escrita para pianola fue la Boogie-Woogie Suite, o el Estudio Número 3:

El fenómeno que Nanacarrow exploraba en su música era la interacción de ritmos. Sus obras para pianola, llamadas “estudios”, utilizan la forma de canon mensural. Un canon usual consiste en varias voces que llevan la misma melodía y siguen una a la otra separadas por un intervalo de tiempo. En un canon mensural, las voces no solamente pueden estar separadas en el tiempo sino, además, llevan la misma melodía con velocidades (o tempi, plural del tempo) diferentes; un ejemplo clásico de canon mensural es Le ray au soleyl, de Johannes Ciconia, del siglo XIV.

Nancarrow comenzó experimentando con las proporciones de los tempi relativamente sencillas, como $4:5$ o $3:4$. En sus composiciones posteriores, el patrón rítmico se complica: el Estudio 31 usa la proporción $21:24:25$, en el Estudio 37, la proporción es de $1: 15/14 : 9/8 : 6/5 : 5/4: 4/3: 7/5: 3/2 : 8/5 : 5/3 : 7/4 : 15/8$. Aparecen las proporciones irracionales: $2: \sqrt{2}$ en el Estudio 33, $e:\pi$ en el Estudio 40, $\frac{1}{\sqrt[3]{\pi}} : \sqrt[3]{\frac{13}{16}}$ en el Estudio 41a. En varios de los estudios, los tempi son variables; el Estudio 44 no especifica la proporción de tempi, la cual se puede escoger arbitrariamente.

El siguiente video es una visualización del Estudio 24; se pueden apreciar variaciones de los tempi de las tres voces:

Notemos que, en esta composición, no existe un órden definido de las voces, a diferencia de lo que ocurre en un canon usual.

Detrás de las experimentaciones con las relaciones irracionales de tempi, un matemático reconoce el siguiente teorema:

Traducido al lenguaje de la música, este teorema significa que, si dejamos correr juntos, por un tiempo muy largo, dos ritmos cuyas velocidades están en una proporción irracional, el patrón rítmico que consiste en los pulsos de ambos ritmos incluirá intervalos de todas las duraciones posibles.

Por supuesto, los Estudios de Nancarrow son de longitud finita y no tiene sentido hablar de proporciones irracionales en la vida real: cualquier medición es una aproximación. Sin embargo, la complejidad rítmica de la obra de Nancarrow es evidente e impresionante. Por ejemplo, así suena la proporción $e:\pi$ :

Por décadas, el trabajo de Nancarrow fue apreciado por muy pocos. György Ligeti escribía: Esta música es el descubrimiento más grande desde Webern e Ives ... ¡algo grande e importante para toda la historia de la música! Su música es tan absolutamente original, disfrutable, perfectamente construida pero, al mismo tiempo, emocional ... para mí, es lo mejor de cualquier compositor hoy vivo. Sin embargo, el público general no conoció la música de Nancarrow hasta 1969, cuando salió un disco con sus obras en Columbia Records. A esta grabación (de mala calidad) le siguió, ocho años después, una colección de cuatro discos en 1750 Arch Records, la cual contenía todos los Estudios Para la Pianola. En los años 1980, la fama de Nancarrow comenzó a crecer (aunque fuera de México) y, después de muchos años de escribir solamente para la pianola, Nancarrow volvió a escribir para intérpretes humanos. Por supuesto, la estructura rítmica de estas obras no incluye proporciones tan exorbitántemente complicadas de tempi como los estudios para pianola; sin embargo, Nancarrow siguó usando cánones mensurales. Por ejemplo, en el Cuarteto Número 3 aparecen cánones 3:4:5:6 :

El interés por la música de Nancarrow sigue creciendo; irónicamente, Nancarrow utilizaba un aparato ya obsoleto para crear la música que iba muy adelante de su tiempo. Dada la escasez de pianolas y la dificultad de su transportación, Nancarrow tenía en mente que, para ser reproducidas frente al público, sus obras debían grabarse en cinta magnética en su estudio. Ahora, gracias a los esfuerzos del Dr. Jürgen Hocker (1937-2012), quien publicó una impresionante colección de los estudios para pianola en youtube.com, tenemos la oportunidad de admirar cómo un rollo de papel entra al mecanismo de una pianola y los arreglos de agujeros se transforman en la demente y fascinante música de Conlon Nancarrow.

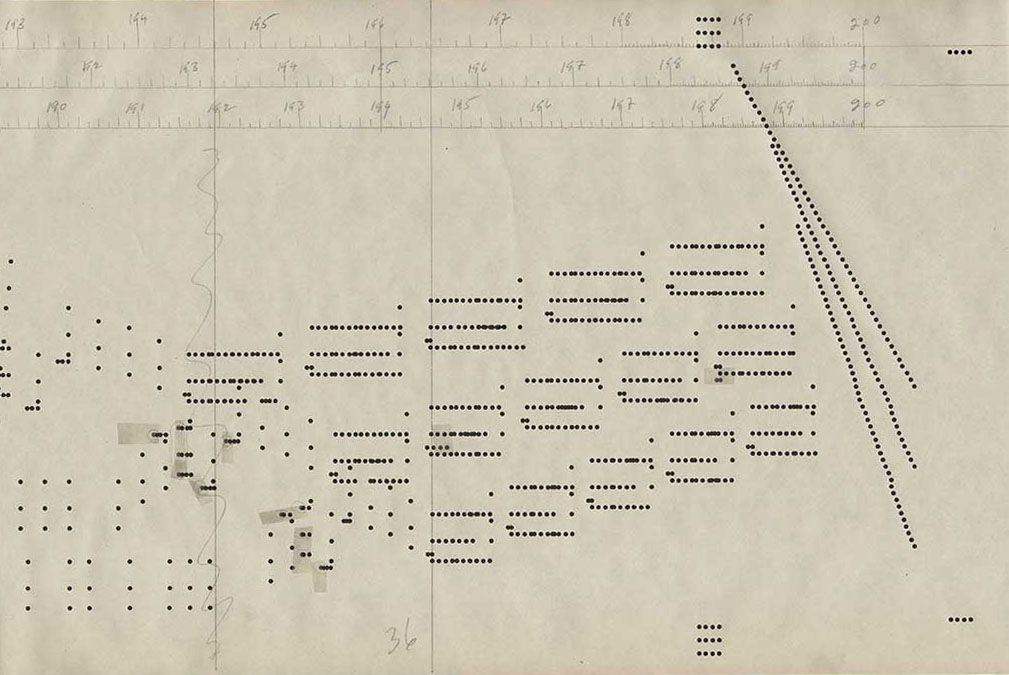
Las imágenes de este artículo provienen del sitio web “El compositor Conlon Nancarrow. La vida y la obra de un ermitaño mexicano” (en alemán, con contribuciones en inglés), por Jürgen Hocker, y se reproducen con el amable permiso de la Sra. Beatrix Hocker.