Sam Gitler fue una persona extraordinaria, un matemático del rango más alto, con energía y ambición abundantes, con una apreciación refinada de la calidad y con una calidez humana que conquistaba al instante.

Nos conocimos como estudiantes de posgrado en Princeton a finales de los cincuenta. Él había estudiado ingeniería en México pero sucumbió a los encantos de las matemáticas y a la influencia de las visitas a México del topólogo mundialmente famoso, Solomon Lefschetz, de Princeton.

Sam escogió a Norman Steenrod como su asesor. Steenrod tenía la reputación de una persona extremadamente organizada y metódica y demandaba las mismas cualidades de sus estudiantes, al grado de requerir que reescribieran sus tesis cinco o seis veces. Sam no se desanimó y perseveró con firmeza hasta obtener su doctorado.

Steenrod fue uno de los grandes innovadores en las matemáticas del siglo XX; descubrió un método nuevo en la topología algebraica con enorme sutileza y poder, el cual tuvo, durante años, una influencia inmensa. El trabajo temprano de Sam involucraba aplicaciones virtuosas de este método.

No hay esperanza de poder transmitir en un hora al público general ni siquiera una sombra de estos métodos y técnicas; en lugar de esto, trataré de describir el contexto y la naturaleza de algunos de los problemas resueltos por Sam.

Muchas veces, después de identificarme como “topólogo” en una conversación con un no-matemático, he intentado dar alguna descripción del campo matemático de la topología. Con frecuencia, digo “geometría flexible”.

Mientras que, en la geometría euclidiana en el plano, los triángulos, los cuadrados, los círculos son objetos muy diferentes, si permitimos que sean flexibles, se vuelven la misma cosa. Su tamaño deja de importar, el número o la rectictud de sus lados tampoco importan.

Estamos sentados en una mesa y se nos da una banda de hule y unos alfileres con el permiso de clavarlos en la mesa, y se nos pide hacer un diseño: insertamos unos alfileres en la mesa, estiramos la banda y la ponemos alrededor de ellos para delimitar un área. No se nos permite que la banda de hule cruce a sí misma.

Jugamos a la geometría (geometría plana) con la banda de hule estirada creando líneas rectas entre los alfileres, produciendo formas geométricas, triángulos, cuadriláteros, etccétera, pero sin importar dónde ponemos los alfileres, la topología no cambia, está determinada por la banda de hule en la mesa.

Uno de los métodos más fundamentales en las matemáticas y las ciencias en general es la técnica de ignorar casi todo, salvo el fenómeno estudiado. En topología, olvidamos las distancias, sólo preservamos la noción de la “cercanía” (continuidad).

La definición matemática precisa de la continuidad requirió doscientos años para desarrollarse (¿alguien quiere recordar épsilon-delta?); así que nos quedamos aquí con las nociones intuitivas.

Un panadero dinámico comienza con un pedazo de masa que corta en pedacitos más pequeños. Cada corte cambia el número de pedazos, cambiando, de este modo, la topología; cada corte causa que partes cercanas de masa de repente se encuentren lejos una de la otra.

El número de pedazos es un ejemplo de lo que se llama “invariante topológico”, un número que solamente depende de la topología.

El panadero dinámico comienza a girar la masa en el aire sobre su dedo y el pedazo redondo se comienza a aplanar y expandirse hacía la forma correcta de una pizza. La topología de la masa no se cambia; las partes cercanas siguen siendo cercanas, aunque posiblemente no igual de cercanas.

Un panadero aprendiz que intenta este proceso puede, por falta de experiencia, permitir que su dedo penetre la masa dejando un agujero en el medio y cambiando la topología, cuando los puntos en el medio se mueven hacia el borde interior del agujero (dejando de ser cercanos); en lugar de una pizza, parece que está haciendo alguna extraña especie de dona. Una “dona” de masa es topológicamente diferente de un pedazo de masa o de una pizza. Si una dona se corta con un cuchillo a través del agujero, un corte produce un solo pedazo de la masa. Cualquier corte de este pedazo de masa produce más de una pieza.

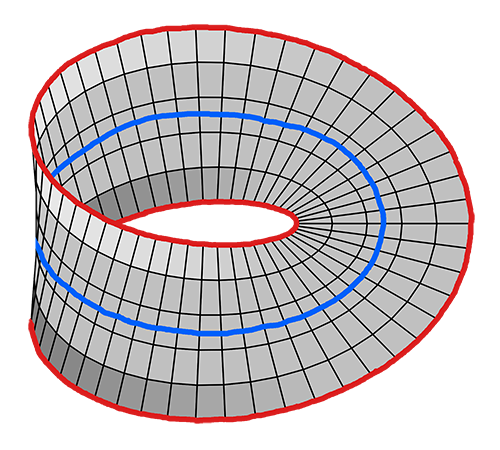
La pizza es un fenómeno tridimensional. Un ejemplo muy interesante en nuestras tres dimensiones es la banda de Moebius. Uno toma cierta longitud de un listón y pega sus extremos con una media vuelta. Sin esta vuelta obtendríamos un collar o un tubo (las dos palabras denotan objetos topológicamente idénticos, pero con connotaciones diferentes de tamaño y anchura). Con la media vuelta encontramos que los dos bordes del listón están ahora conectados; así que la banda de Moebius sólo tiene un borde y un solo lado. Y el único borde es, topológicamente, un círculo.

Voy con mi sastre (3-dimensional) y le pido coser un parche redondo al borde circular de la banda de Moebius. Él me dice, muy enojado, que esto es imposible y que, en el futuro, debo solicitar ayuda en alguna otra parte. Solicito lo mismo a mi sastre matemático, quien vive en el mundo de los conceptos; él cose el parche de inmediato y me lo regresa con una etiqueta que dice:

“Plano proyectivo: hecho a mano en espacio abstracto; sólo tintorería”.

¿Por qué no lo pudo lograr el sastre 3-dimensional?

Si uno desprende el hilo exterior (rojo) de la banda de Moebius y lo deja caer, éste no se caerá al piso sino quedará colgado de la banda. Si uno sólo mira el hilo rojo y el hilo azul que corre a lo largo del centro de la banda y se olvida del resto, se ve que (topológicamente) son lo mismo que dos aros entrelazados. Claramente, no se podría hacer una burbuja de jabón sobre uno de los aros porque el otro aro la poncharía. Así que, en nuestro espacio tridimensional, cualquier parche cuyo borde es el hilo exterior (rojo) sería cortado por el hilo central (azul) de la banda.

Mi sastre matemático me recomienda a un sastre hábil 4-dimensional. Él añade otra dimensión (¿tiempo?) al 3-espacio en el cual vivimos y lo observamos coser el parche. Deja que el hilo rojo se mueva lentamente al futuro formando un collar (color rosa) y dejando el resto de la banda de Moebius atrás, para adjuntarle un parche (rosa) que ya tiene listo, sin ninguna banda de Moebius que pueda interferir en esta situación (moderna).

(Dejaré a los filósofos la tarea de comentar sobre este método tan importante de resolver varios problemas en el mundo real.)

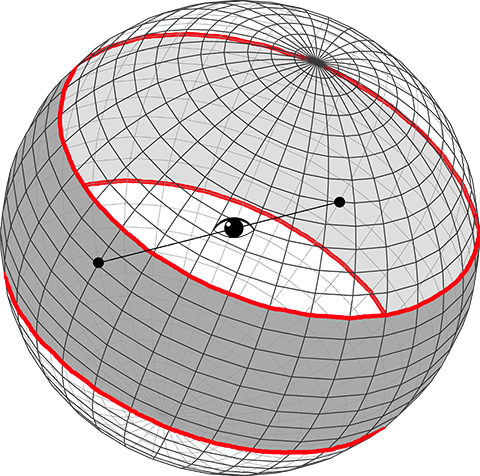
Consideremos un collar como la zona ecuatorial de un globo terráqueo e imaginemos a un observador en el centro del globo. Él es una versión matemática del mitológico Jano, quien tenía un ojo extra en la nuca. Nuestro Jano sólo tiene dos ojos, pero uno de ellos mira hacia adelante y el otro, hacia atrás. Debería ver dos imágenes, pero está condicionado (matemáticamente) para verlas como una sola. ¿Qué es lo que ve cuando mira la banda ecuatorial? El arriba de un lado es el abajo del otro y girar en el lado de frente es girar en la misma dirección en el otro lado.

¡Ve una banda de Moebius!

Pero él ve el hemisferio norte del mismo modo que el hemisferio sur. Así que, él simplemente ve un gran disco curvo pegado a una banda de Moebius. En lugar de la superficie del globo, Jano ve el Plano Proyectivo.

Es una descripción tridimensional, pero Jano experimenta las cosas de un modo no euclidiano. Su espacio tridimensional no es el nuestro.

Si colocamos a nuestro Jano en un espacio euclidiano de una dimensión más alta (digamos, la dimensión $n+1$) y él mira el cielo nocturno (una $n$-esfera), él verá lo que llamamos el Espacio Proyectivo Real de dimensión $n$ ($RP(n)$, para sus amigos). Lo “real” se refiere al hecho de que los parámetros que describen nuestro espacio euclidiano son números reales (y también para distinguirlo de la numerosas imitaciones baratas que abundan en el mercado).

Entonces, surge una pregunta: ¿cuál es el m más pequeño tal que el espacio euclidiano $R^m$ de dimensión $m$ (descrito por m parámetros reales) contiene una copia de $RP(n)$ (en este caso, decimos que $RP(n)$ se puede encajar en $R^m$)?

La descripción del caso de $RP(2)$ que dimos es muy vieja (o sea, “clásica”) pero, para las dimensiones más altas $n$, el número mínimo $m$ para un $n$ dado tal que $RP(n)$ se puede encajar en $R^m$ todavía, en general, es un misterio.