

Una vez, cuando mi colega Kendra Killpatrick se mudaba a la Universidad de Pepperdine, el chofer le hizo una pregunta de matemáticas. Supongamos que John y Bill tienen un vaso cada uno con cantidades diferentes de agua. John juega con el agua haciendo lo que llamaremos movimientos con popote; éstos consisten en la siguiente sucesión de manipulaciones (ver Figura 1). Primero, John toma un popote y lo baja verticalmente en su vaso hasta el fondo. Después, tapa el popote con el dedo y lleva el agua contenida en él al vaso de Bill, donde la suelta. De la misma manera, se podría definir un movimiento con popote del vaso de Bill al de John.
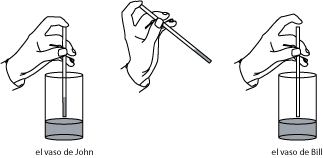
En [IK]K. Iga, K. Killpatrick, Truck drivers, a straw, and sharing a glass of water, College Mathematics Journal 37 (2006), no. 2, 82—92., la Dra. Killpatrick y yo consideramos sucesiones de movimientos con popote en una sola dirección (digamos, del vaso de John al de Bill) y, también, sucesiones en la cuales los movimientos desde el vaso de John se alternan con los movimientos desde el vaso de Bill. Determinamos las condiciones bajo las cuales se podía llegar a la situación donde ambos vasos tienen la misma cantidad de agua; además, estudiamos el comportamiento límite. En otro artículo, [I2]K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290., consideré sucesiones arbitrarias de movimientos con popote y determiné si era posible escogerlas para obtener el comportamiento límite que converja a cierto estado dado, o que tenga este estado como uno de sus puntos límites.
En el presente artículo, considero el siguiente problema. Supongamos que la sucesión de los movimientos entre los vasos se determina lanzando una moneda. Es decir, para cada movimiento lanzamos una moneda y, si sale águila, movemos el agua al vaso de John y, si sale sol, hacemos el movimiento hacia el vaso de Bill. ¿Qué se puede decir sobre la distribución de probabilidad en el límite?
Las simulaciones por computadora producen unas gráficas interesantes y muy extrañas que involucran la “escalera del diablo” de Cantor, la distribución uniforme y la distribución normal (las que se ven en las clases introductorias de probabilidad). Más allá de las simulaciones, las demostraciones rigurosas requieren estudiar las sutilezas de la convergenica de series (que dependen del órden de los términos) y conducen a una interesante familia de distribuciones, conocidas como las convoluciones de Bernoulli. Estas convoluciones fueron estudiadas desde los años treinta (en particular, por el matemático húngaro Paul Erdős) y siguen siendo un área activa de investigación; a su vez, están relacionadas con los números de Pisot-Vijayaraghavan, los cuales incluyen la razón dorada y aparecen en la teoría de los números “aleatorios” generados por computadora.
Usaremos la variable dinámica $x$ para representar la cantidad de agua en el vaso de John con las unidades escogidas de tal forma que $x=1$ corresponde a la situación cuando todo el agua está en el vaso de John.
Al igual que en [IK]K. Iga, K. Killpatrick, Truck drivers, a straw, and sharing a glass of water, College Mathematics Journal 37 (2006), no. 2, 82—92. y [I2]K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290., involucra un parámetro $r\in (0,1)$ que representa el área de la sección transversal del popote dividido por el área de la sección transversal del vaso. Un movimiento con popote del vaso de Jonh al vaso de Bill traslada la cantidad $rx$ de agua del vaso de John, mientras un movimiento del vaso de Bill mueve la cantidad $r(1-x)$ de agua.
Sea $s=1-r$; entonces, el cambio de $x$ como resultado de un movimiento hacía el vaso de Bill es dado por \begin{equation} f(x)=x-rx=sx\label{eqn:f} \end{equation} y el cambio de $x$ después de un movimiento hacia el vaso de John es: \begin{equation} g(x)=x+r(1-x)=sx+r.\label{eqn:g} \end{equation}
Imaginemos que, cada vez que vamos a efectuar un movimiento con popote, lanzamos una moneda para determinar si el movimiento va del vaso de John hacia el vaso de Bill o viceversa. Más formalmente, definamos una sucesión de variables aleatorias de Bernoulli independientes $B_0, B_1,\dots$ con $p=1/2$. Decir que son de Bernoulli con $p=1/2$ significa que, para cada $n$, $B_n$ puede tomar valores 0 o 1, con la probabilidad $1/2$ cada uno. El término “independiente” quiere decir que la probabilidad de un conjunto finito de valores $B_{I_1}=b_1, \dots, B_{I_k}=b_k$ (con los $B_I$ distintos) es el producto de las probabilidades correspondientes; en este caso es $(1/2)^k$.
Si denotamos por $x_0$ la cantidad inicial de agua en el vaso de John, podemos definir la variable aleatoria $X_0$ que toma el valor $x_0$ con probabilidad 1. Ahora, definamos las variables aleatorias $X_1,X_2,\dots$ usando la fórmula basada en (\ref{eqn:f}) y (\ref{eqn:g}) \begin{equation} X_{n+1}=s X_n+r B_n.\label{eqn:recurrence} \end{equation}
Podemos resolver esta relación de recurrencia (\ref{eqn:recurrence}) de la siguiente forma: \begin{equation} X_n=s^n x_0 + r\sum_{i=0}^{n-1} B_{n-i-1} s^i.\label{eqn:Bc} \end{equation} La probabilidad de que $X_n$ esté en el intervalo $[a,b]$ se escribe como $P(a\le X_n\le b)$ o $P(X_n\in [a,b])$ y la descripción de todas estas probabilidades para todos los intervalos $[a,b]$ es una distribución de probabilidad. Éstas se pueden describir usando una función de distribución cumulativa definida como: $F_{X_n}(t)=P(X_n\le t)$.
A veces, es conveniente utilizar la función de la densidad de probabilidad, definida como \[f_{X_n}(t) = \lim_{\epsilon\to 0} \frac{P(X_n \in [t-\epsilon,t+\epsilon])}{2\epsilon}.\] Este límite no siempre está bien definido, pero cuando lo está, su gráfica da un modo intuitivo de ver cómo la probabilidad se concentra alrededor de ciertos valores.
En el artículo [I2]K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290. quedó demostrado que la cantidad de agua en un vaso puede converger a un límite solamente si todos los movimientos con popote se hacen hacia el mismo vaso, con una cantidad finita de excepciones. La probabilidad de que esto suceda es cero, así que, con la probabilidad 1, $X_n$ no converge.
Sin embargo, esto no acaba con el problema. Puede ser $X_n$ no converja, pero veremos que la distribución de probabilidad de $X_n$, en efecto, converge. A saber, encontraremos $\lim_{n\to\infty} F_{X_n}(t)$.
Como un primer paso, podemos usar una computadora para modelar una sucesión de movimientos con popote. Fijemos un número $n$ de movimientos con popote y dividamos $[0,1]$ en compartimientos. Para cada una de las $2^n$ sucesiones posibles de movimientos con popote, usamos (\ref{eqn:Bc}) para encontrar el valor para $X_n$ y determinamos a qué compartimiento $X_n$ pertenece (aquí escogemos $x_0$ arbitrariamente, digamos $x_0=0$). Para cada compartimiento, contamos cuántos $X_n$ caen en él, convertimos este dato a probabilidad dividiendo por $2^n$ y, después, pasamos a la densidad de probabilidad dividiendo la probabilidad por la longitud del compartimiento correspondiente. Los detalles de este algoritmo se pueden ver en el apéndice.
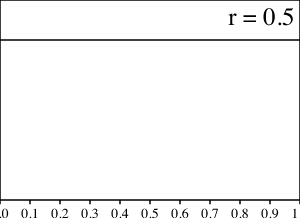
Para comenzar, tomemos $r=.5$. La función de la densidad que obtenemos se ve como la distribución uniforme en $[0,1]$:
Ahora, consideremos $r=1$. En este caso, el popote recoge todo el agua de un vaso y la traslada al otro. Después de cualquier número de movimientos con popote, $X_n=B_{n-1}$ será una variable aleatoria de Bernoulli con $p=1/2$.
Podríamos intentar $r=0$, pero, en este caso, los movimientos con popote no cambian nada, y $X_n$ siempre quedará en $x_0$, sea el que sea su valor.
Sin embargo, el límite $r\to 0$ es más interesante. Por ejemplo, podemos intentar $r=.1$. El resultado de los cálculos por computadora se parece más a la distribución normal, también conocida como la campana de Gauss:
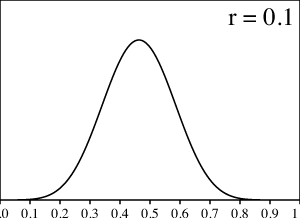
Aunque no mostramos aquí las gráficas correspondientes, resulta que cuando $r$ tiende a 0, la función densidad se parece más y más a la distribución normal, aunque para llegar a una gráfica precisa se necesitan más y más movimientos con popote y esto requiere un cálculo mucho más largo de lo que es factible hoy en día. Regresaremos a este tema en la Sección 9.
Entonces, si queremos saber a qué converge la probabilidad de $X_n$ para todo $r$, debemos contestar la siguiente adivinanza: ¿qué es lo que se ve como la distribcuión normal si $r$ es cercano a 0, como la distribución uniforme para $r=1/2$ y como una variable aleatoria de Bernoulli para $r=1$?
Para apoyar nuestra intuición, grafiquemos los resultados de los cálculos numéricos para varios valores de $r$ entre $0$ y $1/2$.
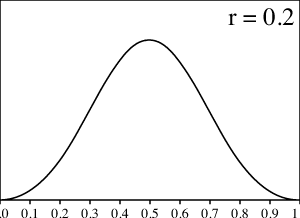
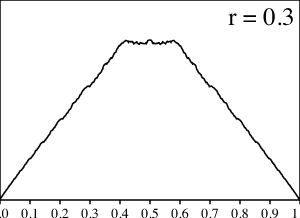
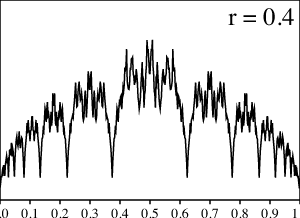
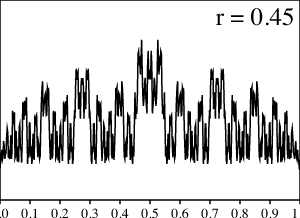
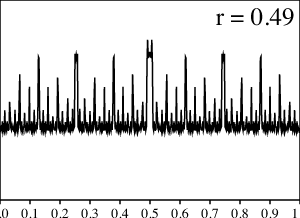
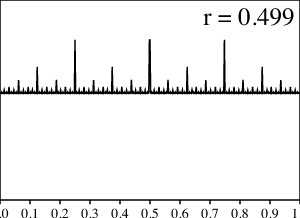
¿Qué sucede aquí? Para los valores pequeños de $r$ la gráfica se ve suave y cuando $r$ se aproxima a $1/2$, la gráfica se pone mucho más dentada. Sin embargo, tan pronto $r$ llega a $1/2$, ¡todas las asperezas, de repente, desaparecen en una distribución uniforme!
En lo que sigue, veremos que estas distribuciones son parte de una familia de distribuciones llamadas convoluciones de Bernoulli (éstas se describen en mayor detalle en Sección 4. Pero primero discutamos algunos casos especiales.
Como acabamos de ver, la simulación numérica sugiere que, en el caso $r=1/2$, obtenemos para $X_n$ la función de densidad de probabilidad que converge a la de la distribución uniforme. Esto es un hecho que podemos demostrar rigurosamente.
Como se ha demostrado en [I2]K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290., el resultado de hacer $n$ movimientos con popote puede expresarse en términos de expansiones binarias. Los $n$ movimientos se codifican en los primeros $n$ dígitos de la expansión binaria de $X_n$, donde los movimientos más recientes van primero. Así, el proceso aleatorio de decidir los movimientos con popote lanzando una moneda corresponde al escoger lo primeros dígitos de una expansión binaria por medio de lanzar una moneda. En el límite, podemos pensar en este proceso como en determinar un número real lanzando una moneda para obtener los dígitos sucesivos. Se sabe que el resultado es la distribución uniforme en $[0,1]$; es la distribución con la propiedad de que, para $[a,b]\subset [0,1]$, tenemos $P([a,b])=b-a.$ La función de densidad es $f(t)=1$ para $t\in[0,1]$ y 0 fuera de este intervalo.
La idea de la demostración es la siguiente.
Notemos, observando la expansión binaria, que, si dividimos el intervalo $[0,1]$ en $2^n$ segmentos iguales de la forma $[\frac{m}{2^n},\frac{m+1}{2^n})$, la probabilidad de $X_n$ de estar en cada uno de estos segmentos es igual a su longitud. Lo mismo se puede decir de cualquier unión de estos segmentos. Ahora, dado un intervalo $[a,b]$, para cada $n$ podemos aproximar $a$ y $b$ por números racionales $a_n$ y $b_n$ con el demoninador $2^n$.Ya tenemos que $P(X_n\in[a_n,b_n])=b_n - a_n$. Si tomamos $[a_n,b_n]\subset [a,b]$, estamos aproximando $P(X_n\in[a,b])$ por defecto. De la misma manera, si decidimos tomar $[a_n,b_n]\supset[a,b]$, obtenemos una aproximación $P(X_n\in[a,b])$ por exceso. Escogiendo las sucesiones $a_n, b_n$ de un modo apropiado, no es difícil de demostrar que $\lim_{n\to\infty} P(a\le X_n\le b)=b-a$, así que la distribución de probabilidad para $X_n$ converge a la distribución uniforme.
El caso $r>1/2$ también es accesible. En [I2]K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290. se ha visto que, para $r>1/2$, los únicos valores posibles de $X_n$, para $n$ suficientemente grande, pertenecen a cierto conjunto de Cantor. Este conjunto se define en términos de una sucesión de conjuntos: tomamos $J_0=[0,1]$ y, para cada $n>0$, definimos $J_n$ a partir de $J_{n-1}$ removiendo la parte de tamaño relativo $2r-1$ de cada intervalo. La longitud total de $J_n$ es $(2-2r)^n$ y tiende a $0$ cuando $n\to\infty$. Así, el conjunto de Cantor tiene longitud cero.
La densidad de probabilidad de $X_n$ está concentrada en $J_n$ y el área total bajo la curva de la densidad es 1. Conforme con el aumento de $n$, la longitud de $J_n$ decrece, entonces el valor de la densidad de probabilidad debe incrementar hacia el infinito. Es difícil discutir el comportaminto límite cuando la función tiende al infinito; entonces, en lugar de la densidad de probabilidad, consideraremos la función de distribución cumulativa $F_{X_n}(t)=P(X_n\le t)$, la cual siempre permanece finita.
En las gráficas que mostramos, tomamos $r=2/3$; la misma historia se repite para otros valores de $r>1/2$, con las longitudes de los intervalos ajustadas.
Ahora, tenemos que $F_{X_n}(0)=0$ y $F_{X_n}(1)=1$ para todo $n$. Calculemos $F_{X_n}(t)$ para $1/3 < t < 2/3$. El único modo de tener $X_n\le t$ para estos valores de $t$ es si $X_n\le 1/3$, lo cual sucede si el $n$-ésimo movimiento con popote fue desde el vaso de John hacia el vaso de Bill. Entonces, $F_{X_n}(t)=1/2$ para todo $n\ge 1$ si $1/3 < t < 2/3$.
Si $1/9< t < 2/9$ y $n\ge 2$, tenemos que $F_{X_n}(t)=P(X_n\le t)= P(X_n\le 1/9)$ es la probabilidad de que los primeros dos movimientos con popote fueron hacia el vaso de Bill; esta cantidad es igual a $1/4$. De modo similar, si $7/9 < t< 8/9$, tenemos que $F_{X_n}(t)=3/4$. De modo más general, recordemos la construcción del conjunto de Cantor. En cada paso $n$, borramos un tercio en el medio de cada intervalo producido en el paso $n-1$; y sobre cada uno de estos tercios, $F_{X_n}(t)$ es constante e igual al promedio de los valores de $F_{X_{n-1}}(t)$ sobre los intervalos adyacentes del paso $n-1$. En el límite, el resultado se llama “la escalera del diablo” de Cantor, y su gráfica se muestra abajo:
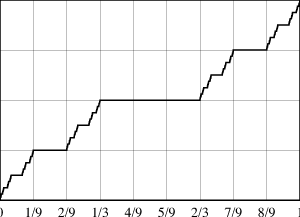
La escalera del diablo es una función continua y tiene la propiedad de que su derivada existe y es igual a cero fuera de un conjunto de longitud cero. La integral de Riemann de esta derivada de 0 a 1 no está definida, mientras la integral de Lebesgue está definida y es igual a cero, a pesar de que la función crece de 0 a 1 en este intervalo. Esta función muy interesante se introduce en cursos de análisis real de nivel posgrado como una fuente de contraejemplos, y es una sorpresa agradable observarla aparecer aquí como solución a nuestro problema.
Ya sabemos que \begin{equation} X_n=s^n x_0 + r\sum_{i=0}^{n-1} B_{n-i-1} s^i. \end{equation} Es intuitivamente claro (y, de hecho, fácil de demostrar) que, cuando $n$ tiende al infinito, el primer término se vuelve más y más pequeño, así que la condición inicial se vuelve menos y menos relevante. Podríamos decir, ingenuamente, que en el límite $n\to\infty$, $X_n$ debería tender a \begin{equation} r\sum_{i=0}^\infty B_{\infty-i-1} s^i. \end{equation} Por supuesto, esto no tiene sentido: $B_{\infty-i-1}$ no está descrito por ningún lanzamiento de moneda. Por otro lado, no hay diferencia entre dos lanzamientos de moneda: intercambiando el primer lanzamiento con el segundo, no cambiamos la distribución de probabilidad. Tal vez, entonces, se podría cambiar el orden de lanzamientos y preguntarse si $X_n$ tiende a la siguiente expresión: \begin{equation} Z=r\sum_{i=0}^\infty B_i s^i.\label{eqn:zdefine} \end{equation} Si le cuesta trabajo creer en este argumento, está en lo cierto. Después de todo, $X_n$ casi nunca converge mientras $Z$ siempre converge gracias al criterio de D'Alembert. Entonces, no hay modo para que $X_n$ converja a $Z$.
Y, sin embargo, como veremos en la siguiente sección, $X_n$ en realidad converge a $Z$, en el sentido de distribuciones de probabilidad. Es decir, para cada $a$ y $b$, $P(a\le X_n \le b)$ converge a $P(a\le Z\le b)$. Antes de explicar por qué se cumple esto, debemos decir algo sobre $Z$.
Resulta que $Z$ se conoce como una convolución de Bernoulli y se estudió por primera vez por Jessen y Wintner en 1935 [JW]B. Jessen, A. Wintner, Distribution functions and the Riemann zeta function. Trans. Amer. Math. soc. 38 (1935), 48—88.. El nombre es motivado por el efecto de la suma sobre variables aleatorias independientes. En $Z$ tenemos una cantidad infinita de variables aleatorias de Bernoulli $B_i$, cada una multiplicada por $s_i$ y todas sumadas. En general, si $X$ y $Y$ son variables aleatorias, la distribución de $X+Y$ se obtiene de la siguiente forma: para cada número real $z$, la probabilidad de que $X+Y$ sea igual a $z$ se obtiene sumando productos $P(X=x)P(Y=y)$ sobre todas las parejas de números $x$ y $y$ con $x+y=z$. Este tipo de operación se llama convolución y de aquí viene el término convolución de Bernoulli.
Las convoluciónes de Bernoulli son una familia de distribuciones muy notable. Tal vez, el lector ya percibió su naturaleza sorprendente al notar que la familia de distribuciones que da la respuesta al problema principal de este artículo debe contener todas las gráficas extrañas y picudas que ya vimos y que se interpolan entre la distribución normal y la uniforme. De hecho, la regularidad de $Z$ depende de $r$ en la manera que todavía no se entiende completamente, aún después de los trabajos de los gigantes como Erdős, y sigue siendo un área en desarrollo activo. Vamos a discutir esto en más detalle en la Sección 6.
Primero, demostraremos que la distribución de probabilidad de $X_n$ converge a la de $Z$.
Recordemos que: \begin{equation} X_n=s^n x_0 + r\sum_{i=0}^{n-1} B_{n-i-1} s^i. \end{equation} En esta sección, demostraremos que la distribución de probabilidad de $X_n$ converge a la distribución de probabilidad de \begin{equation} Z = r\sum_{i=0}^\infty B_i s^i. \end{equation} Primero, será muy útil saber que $F_Z(t)=P(Z\le t)$ es una función continua. En un momento, veremos que esto es lo mismo que decir que $Z$ no tiene parte discreta (es decir, $P(Z=t)=0$ para cada $t$). Es una consecuencia del trabajo de Jessen y Wintner (ver Teorema 11 en [JW]B. Jessen, A. Wintner, Distribution functions and the Riemann zeta function. Trans. Amer. Math. soc. 38 (1935), 48—88.); sin embargo, vale la pena saber que esto también se puede demostrar usando únicamente métodos elementales.
Demostración. Si $s$ y $t$ son dos números reales con $s< t$, entonces $Z\le s$ implica $Z\le t$ y $P(Z\le s) \le P(Z\le t)$, así que $F_Z(t)$ es una función no decreciente. También es intuitivamente claro (y se deriva directamente de los axiomas de la probabilidad) que si $T$ es un número real, el límite por la derecha $\lim_{t\to T^+} F_Z(t)$ existe y es igual a $P(Z\le T)$. Del mismo modo $\lim_{t\to T^-} F_Z(t)$ existe y es igual a $P(Z < T)$.
Entonces, para demostar que $F_Z(t)$ es continua, simplemente necesitamos ver que, para cada $T$, $P(Z=T)=0$. De aquí y hasta el final de esta demostración, $T$ será un número real fijo.
Para cada número natural $n$, sea $p_n$ la probabilidad de que, después de los primeros $n$ lanzamientos de moneda, todavía sea posible que $Z$ sea igual a $T$, dependiendo de los resultados de los lanzamientos futuros. Observemos que $p$ es una sucesión no creciente y que, para cada $n$, $P(Z=T)\le p_n$. Entonces, probaremos el teorema si demostramos que $\lim_{n\to\infty} p_n=0$.
Para cada $n$ sea $S_n$ el conjunto de sucesiones finitas $(b_0,\dots,b_{n-1})$ tales que existen $b_n, b_{n+1}, \dots$ con valores en $\{0,1\}$ con la propiedad de que $\sum_{i=0}^\infty b_i s^i=T$. Entonces, \[p_n = \frac{\#(S_n)}{2^n}\] donde $\#(\cdot)$ es la notación para el número de elementos en un conjunto.
Sea $N$ un número tal que $s^N < 1/2$ y sea $n$ un número natural.
Para cada sucesión finita $b=(b_0, b_1,\dots, b_{n-1})\in S_n$, definamos $U(b)\subset S_{n+N}$ como el conjunto de sucesiones que comienzan con $b$. Ahora, \[S_{n+N}= \bigcup_{b\in S_n} U(b),\] donde los conjuntos $U(b)$ en esta unión son disjuntos. Entonces, \[\#S_{n+N}=\sum_{b\in S_n} \#U(b).\] A priori, tenemos que $\#U(b)\le 2^N$. Veamos ahora que $\#U(b)\le 2^N-1$.
Extendamos cada sucesión finita $(b_0, b_1,\dots, b_{n-1})\in S_n$ a dos sucesiones de longitud $n+N$: $(c_0,\dots,c_{n+N-1})$ y $(d_0,\dots,d_{n+N-1})$, definidas de la siguiente manera: \[c_i= \begin{cases} b_i&\mbox{for $i< n$},\\ 0&\mbox{for $n\le i < n+N$} \end{cases} \] y \[d_i= \begin{cases} b_i&\mbox{for $i < n$},\\ 1&\mbox{for $n\le i < n+N$}. \end{cases}\] Por ejemplo, si $n=4$, $N=3$ y $b=(1,0,1,1)$, tenemos $c=(1,0,1,1,0,0,0)$ y $d=(1,0,1,1,1,1,1)$.
Ahora, demostremos que las sucesiones $c_i$ y $d_i$ no pueden estar en $S_{n+N}$ al mismo tiempo. Si $c_i$ y $d_i$ ambas están en $S_{n+N}$, debemos poder extenderlas a sucesiones infinitas $c_{N+n}, c_{N+n+1},\dots$ y $d_{N+n}, d_{N+n+1},\dots$ que toman sus valores in $\{0,1\}$ de tal forma que \[r\sum_{i=0}^\infty c_i s^i = T = r\sum_{i=0}^\infty d_i s^i.\] Por lo tanto, tenemos: \begin{eqnarray*} r\sum_{i=0}^{n-1}b_i s^i + r\sum_{i=n}^{n+N-1}0+ r\sum_{i=n+N}^\infty c_i s^i &=& r\sum_{i=0}^{n-1}b_i s^i + r\sum_{i=n}^{n+N-1}1s^i + r\sum_{i=n+N}^\infty d_i s^i\\ 0+r\sum_{i=n+N}^\infty (c_i-d_i) s^i &=& r\sum_{i=n}^{n+N-1}s^i\\ r\sum_{i=n+N}^\infty 1 s^i &\ge & r\sum_{i=n}^{n+N-1}s^i \\ s^{n+N}&\ge & s^n - s^{n+N}\\ 2s^N&\ge & 1\\ s^N&\ge & 1/2. \end{eqnarray*} Esto contradice el hecho de que $N$ fue escogido de tal manera que $s^N< 1/2$. Entonces, para cada sucesión $b$ in $S_n$, existe al menos una sucesión que comienza con $b$ y que no está en $U(b)$; lo que implica que $\# U(b)\le 2^N-1$.
Estamos listos ahora para dar una estimación para $p_n$. Tenemos \begin{eqnarray*} p_{n+N}&=&\frac{\# S_{n+N}}{2^{n+N}}\\ &=&\frac{\sum_{b\in S_n} \#U(b)}{2^{n+N}}\\ &\le&\frac{\#S_n (2^N-1)}{2^{n+N}}\\ &=&\frac{2^N-1}{2^N}\frac{\#S_n}{2^n}\\ p_{n+N}&\le&\frac{2^N-1}{2^N} p_n \end{eqnarray*} Por inducción, \[p_{kN}\le \left(1-\frac{1}{2^N}\right)^k p_0\] y tomando $k$ arbitrariamente grande, vemos que $\lim_{n\to \infty} p_n=0$.
Esto fue todo lo que necesitábamos para demostrar que $F_Z(t)$ es continua.
▢
Ahora tenemos todo para probar el resultado principal del presente artículo y relacionar $X_n$ con la convolución de Bernoulli $Z$.
Demostración. Primero consideremos la expresión para $X_n$: \[X_n = s^n x_0 + r\sum_{i=0}^{n-1} B_{n-i+1} s^i\] Para $n$ fijo, no hay diferencia entre los lanzamientos, y podemos permutar a los $B_i$ sin cambiar la distribución de probabilidad. Entonces, $X_n$ tiene la misma distribución de probabilidad (y, por lo tanto, la misma distribución cumulativa de probabilidad) que \[Y_n=s^n x_0 + r\sum_{i=0}^{n-1} B_i s^i\] o, dicho de otra forma, \[F_{X_n}(t) = F_{Y_n}(t).\] Mostremos ahora que $F_{Y_n}(t)$ converge a $F_Z(t)$.
Utilizando propiedades básicas de la serie geométrica, vemos que $Y_n$ y $Z$ tienen sus valores en el intervalo [0,1] y que, para todo $n$, \[0\le Z-r\sum_{i=0}^{n-1} B_i s^i\le s^n.\] Entonces, \[-s^n x_0 \le Z-Y_n \le s^n - s^n x_0\] lo que se puede escribir como \[Z-s^n +s^n x_0 \le Y_n\le Z+s^n x_0\] así que \[P(Z+s^n x_0 \le t) \le P(Y_n\le t) \le P(Z-s^n+s^n x_0\le t)\] o, en los términos de las funciones de distribución, \[F_Z(t-s^nx_0)\le F_{Y_n}(t)\le F_Z(t-s^nx_0+s^n).\] Por la continuidad de $F_Z$, cuando $n\to\infty$, ambos lados tienden a $F_Z(t)$; así $F_{Y_n}(t)=F_{X_n}(t)$ también tiene el mismo límite.
En los cursos introductorios de probabilidad usualmente se consideran dos clases de distribuciones de probabilidad: discretas y continuas (de hecho, absolutamente continuas). En realidad, hay más posibilidades y la convolución de Bernoulli puede proporcionar ejemplos de esto.
Una districbución discreta tiene soporte en un conjunto finito o numerable $A$ de los reales y es completamente determinada por los valores de $p(a)=P(X=a)$ para todos $a\in A$. En este caso, si $I$ es un sibconjunto de los reales, se cumple $P(X\in I)=\sum_{a\in I\cap A} p(a)$. Una variable aleatoria de Bernoulli es un ejemplo: aquí $A=\{0,1\}$. Si especificamos que $p(0)=p(1)=1/2$, obtenemos la distribución que describe una moneda honesta.
Por otro lado, una distribución absolutamente continua se describe por medio de una función de densidad de probabilidad $f(t)$ y la probabilidad se calcula con la fórmula $P(X\in [a,b])=\int_a^b f(t)\,dt$. La función cumulativa de la distribución es $F_X(t)=P(X\le t)=\int_{-\infty}^t f(t)\,dt$ y $F_X(t)=P(X\le t)=\int_{-\infty}^t f(t)\,dt$. Los ejemplos incluyen la distribución normal y la distribución uniforme.
No toda la distribución es discreta o absolutamente continua; por ejemplo, una distribución puede ser discreta en una región de la recta real y continua, en otra. Una situación más interesante es el caso de la convolución de Bernoulli con $r=2/3$, es decir, cuando $F_Z(t)$ es la escalera del diablo de Cantor como en la Figura 2. Si esta distribución fuera absolutamente continua, debería ser dada por una función de densidad $f(t)$ que es la derivada de $F_X(t)$. Sin embargo, en este caso, $f(t)$ es cero fuera de un conjunto de longitud cero. Sean los que sean los valores de $f(t)$ en ese conjunto, la integral de $f$ sobre el intervalo completo, o bien no está bien definida, o bien es cero; sin embargo, esta integral debería ser igual a 1 si el intervalo contiene todos los valores posibles de $Z$.
Por otro lado, $Z$ no es una distribución discreta: hemos visto en la demostración del Teorema 1 que, para todo $r$ y cualquer número real $t$, tenemos que $P(Z=t)=0$. Entonces, si $Z$ fuera una distribución discreta, su soporte sería vacio y, entonces, la probabilidad de $Z$ no estaría concentrada en ninguna parte, lo que es imposible. En el caso $r=2/3$, la distribución $Z$ no es, entonces, ni discreta ni absolutamente continua; llamaremos una distribución de este tipo puramente singular.
En general, una distribución de probabilidad se puede separar en una parte discreta, una parte absolutamente continua y una componente que se llama la parte singular. La parte singular tiene la misma propiedad que tiene la escalera del diablo: tiene $P(Z=t)=0$ en todos los puntos y $\frac{d}{dt} F(t)\,dt=0$, excepto en un conjunto de medida cero. Una distribución puramente singular tiene las partes discreta y absolutamente continua iguales a cero.
Se sabe desde los primeros estudios sobre las convoluciones de Bernoulli [JW]B. Jessen, A. Wintner, Distribution functions and the Riemann zeta function. Trans. Amer. Math. soc. 38 (1935), 48—88. que, para cada valor de $r$, la convolución de Bernoulli, o es absolutamente continua, o es puramente singular. Esto se debe a la existencia de una simetría que se puede describir como la ejecución de un movimiento con popote más, determinado por el lanzamiento de una moneda honesta. Esta simetría relaciona la distribución en partes diferentes del intervalo $[0,1]$ y, de hecho, puede ser utilizada para relacionar la distribución en todos los puntos de su soporte. Esto produce una autosimilitud que se puede usar para probar que cada parte del soporte de $Z$ tiene las mismas características de continuidad y regularidad que cualquiera otra parte.
Como hemos observado, para $r>1/2$, $Z$ es puramente singular (es la escalera del diablo), y para $r=1/2$, $Z$ es absolutamente continua (es la distribución uniforme); estos casos de la distribución de Bernoulli se habían entendido desde el principio. La situación para $r< 1/2$ es mucho menos clara. Se sabe que el conjunto de los $r$, para los cuales $Z$ es puramente singular, es infinito y que el conjunto de los $r$, para los cuales $Z$ es absolutamente continua, también es infinito. Vale la pena relatar algunos de los detalles de esta historia (nuestra fuente es [PSS]Y. Peres, W. Schlag, B. Solomyak, Sixty Years of Bernoulli Convolutions, Fractal Geometry and Stochastics, Progress in Probability 46 (2000), 39—65.).
En 1949, Erdős [E1]P. Erdős, On a family of symmetric Bernoulli convolutions, Amer. J. Math. 61 (1939), 974—975. demostró que, para $r< 1/2$, $Z$ es puramente singular cuando $\frac{1}{1-r}$ es un número de Pisot-Vijayaraghavan o, en breve, un número PV.
Un número PV es un número real $x>1$ que satisface una ecuación polinomial \[x^n+a_{n-1}x^{n-1}+\dots+a_0x^0=0\] con coeficientes enteros, y tal que las demás soluciones (reales y complejas) de esta ecuación tienen el módulo menor que 1. [Wiki] Pisot-Vijayaraghavan number, http://en.wikipedia.org/wiki/Pisot-Vijayaraghavan_number, [MW]D. Terr, E. W. Weisstein, Pisot Number. MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PisotNumber.html
Los números PV fueron descubiertos por C. Pisot [Pi]C. Pisot La répartition modulo 1 et les nombres algébriques, Annali di Pisa 7, 205—248, 1938. e, independientemente, por T. Vijayaraghavan [V]T. Vijayaraghavan, On the Fractional Parts of the Powers of a Number, II., Proc. Cambridge Phil. Soc. 37, 349—357, 1941., quien desarrollaba las ideas de G. H. Hardy relacionadas con las aproximaciones por números racionales. En efecto, los números PV tienen la propiedad de que sus potencias tienden a ser muy cercanas a los números enteros [Wiki] Pisot-Vijayaraghavan number, http://en.wikipedia.org/wiki/Pisot-Vijayaraghavan_number.
Estos números son relevantes en el contexto de algunos métodos para generar sucesiones de números seudoaleatorios en el intervalo $[0,1]$. Sucesiones de este tipo pueden aplicarse en las simulaciones por computadora (por ejemplo, en las simulaciones que utilizan el método Monte Carlo) y en los videojuegos para introducir lo que puede percibirse como azar. Uno de los métodos para manufacturar números seudoaleatorios consiste en escoger números reales positivos $\alpha, \theta$ y considerar la parte fraccionaria de $\alpha\theta^n$ para valores sucesivos de $n$. Sucesiones de este tipo suelen parecer aleatorias, al ser los valores sucesivos independientes y distribuirse uniformemente en el intervalo $[0,1)$.
Sin embargo, cuando $\theta$ es un número PV, esta sucesión tiende a converger a un número finito de puntos límite. Entonces, al diseñar un generador de números seudoaleatorios de este tipo, uno debe asegurarse de no elegir un número PV como $\theta$ ya que, en el caso contrario, la sucesión resultante no se verá “aleatoria”. (Las condiciones para que la parte fraccionaria de $\alpha\theta^n$ sea distribuida uniformemente no se conocen en general. Sin embargo, cuando $\theta$ es un número algebraico, la propiedad de $\theta$ de ser un número PV es equivalente a la existencia de un $\alpha\not=0$ tal que $\alpha\theta^n$ converge a un número finito de puntos límite [BDGPS]M.J. Bertin, A. Decomps-Guilloux, M. Grandet-Hugot; M. Pathiaux-Delefosse, and J.P. Schreiber, Pisot and Salem Numbers. Basel: Birkhäuser, 1992..)
La razón áurea $\phi=\frac{1+\sqrt{5}}{2}\cong 1.618033$ es un ejemplo de un número PV. Satisface $x^2-x-1=0$, y la única otra raíz, $0.618033$, tiene valor absoluto menor que 1. Resulta que $\phi^n$, para $n$ grande, es muy cercano a un entero.
Para ver esto, recordemos la sucesión de Fibonacci, definida por la relación de recurrencia: \begin{equation} F_{n+2}=F_{n+1}+F_n \label{eqn:fibo} \end{equation} con $F_0=0$, $F_1=1$. Algunos lectores probablemente saben que la relación de recurrencia (\ref{eqn:fibo}) tiene soluciones de la forma $F_n=u^n$ siempre y cuando $u$ satisfaga la ecuación polinomial: \[u^2=u+1.\] En este caso, una raíz ($\frac{1+\sqrt{5}}{2}$) es mayor que 1 y la otra ($\frac{1-\sqrt{5}}{2}$) está entre $-1$ y $0$. Por la linealidad, y con las condiciones iniciales $F_0=0$ and $F_1=1$, la fórmula para el $n$-ésimo número de Fibonacci es: \[F_n = \frac{1}{\sqrt{5}}\left(\frac{1+\sqrt{5}}{2}\right)^n - \frac{1}{\sqrt{5}}\left(\frac{1-\sqrt{5}}{2}\right)^n.\]
De hecho, la sucesión más relevante en nuestra situación es la de Lucas, con la misma relación de recurrencia $L_{n+2}=L_{n+1}+L_n$, pero con las condiciones iniciales $L_0=2$, $L_1=1$. Tenemos que: \[L_n = \left(\frac{1+\sqrt{5}}{2}\right)^n + \left(\frac{1-\sqrt{5}}{2}\right)^n.\] En efecto, esta expresión satisface $L_0=2$, $L_1=1$ y $L_{n+2}=L_{n+1}+L_n$. Por inducción, $L_n$ siempre es un entero; entonces, la distancia entre $\phi^n$ y un entero es \[\left(\frac{1-\sqrt{5}}{2}\right)^n\] y es cercana a cero para valores grandes de $n$.
Por lo tanto, la parte fraccionaria de $\phi^n$, o es muy pequeña, o cercana a 1. Por ejemplo, tenemos la siguiente tabla:
| $n$ | $\phi^n$ |
| 5 | 11.09017 |
| 10 | 122.99187 |
| 15 | 1364.000733 |
| 20 | 15126.99994 |
| 25 | 167761.000006 |
En general, como ya hemos mencionado, para cualquier número PV $\theta$, existe $\alpha>0$ tal que la parte fraccionaria de $\alpha\theta^n$ tiene un número finito de puntos límite. Esta propiedad de los números PV fue la que causó el interés inicial en ellos.
Aquí, sin embargo, nos interesa, sobre todo, el teorema de Erdős que afirma que, para $r=1-\frac{1}{\theta}$, con $\theta$ un número PV, la distribución $Z$ es singular. En el caso de la razón áurea, es decir, $r=1-\frac{1}{\phi}\cong 0.38166$, tenemos la siguiente ilustración generada numéricamente:
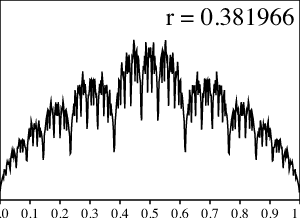
No obstante, hay que recordar que, en la situación en que la función es puramente singular debemos esperar que los métodos numéricos sean muy poco confiables y no produzcan los valores actuales. Lo dentada de la gráfica, probablemente, sea una buena indicación del hecho de que la función de densidad actual es muy dentada. Además, las áreas bajo la curva sobre cada intervalo $[a,b]$ deben ser aproximaciones decentes de las áreas correctas; sin embargo, se sabe que los picos de la gráfica, en realidad, van al infinito en un subconjunto denso, y esto no puede reflejarse plenamente en la imagen.
El número PV más pequeño (que produce el menor valor de $r$) es la raíz positiva de $x^3-x-1=0$, y $\frac{1}{1-r}\cong 1.324718$ (lo que se conoce como la “razón plateada”), dando $r\cong 0.245122$. [Wiki] Pisot-Vijayaraghavan number, http://en.wikipedia.org/wiki/Pisot-Vijayaraghavan_number, [MW]D. Terr, E. W. Weisstein, Pisot Number. MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PisotNumber.html. La convolución de Bernoulli $Z$, en este caso, se ve de la siguente forma:
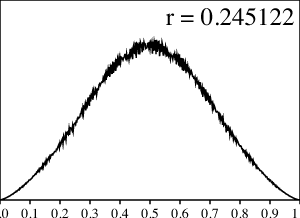
Observemos la notable semejanza que tiene esta gráfica con la distribución normal; la borrosidad, sin embargo, sugiere que la curva no es suave. De hecho, igual que en el caso de la razón aurea, el resultado de Erdős implica que esta borrosidad consiste en picos que, en realidad, se extienden al infinito.
¿Cuántos números PV existen? Lo que es más importante para nosotros ¿cuántos números PV hay de la forma $\frac{1}{1-r}$ con $0< r < 1/2$? Estos números son los que satisfacen $1<\frac{1}{1-r}< 2$ y, entonces, nuestra pregunta es equivalente al preguntar cúantos números PV existen en el intervalo $(1,2)$. Resulta que son una cantidad infinita, pero numerable.
El hecho de que esta cantidad sea numerable es la consecuencia de la definición: cada número PV viene de un polinomio con coeficientes enteros y sólo hay una cantidad numerable de éstos. El hecho de que es infinita se establece al producir explícitamente sucesiones infinitas de números PV en el intervalo $(1,2)$. Por ejemplo, consideremos la sucesión de polinomios: \[P_n(x)=1-x^2+x^n(1+x-x^2)\] con $n\ge 1$. Para cada $P_n$ sea $\theta_n$ la raíz real más grande de $P_n$; entonces $\theta_n>1$ es un número PV. Observemos que, para $n=1$, $\theta_1$ es la razón plateada y $\theta_n$ es una sucesión creciente de números PV que converge a la razón áurea: \[1.324718\cong \theta_1 < \theta_2 < \dots < \frac{1+\sqrt{5}}{2}\cong 1.618034\]
En 1940, Vijayaraghavan demostró que, además de la razón áurea, el conjunto de los números PV tiene un número infinito de puntos de concentración [V]T. Vijayaraghavan, On the Fractional Parts of the Powers of a Number, II., Proc. Cambridge Phil. Soc. 37, 349—357, 1941.. Un resumen detallado de lo que se sabe de los números PV menores de 2, incluyendo la descripción de todos los números PV menores que la razón áurea, se puede encontrar en [BDGPS]M.J. Bertin, A. Decomps-Guilloux, M. Grandet-Hugot; M. Pathiaux-Delefosse, and J.P. Schreiber, Pisot and Salem Numbers. Basel: Birkhäuser, 1992..
En la otra dirección, Erdős también demostró que hay un número positivo $a$ tal que el conjunto de los $r$, menores que $a$ y para los cuales $Z$ es puramente singular, tiene la medida de Lebesgue cero [E2]P. Erdős, On the smoothness properties of Bernoulli convolutions, Amer. J. Math. 62 (1940), 180—186.. En resumen, Erdős demostró que hay un número infinito de $r< 1/2$ para los cuales $Z$ es puramente singular, y un número infinito de $r< 1/2$ para los cuales $Z$ es absolutamente continua.
Es todo lo que Erdős dice sobre el asunto. Es difícil de imaginar que Erdős, quien insistía con tenacidad en la belleza en las matemáticas, estuviera satisfecho con esto y sospecho que la única razón por la cual no escribió más sobre el tema fue por que se quedó trabado.
El trabajo de Y. Peres y B. Solomyak en los 1990 fortalecieron el resultado de Erdős y demostraron que, para todo $r< 1/2$, salvo un subconjunto de medida de Lebesgue cero, $Z$ es absolutamente continua. Es decir, en lugar de afirmar la existencia de $a$, demuestran el teorema de Erdős con $a=1/2$.
Actualmente, los únicos casos conocidos de $r< 1/2$ para los cuales $Z$ es puramente singular son los que descubrió Erdős: son los que se obtienen al tomar $r=1-\frac{1}{\theta}$ donde $\theta$ es un número PV. No se sabe si existen otros ejemplos.
El comportamiento de $Z$ cuando $r$ tiende a $0$ es interesante y sutil. Hemos observado que la distribución, en este caso, tiene el aspecto de la distribución normal. Literalmente, esto no puede ser cierto, ya que $Z$ debe tener el soporte en $[0,1]$ y la distribución normal tiene el soporte sobre la recta real. No obstante, veremos que tiene sentido hablar de la convergencia de $Z$ a la distribución normal.
Recordemos que una distribución normal se caracteriza por el valor esperado y la varianza, así que será de utilidad calcular el valor esperado y la varianza para $Z$.
Denotemos el valor esperado por $E[\cdot]$ y la varianza por $Var(\cdot)$. Los siguientes hechos son estándares en cualquier texto de probabilidad para estudiantes de licenciatura (por ejemplo, [R]S. Ross, A First Course in Probability. 7 ed., Prentice Hall, 2005.). Sean $X$ y $Y$ dos variables aleatorias con valor esperado y varianza finitos, y sea $a$ una constante. Entonces, \begin{eqnarray*} E[X+Y]&=&E[X]+E[Y]\\ E[aX]&=&aE[X]\\ Var(aX)&=&a^2 Var(X). \end{eqnarray*} Si, además, $X$ y $Y$ son independientes, se cumple que: \begin{eqnarray*} E[XY]&=&E[X]E[Y]\\ Var(X+Y)&=&Var(X)+Var(Y) \end{eqnarray*}
Primero, la distribución de probabilidad de $Z$ es simétrica con respecto a la recta $x=1/2$. Esto corresponde a la idea de intercambiar los vasos de John y de Bill. No es sorprendente, entonces, que el valor esperado de $Z$ es $1/2$. Esto, también, se puede calcular directamente desde (\ref{eqn:zdefine}) usando las propiedades mencionadas del valor esperado y el hecho de que $E[B_n]=\frac{1}{2}$ para todo $n$.
De mismo modo, podemos calcular directamente $Var(B_n)=\frac{1}{4}$ y lo anterior se puede aplicar en (\ref{eqn:zdefine}) para obtener la varianza de $Z$ de la siguiente manera: \begin{eqnarray*} Var(Z)&=&Var\left(r\sum_{n=0}^\infty B_n s^n\right)\\ &=&r^2 Var\left(\sum_{n=0}^\infty B_n s^n\right)\\ &=&r^2 \sum_{n=0}^\infty \frac{1}{4} s^{2n}\\ &=&\frac{r}{4(2-r)} \end{eqnarray*}
Observemos que $\lim_{r\to 0} Var(Z)=0$. Entonces, cuando $r$ es muy pequeño, la mayor parte de la distribución de probabilidad está concentrada cerca de $1/2$. Si la distribución de probabilidad de $Z$ converge a la distribución normal cuando $r\to 0$, debe ser una distribución normal con varianza $0$; es decir, no es una distribución normal, sino la constante $Z=1/2$. Así tenemos otra evidencia de que el límite $t\to 0$ de $Z$ no puede ser una distribución normal.
Notemos que, cuando $r$ es, en realidad, igual a cero, hemos visto que el nivel de agua en el vaso de John permanece constante. Esto concuerda con el límite $r\to 0$ sólo si decidimos el nivel de agua en ambos vasos en la posición inicial esté a la mitad.
Un modo de pensar en el caso $r\to 0$ en términos de popotes y vasos de agua es tomar un intervalo pequeño de tiempo $\Delta t$ y declarar que un movimiento con popote aleatorio se ejecuta cuando el tiempo es un múltiplo de $\Delta t$. Tomemos el límite cuando $r$ y $\Delta t$ tienden a cero, de modo que $r=k\Delta t$. Entonces, habrá un flujo que la mitad del tiempo resultará en $\Delta x = -rx = -kx\Delta t$, y la otra mitad en $\Delta x = r(1-x) = k(1-x)\Delta t$. Cuando observamos este proceso para los valores macroscópicos de $t$, la ley de los grandes números sugiere que debemos usar la ecuación diferencial: \[\frac{dx}{dt}= \frac{1}{2}(-kx) + \frac{1}{2}(k(1-x))\] o, simplificando: \[\frac{dx}{dt} = -kx + \frac{k}{2}.\] La solución se obtiene con métodos estándares, y es: \[x=(x_0-1/2) e^{-kt} + \frac{1}{2}\] Entonces, cuando $t$ va al infinito (lo que correponde a $n\to \infty$), $x$ converge a $1/2$.
¿Qué sucede si cambiamos la escala para que el valor esperado de $Z$ sea 0 y la desviación estándar (y, entonces, la varianza) sea igual a 1? Definamos: \begin{equation} V=\frac{Z-E[Z]}{\sqrt{Var(Z)}} = \frac{2\sqrt{2-r}}{\sqrt{r}} (Z-1/2). \label{eqn:definev} \end{equation} Resulta que, cuando $r\to 0$, la distribución de probabilidad de $V$ converge a la distribución normal con el valor esperado 0 y la desviación estándar 1 [JW]B. Jessen, A. Wintner, Distribution functions and the Riemann zeta function. Trans. Amer. Math. soc. 38 (1935), 48—88. (una distribución normal con el valor esperado 0 y la desviación estándar 1 se llama un distribución normal estándar). Éste es el significado real de la afirmación que, mientras $r\to 0$, $Z$ se aproxima a la distribución normal. La demostración involucra funciones generadoras de momentos; la esbozamos brevemente a continuación.
Los momentos de una variable aleatoria $V$ son los números $\mu_k=E[V^k]$ para todos los enteros no negativos $k$. Siempre tenemos $\mu_0=1$, y $\mu_1$ es el valor esperado de $V$. En muchos casos, la sucesión de los momentos determina la distribución. Podemos juntar estos números en una función generadora de momentos: \[M_V(t)=\sum_{k=0}^\infty \frac{\mu_k}{k!}t^k=E\left[e^{tV}\right].\]
Si consideramos $V$ como en (\ref{eqn:definev}), la función generadora de momentos para $V$ será: \[M_V(t)=E\left[e^{t\frac{2(2-r)}{\sqrt{r}}r\sum_{n=0}^\infty (B_n-\frac{1}{2})s^n}\right].\] El lector puede verificar que esto se simplifica a: \[M_V(t)=\prod_{n=0}^\infty \cosh (t\sqrt{2-r}\sqrt{r}s^n).\] Expandiendo $\log M_V(t)$ en una serie de potencias alrededor de $t=0$, encontramos que, cuando $r\to 0$, la serie de potenicas para $\log M_V(t)$ converge, término por término, a $t^2/2$. Entonces, la serie de Taylor para la función generadora de momentos $M_V(t)$ converge, término por término, a la serie para $e^{t^2/2}$, la cual es la función generadora de momentos para la distribución normal. De hecho, solamente la distribución normal estándar tiene esta función generadora de momentos, así que la distribución de $V$ converge a la distribución normal estándar.
También es interesante ver como este hecho se relaciona con el teorema central del límite, la cual es uno de los teoremas principales de la teoría de probabilidad. La historia del teorema central del límite es la siguiente. El promedio de variables aleatorias de Bernoulli independientes \[W_n=\frac{B_0+\dots+B_{n-1}}{n}\] comparte ciertos rasgos con con la convolución de Bernoulli $Z$: ambas toman valores en $[0,1]$ y, cuando $n$ crece, la distribución de $W_n$ converge a la constante $1/2$, lo que se puede ver observando que $E[W_n]=1/2$ y $Var(W_n)=\frac{1}{4n}$. Si cambiamos la escala de $W_n$ para mantener el valor esperado constante en $0$ y la varianza en $1$ de la siguinete manera: \[2\sqrt{n}\left(W_n-\frac{1}{2}\right),\] entonces, el resultado converge a la distribución normal estándar. Observemos la relación entre $W_n$ y $Z$. Cuando $r$ tiende a $0$, $s$ tiende a $1$, y $Z$ se ve como un múltiplo de la simple suma de las $B_i$. Por supuesto, la suma de las $B_i$ casi siempre diverge, pero tanto en el caso de $W_n$ como en el caso de $Z$, esta suma se multiplica por algo cercano a cero. Para $W_n$, este factor es $1/n$; para $Z$, es $r$. Esto, sin embargo, no es suficiente: como sólo multiplicamos por este factor al final, necesitamos reducir los términos individuales. Para $W_n$, multiplicamos todos los términos arriba de $n$ por cero; para $Z$, multiplicamos cada término por una potencia de $s$ que haga que los términos con $n$ grande sean menos relevantes.
Esto no es una demostración de que $V$ converge a la distribución normal pero, al menos, hemos conectado este hecho (mediante una analogía, en todo caso) con la intuición que proviene del teorema central del límite (Yuval Peres me informó de un argumento riguroso, el cual salió de las discusiones entre él y Yoav Freund; consiste en aplicar la versión de Lindeberg del teorema central del límite a sumas truncadas, donde los términos truncados dependen de $r$. A saber, si se truncan los términos despues del número $N$ lo suficientemente grande para que $s^N< r^2$, las condiciones para el teorema central del límite de Lindeberg se cumplen. Las series truncadas se aproximan a la serie infinita completa y la diferencia converge a cero uniformemente. [YP]Yuval Peres, comunicación personal, 12 de marzo, 2007..)
En conclusión, si $X_n$ es la cantidad de agua en el vaso de John después de $n$ movimientos con popote aleatorios, $X_n$ casi nunca converge, pero la distribución de probabilidad de $X_n$ converge a la de la convolución de Bernoulli $Z$. Las propiedades de $Z$ son:
Quisiera agradecer a mi colega Prof. Kendra Killpatrick por contarme este problema. También, agradezco al Prof. Chris Hoffman, de la Universidad de Washington, por quien me enteré sobre el trabajo de Peres y Solomyak y, por lo tanto, aprendí sobre el tema de las convoluciones de Bernoulli.
El algoritmo para hacer la las ilustraciones funciona de la siguiente manera. Primero, definimos la variable MAXLEVEL que determina cuantos moviemientos de popote se hacen. Después, dividimos el intervalo unitario en subintervalos iguales (llamados compartimientos) para recordar los datos. Después, para cada sucesión posible de MAXLEVEL lanzamientos de la moneda con el valor inicial $x_0=0$, recordamos el compartimiento donde llegamos al final. La probabilidad que asignamos el compartimiento al final es el número de veces que llegamos ahí dividido por $2^{\tt MAXLEVEL}$.
A continuación, damos el seudocódicgo para este cálculo. El programa actual está escrito en C y produce las ilustraciones (en particular, las de este artículo) en postscript encapsulado.
Observemos que el algoritmo asume que $x_0=0$, lo que es un extremo. La precisión de parar la simulación después de MAXLEVEL iteraciones se puede juzgar comparando los resultados con otros valores de $x_0$. El caso $x_0=1$ producirá dibujos similares aunque reflejados alrededor de la recta $x=1/2$; por lo tanto, la presencia de la simetría con respecto a esta recta es una indicación de que MAXLEVEL es lo suficiente grande. Por ejemplo, si el lector intenta esta simulación para $r< 0.03$, notará la asimetría; esto significa que MAXLEVEL debe escogerse más grande, aunque el tiempo necesario para terminar el programa se duplica para cada incremento a MAXLEVEL.
BINS = 500
MAXLEVEL = 20
int tally[BINS]; /* The data */
/* Do straw move, recursively */
/* depth = current depth, */
/* x = current amt of water in glass, */
/* r = fraction of glass in straw*/
Procedure strawmove(depth, x, r)
Start;
if ( depth >= MAXLEVEL ) {
increment tally[ floor(r*BINS) ];
}
else {
strawmove(depth+1,x*(1-r),r);
strawmove(depth+1,x*(1-r)+r,r);
}
End.
Main Program: /*The main program */
Start;
x0 = 0.0; /* The initial value x0: John's glass starts empty */
print("Enter a value for r: ");
input r; /* Ask the user to provide a value for r */
clear_array tally[];
strawmove(0,x0,r); /* Do the recursive computation */
/* Print out results */
for (i=0;i< BINS;i++)
print (i/BINS, tally[i]/2^MAXLEVEL);
End.
[BDGPS] M.J. Bertin, A. Decomps-Guilloux, M. Grandet-Hugot; M. Pathiaux-Delefosse, and J.P. Schreiber, Pisot and Salem Numbers. Basel: Birkhäuser, 1992.
[E1] P. Erdős, On a family of symmetric Bernoulli convolutions, Amer. J. Math. 61 (1939), 974—975.
[E2] P. Erdős, On the smoothness properties of Bernoulli convolutions, Amer. J. Math. 62 (1940), 180—186.
[IK] K. Iga, K. Killpatrick, Truck drivers, a straw, and sharing a glass of water, College Mathematics Journal 37 (2006), no. 2, 82—92.
[I2] K. Iga, The truck driver's straw problem and Cantor sets. College Mathematics Journal 39 (2008), no. 4, 280—290.
[JW] B. Jessen, A. Wintner, Distribution functions and the Riemann zeta function. Trans. Amer. Math. soc. 38 (1935), 48—88.
[PS] Y. Peres, B. Solomyak, Absolute continuity of Bernoulli convolutions, a simple proof., Math Research Letters 3 (1996), no. 2, 231—239.
[PSS] Y. Peres, W. Schlag, B. Solomyak, Sixty Years of Bernoulli Convolutions, Fractal Geometry and Stochastics, Progress in Probability 46 (2000), 39—65.
[Pi] C. Pisot La répartition modulo 1 et les nombres algébriques, Annali di Pisa 7, 205—248, 1938.
[R] S. Ross, A First Course in Probability. 7 ed., Prentice Hall, 2005.
[V] T. Vijayaraghavan, On the Fractional Parts of the Powers of a Number, II., Proc. Cambridge Phil. Soc. 37, 349—357, 1941.
[Wiki] Pisot-Vijayaraghavan number, http://en.wikipedia.org/wiki/Pisot-Vijayaraghavan_number.
[MW] D. Terr, E. W. Weisstein, Pisot Number. MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/PisotNumber.html
[YP] Yuval Peres, comunicación personal, 12 de marzo, 2007.

Nací el 19 de octubre de 1970 en Honolulu, Hawaii, estudié en la Moanalua High School en 1984-1988, obtuve mi licenciatura en matemáticas y física en MIT en 1992 y recibí mi doctorado en matemáticas en la Universidad de Stanford en 1998.
Soy profesor asociado en matemáticas en la Universidad de Pepperdine, un four-year liberal arts college en Malibú, California. Mi trabajo involucra 12 horas de docencia por semana, es decir, 3 cursos cada semestre, e investigación. La lista de los cursos que doy puede ser consultada en mi página; mi investigación se concentra en el área de topología que estudia variedades de dimensión 4 usando las ecuaciones de Seiberg-Witten y otros métodos relacionados.
Mis otros intereses incluyen geometría diferencial, teoría de Morse, supersimetría y (cambiando de tema) la crítica de textos Bíblicos. En general, trabajo en cualquer problema de matemáticas que cruce mi camino y que me parezca divertido.
Estoy involucrado en la Iglesia Presbiteriana de Malibú, y como alumnus en Alpha Phi Omega, una fraternidad nacional de servicio en EU.