

Probablemente, los problemas más interesantes de las olimpiadas matemáticas son aquellos que, detrás del lenguaje elemental, esconden una trama del mundo de las matemáticas más profundas. Con este artículo, inauguramos una serie de textos dedicados a problemas de este tipo.
Comenzamos con un problema de geometría combinatoria que apareció en la Olimpiada Matemática de los Estados Unidos de America en 2014.
Una solución posible empieza con la traslación $x\mapsto x-671$ para transformar la condición de colinealidad en \begin{eqnarray*} a+b+c=1. \end{eqnarray*} Esto simplificará los cálculos en lo que sigue.
Es natural buscar un modelo polinomial $(p(x),q(x))$ para las coordenadas de los puntos. La condición de colinealidad, traducida en coordenadas, es \begin{eqnarray*} \left|\begin{array}{ccc} p(a) & q(a) & 1\\ p(b) & q(b) & 1\\ p(c)& q(c)& 1 \end{array} \right|=0, \end{eqnarray*} o, en otras palabras, \begin{eqnarray*} p(a)q(b)+p(b)q(c)+p(c)q(a)-p(a)q(c)-p(b)q(a)-p(c)q(b)=0. \end{eqnarray*} Esto debería ocurrir si y sólo si $a+b+c=1$ o si dos de los números $a,b,c$ son iguales. Entonces, el lado izquierdo de la ecuación, que es un polinomio en los variables $a,b,c$, debe ser de la forma \begin{eqnarray*} (a+b+c-1)(b-a)(c-b)(a-c)R(a,b,c), \end{eqnarray*} donde $R(a,b,c)$ es un polinomio. Consideremos el caso más sencillo, \begin{eqnarray*} R(a,b,c)=1. \end{eqnarray*}
En este caso, los primeros coeficientes de $p(x)$ y $q(x)$ son iguales a $1$. Los polinomios $p(x)$ y $q(x)$ no pueden ser cuadráticos porque, en este caso, los términos de grado $4$ de la expresión \begin{eqnarray*} p(a)q(b)+p(b)q(c)+p(c)q(a)-p(a)q(c)-p(b)q(a)-p(c)q(b) \end{eqnarray*} se cancelan completamente y, sin embargo, la expresión \begin{eqnarray*} (a+b+c-1)(b-a)(c-b)(a-c) \end{eqnarray*} contiene términos de grado $4$. Entonces, uno de los polinomios $p(x)$ y $q(x)$ es cúbico, y el otro es lineal. Sea $p(x)$ el polinomio lineal. Con una traslación podemos trsansformar este polinomio en $p(x)=x$. Por lo tanto, debemos tener \begin{eqnarray}\label{firstequ} \begin{array}{rr}(c-b)Q(a)+(a-c)Q(b)+(b-a)Q(c)\\ =(a+b+c-1)(b-a)(c-b)(a-c). \end{array} \end{eqnarray} Escribiendo $Q(x)=x^3+\alpha x^2+\beta x+\gamma$, observamos que la parte lineal de $Q(x)$ se cancela en la ecuación (\ref{firstequ}), entonces podemos escoger $Q(x)=x^3+\alpha x^2$.
Sustituyendo $a=0,b=-1,c=1$ en (\ref{firstequ}), obtenemos \begin{eqnarray*} -2Q(0)-Q(-1)-Q(1)=2, \end{eqnarray*} entonces, $\alpha=-1$.
Volviendo al caso del problema con $2014$ en lugar de $1$, obtenemos la familia de puntos \begin{eqnarray*} P_n=(n-671,(n-671)^3-(n-671)^2). \end{eqnarray*} Pero, como lo explicamos antes, podemos reemplazar $n-671$ por $n$ e ignorar la parte lineal de $Q(x)$. De esta manera, obtenemos una fórmula más sencilla para una familia de puntos que satisface la condicion del problema: \begin{eqnarray*} P_n=(n,n^3-3\cdot 671n^2-n^2)=(n,n^3-2014n^2). \end{eqnarray*}
La solución produce un conjunto de puntos colocados en la curva cúbica \begin{eqnarray*} y=x^3-2014x. \end{eqnarray*} Esto no es un accidente. Como observaron algunos de los alumnos de la olimpiada, la mayoría de las curvas cúbicas contienen un conjunto de puntos con la propiedad deseada.
Después de la traslación de los índices \begin{eqnarray*} a\mapsto a-\frac{2014}{3}, b\mapsto b-\frac{2014}{3}, c\mapsto c-\frac{2014}{3}, \end{eqnarray*} la condición para que los puntos $P_a,P_b,P_c$ sean colineales se transforma en \begin{eqnarray*} a+b+c=0. \end{eqnarray*} Y esto se puede relacionar con una propriedad fundamental de una familia de curvas cúbicas, las curvas elípticas.
Una curva elíptica se define por una ecuación de forma \begin{eqnarray*} f(x,y)=0, \end{eqnarray*} donde $f(x,y)$ es un polinomio de grado $3$ en las variables $x,y$ con la propiedad que para ningún punto $(x_0,y_0)$ de la curva se cumple $$\frac{\partial f}{\partial x}(x_0,y_0)=\frac{\partial f}{\partial y}(x_0,y_0)=0.$$ Usando una transformacion de coordenadas, la equación de la curva se puede transformar en \begin{eqnarray*} y^2=x^3+ax+b,\quad a,b\in {\mathbb R}. \end{eqnarray*} Dependiendo de si la ecuación $x^3+ax+b=0$ tiene una raíz real o tres raíces reales, la curva elíptica tiene una componente o dos (Figura 1). Esta curva tiene una estructura de grupo abeliano, la cual explicaremos a continuación.
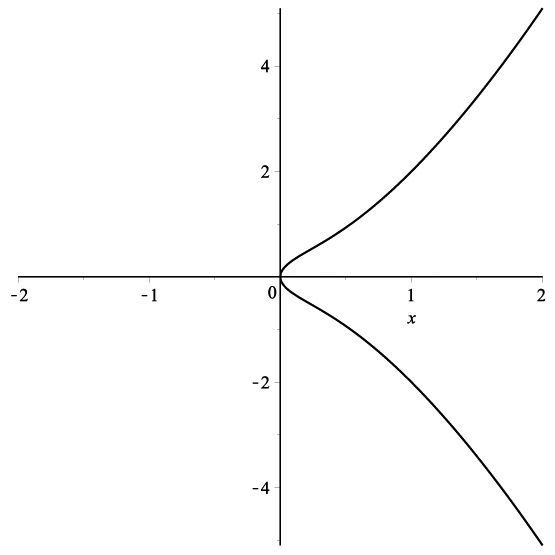
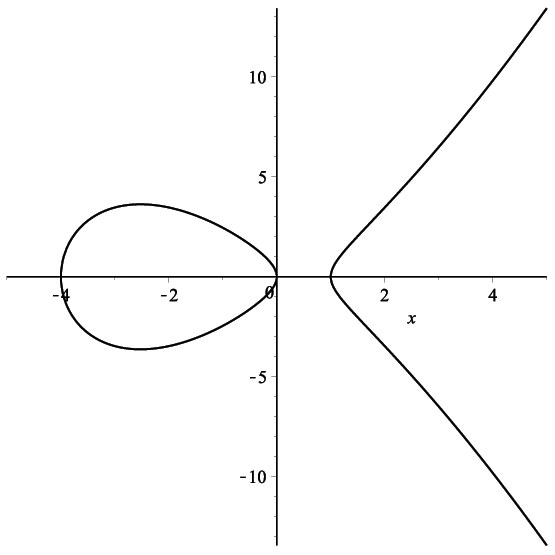
Para definir la suma de dos puntos $P$ y $Q$ en la curva, consideremos la recta que pasa por $P$ y $Q$. Sea $\alpha x+\beta y+\gamma=0$ la ecuación de esta recta. Las intersecciones de la recta con la curva elíptica se obtienen resolviendo el sistema de ecuaciones \begin{eqnarray*} &&y^2=x^3+ax+b\\ &&\alpha x+\beta y+\gamma=0. \end{eqnarray*} Sustituyendo $y=-(\alpha x+\gamma)/\beta $ en la primera ecuación obtenemos una ecuación cubica en $x$. Esta ecuación tiene dos soluciones reales (las coordenadas de $P$ y $Q$) y, por lo tanto, tiene otra solución real que nos da un otro punto de intersección de la recta con la curva. Denotemos este punto por $R$.
Esta construcción funciona bien si $\beta\neq 0$; pero si $\beta=0$, obtenemos la ecuación de la recta: $x=-\gamma/\alpha$; la recta es vertical. Esta recta cruza la curva elíptica sólo en dos puntos con las coordenadas \begin{eqnarray*} \left(-\gamma/\alpha, \pm \sqrt{(-\gamma/\alpha)^3+a(-\gamma/\alpha)+b}\right), \end{eqnarray*} y estos dos puntos son precisamente $P$ y $Q$.
Esta situación se puede arreglar si añadimos a la curva elíptica el punto en el infinito. Lo hacemos pasando al plano proyectivo, que es una extensión del plano euclidiano en la cual cada dos rectas se intersectan. En el plano proyectivo, cada recta tiene un punto en el infinito, y todos los puntos en el infinito se encuentran en la recta en el infinito. Dos rectas se intersectan en puntos finitos si no son paralelas, pero cuado son paralelas se intersectan en un punto en el infinito. Entonces un punto en el infinito es especificado por la dirección de las rectas paralelas que se intersectan en este punto. El punto en el infinito de la curva elíptica es el punto especificado por la dirección vertical. Por lo tanto, en el caso que la recta $PQ$ es vertical, podemos definir el punto $R$ como el punto en el infinito de esta recta.
Por motivos de álgebra, esta definición funciona bien; además, en el caso $P=Q$, es decir, cuando la recta $PQ$ es la recta tangente a la curva elíptica. También, si alguno de los puntos $P$ o $Q$ está en el infinito, la recta $PQ$ es vertical y, entonces, intersecta una vez más la curva elíptica; sea esta intersección el punto $R$ deseado. Finalmente, si $P$ y $Q$ coinciden con el punto en el infinito, definimos $R$ como el punto en el infinito.
Ahora podemos definir la estructura de grupo. Fijemos un punto $O$ en la curva elíptica. Como veremos en un momento, este punto será la identidad del grupo. Para definir $P+Q$, consideramos el punto $R$ asociado con estos dos puntos, y despues aplicamos el mismo procedimiento para construir el punto asociado con el par $(O,R)$. El punto que así obtenemos es $P+Q$. Para resumir, la suma $P+Q$ se obtiene intersectando la curva elíptica con la recta $PQ$, tomando el punto $R$ de intersección, y después intersectando la curva de nuevo con la recta $OR$ (Figura 2).
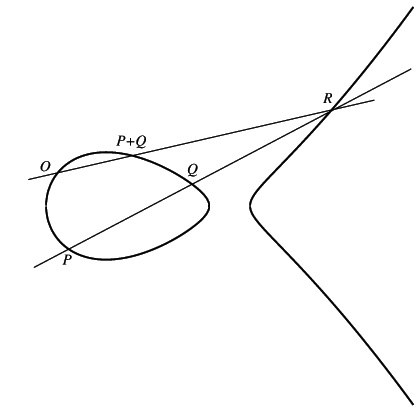
Esta construcción se vuelve más elegante en el caso de que $O$ es el punto en el infinito. En este caso, $P+Q$ es la reflexión de $R$ sobre la abscisa.
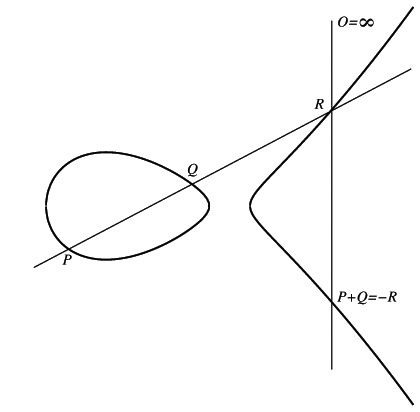
Se pueden verificar geométricamente las siguientes propiedades:
Observemos que tres puntos $P,Q,R$ en la curva son colineales si y sólo si \begin{eqnarray*} P+Q+R=0. \end{eqnarray*} Deducimos que el problema de olimpiadas está resuelto si el grupo asociado a la curva elíptica tiene un subgrupo isomorfo a ${\mathbb Z}$. Para comprobar esto, necesitamos entender mejor la estructura de este grupo.
Después de añadir el punto en el infinito, la curva consiste de una o dos componentes cerradas; salvo una deformación, cada componente es un círculo. En efecto, el punto en el infinito cierra la componente no acotada en un círculo: uno llega a este punto tanto por la rama infinita superior, como por la rama infinita inferior.
La operación de la suma del grupo asociado con la curva es una función continua de dos variables con valores en la curva, ya que no es difícil de verificar geométricamente que si $P'\rightarrow P$ y $Q'\rightarrow Q$, entonces $P'+Q'\rightarrow P+Q$. También, la función que asocia con un punto su inverso, $P\rightarrow -P$, es continua. Por lo tanto, estamos en la presencia de un grupo de Lie abeliano de dimensión 1, es decir, una curva con una estructura de grupo abeliano en cual la operación del grupo y la operación de tomar el inverso (negativo) son continuas.
En nuestro caso, el grupo de Lie tiene una o dos componentes que son curvas cerradas. Los grupos de Lie de este tipo son clasificados. En el caso de una componente, tenemos solamente el grupo de rotaciones del plano alrededor de un punto. Éste es el mismo que el grupo multiplicativo de los números complejos cuyo módulo es igual a $1$: \begin{eqnarray*} U(1)=\{z\in {\mathbb C}\,|\,|z|=1\}. \end{eqnarray*} Por el otro lado, si la curva tiene dos componentes, entonces, el grupo es \begin{eqnarray*} U(1)\times {\mathbb Z}/2{\mathbb Z}, \end{eqnarray*} con la suma definida separadamente en cada coordenada (aquí ${\mathbb Z}/2{\mathbb Z}$ es el grupo, con dos elementos, de las clases de residuos módulo 2). En ambos casos, el grupo contiene una copia de $U(1)$. El subgrupo \begin{eqnarray*} G_\theta=\{e^{n\theta i}\,|\, n\in {\mathbb Z}\} \end{eqnarray*} de las rotaciones por ángulos múltiplos de un ángulo $\theta$ con $\theta/\pi$ irracional es isomorfo a ${\mathbb Z}$ y resuelve el problema porque, si $P_n$ denota el punto asociado con el elemento $e^{n\theta i}$, entonces $P_k+P_m+P_n=0$ si y sólo si $k+m+n=0$.
Concluimos nuesta discusión con la observación de que el nombre de las curvas elípticas viene de las integrales elípticas, que son integrales de forma \begin{eqnarray*} \int R(x,y)dx \end{eqnarray*} donde $R$ es una función racional y $y=\sqrt{P(x)}$ con $P(x)$ un polinomio de grado $3$ o $4$ sin raíces dobles. Una de estas integrales calcula la longitud del arco de la elipse.
El lector de este artículo puede encontrar más información sobre curvas elípticas y su estructura de grupo en [1], sobre grupos de Lie en [2], y sobre integrales elípticas en [3].
[1] I.R. Shafarevich, Basic Algebraic Geometry 1: Varieties in Projective Space, Springer 1994.
[2] B.C. Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, 2004.
[3] C. Houzel, Fonctiones elliptiques et intégrales abéliennes in J. Dieudonné (ed.), Abregé d'Histoire des Mathématiques, Hermann, 1978, 1-114.
