

El presente artículo es de naturaleza puramente expositiva, y su objetivo central es discutir ciertas conexiones entre el análisis no arquimediano y la física de ciertos sistemas complejos. Las aplicaciones del análisis no arquimediano a la física están motivadas por dos ideas. La primera es la conjetura en física de partículas, propuesta por Igor Volovich, que afirma que, a nivel de la escala de Planck, el espacio-tiempo tiene una estructura no arquimediana. La segunda idea viene de la física estadística, más exactamente de modelos que describen la “relajación” en sistemas tales como macromoléculas y proteínas. La naturaleza no exponencial de tales relajaciones es explicada por los físicos al proponer que el comportamiento mostrado por estos sistemas se debe a que su espacio de estados tiene una estructura jerárquica. El presente artículo es un primer intento de explicación de las ideas antes mencionadas. El artículo se centra en las ecuaciones del calor $p$-ádicas y su conexión con modelos de sistemas complejos.
En esta sección fijamos la notación y presentamos algunos resultados básicos sobre el análisis $p$-ádico que serán utilizados a lo largo de este trabajo. Para una exposición más completa sobre el análisis $p$-ádico, el lector puede consultar [1]Albeverio S., Khrennikov A. Yu., Shelkovich V. M., Theory of p-adic distributions: linear and nonlinear models. Cambridge University Press, 2010., [8]Taibleson M. H., Fourier analysis on local fields, Princeton University Press, 1975., [9]Kochubei A.N., Pseudo-differential equations and stochastics over non-Archimedean fields. Marcel Dekker, Inc., New York, 2001., [17]Vladimirov V. S., Volovich I. V., Zelenov E. I., p-adic analysis and mathematical physics, World Scientific, 1994..
Una norma $\left\vert \cdot\right\vert $ sobre $\mathbb{Q}$ es una función real valuada que satisface las siguientes propiedades:
Una pregunta natural es la siguiente: ¿qué normas existen en $\mathbb{Q}$? La respuesta la da el siguiente resultado; ver por ejemplo [1]Albeverio S., Khrennikov A. Yu., Shelkovich V. M., Theory of p-adic distributions: linear and nonlinear models. Cambridge University Press, 2010..
Las normas $p$-ádicas se definen de la siguiente forma. Fijemos un primo $p$ y sea $x\in\mathbb{Q\smallsetminus}\left\{ 0\right\} $. Así, $x$ se expresa de forma única como $x=p^{v}\cdot\frac{a}{b}$, donde $v$ es un entero y $a$, $b$ son números enteros relativamente primos con $p$. Podemos, entonces, definir \[ \left\vert x\right\vert _{p}=p^{-v}, \] donde el entero $v=v\left( x\right) $ se denomina el orden $p$-ádico de $x$ y será denotado por $ord\left( x\right) $. Por definición $|0|_p=0$, y $ord(0)=+\infty $. La norma $\left\vert \cdot\right\vert _{p}$ satisface (1), (2), pero la propiedad (3) tiene una forma más fuerte: \[ 3^{\prime}.\text{ }\left\vert x+y\right\vert _{p}\leq\max\left\{ \left\vert x\right\vert _{p},\left\vert y\right\vert _{p}\right\}. \] Cuando una norma satisface la propiedad $3^{\prime}$ se dice no arquimediana.
Podemos ahora definir una distancia sobre $\mathbb{Q}$ tomando $d(x,y):=\left\vert x-y\right\vert _{p}$. Así $\left( \mathbb{Q},d\right) $ es un espacio métrico. La completación de $\mathbb{Q}$ con respecto a $\left\vert \cdot\right\vert _{p}$ se obtiene adjuntado a $\mathbb{Q}$ los límites de las secuencias de Cauchy con respecto a $\left\vert \cdot\right\vert _{p}$. La completación de $\mathbb{Q}$ con respecto al valor absoluto usual conduce a $\mathbb{R}$ y la completación de $\mathbb{Q}$ con respecto a $\left\vert \cdot\right\vert _{p}$ conduce al cuerpo de los números $p$-ádicos $\mathbb{Q}_{p}$.
Todo número $p$-ádico puede ser representado como una serie de la forma \begin{equation} x=p^{v} \sum\limits_{i=0}^{\infty} x_{i}p^{i},\text{ con }x_{i}\in\left\{ 0,1,\cdots,p-1\right\} \, \text{y}\, x_0 \, \neq 0; \label{eq1A} \end{equation} esta serie converge en la norma $\left\vert \cdot\right\vert _{p}$. La representación (\ref{eq1A}) se puede interpretar diciendo que un número $p$-ádico $x$ es el límite, en la norma $|\cdot|_{p}$, de la sucesión \[ x^{(m)}=p^{v}(x_{0}+x_{1}p+\cdots+x_{m}p^{m})\in\mathbb{Q}. \] La parte fraccionaria de $x\in\mathbb{Q}_{p}$, denotada como $\left\{ x\right\} _{p}$, es el siguiente número racional: \[ \left\{ x\right\} _{p}:=\left\{ \begin{array} [c]{llll} 0 & \text{si} & x=0\text{,} & \text{ó}\, \, \, \, ord(x)\geq0\\ p^{v} \sum\limits_{j=0}^{\left\vert v\right\vert -1} x_{j}p^{j} & \text{si} & ord(x)< 0. & \end{array} \right. \]
La bola unitaria \[ \mathbb{Z}_{p} =\{x\in\mathbb{Q}_{p}:|x|_{p}\leq1\}=\{x\in\mathbb{Q}_{p}:x=\sum_{i=i_{0}}^{\infty}x_{i}p^{i},i_{0}\geq0\}, \] es un dominio de ideales principales. Más exactamente, cualquier ideal de $\mathbb{Z}_{p}$ tiene la forma \[ p^{m}\mathbb{Z}_{p}=\{x\in\mathbb{Z}_{p}:x=\sum_{i\geq m}a_{i}p^{i} \},\ m\in\mathbb{N}. \]
Desde el punto de vista geométrico, los ideales de la forma $p^{m} \mathbb{Z}_{p},\ m\in\mathbb{Z}$, forman un sistema fundamental de vecindades del origen en $\mathbb{Q}_{p}$.
La norma $p$-ádica puede extenderse al espacio $n$ dimensional $\mathbb{Q}^n_{p}$ tomando \[ ||x||_{p}:=\max_{1\leq i\leq n}|x_{i}|_{p},\qquad\text{para }x=(x_{1},\dots,x_{n})\in\mathbb{Q}_{p}^{n}. \]
Así, $\mathbb{Q}^n_{p}$ con la distancia $d(x,y)=||x-y||_{p}$ es un espacio métrico completo. Se define \[ B^n_{r}(a)=\{x\in\mathbb{Q}_{p}:||x-a||_{p}\leq p^{r}\},\ r\in \mathbb{Z} \] como la bola $n$ dimensional de centro en $a\in \mathbb{Q}^n_{p} $ y radio $p^{r}$, y \[ S^n_{r}(a)=\{x\in\mathbb{Q}^n_{p}:||x-a||_{p}=p^{r}\},\ r\in \mathbb{Z} \] como la esfera $n$ dimensional de centro en $a\in \mathbb{Q}^n_{p}$ y radio $p^{r}$. Además \[ \mathbb{Q}^n_{p} \smallsetminus \lbrace 0 \rbrace =\cup_{r\in \mathbb{Z}}S^n_{r}(0). \]
La topología de $\mathbb{Q}_{p}$ tiene diferencias sorprendentes cuando se compara con la topología de $\mathbb{R}$; esto es consecuencia de la propiedad $3^{\prime}$. Nos permitimos mencionar algunas:
Una función complejo valuada $\varphi$ definida sobre $\mathbb{Q}^n_{p}$ es llamada localmente constante, si para cualquier $x\in\mathbb{Q}^n_{p}$ existe un entero $l(x)\in\mathbb{Z}$ tal que $\varphi\left( x+x^{\prime }\right) =\varphi\left( x\right) $, para $x^{\prime}\in B^n_{l(x)}(0)$. Una función $\varphi:\mathbb{Q}^n_{p}\rightarrow\mathbb{C}$ es llamada de Bruhat-Schwartz o función de prueba si es localmente constante y tiene soporte compacto. Estas funciones forman un $\mathbb{C}$-espacio vectorial denotado por $S(\mathbb{Q}^n_{p}):=S$. Toda función de Bruhat-Schwartz es una combinación lineal de funciones características de bolas. El espacio topológico dual $S'(\mathbb{Q}^n_{p})$ de $S(\mathbb{Q}^n_{p})$ está formado por las funcionales lineales continuas (también llamadas distribuciones). Por ejemplo, la distribución de Dirac $\delta$, definida como $\delta(\varphi)=\varphi(0)$, para $S(\mathbb{Q}^n_{p})$.
La función $\Psi(a x)=\exp\left( 2\pi i\left\{ ax\right\} _{p}\right) $ se denomina el carácter aditivo estándar de $\mathbb{Q}_{p}$, i.e. una aplicación continua $\mathbb{Q}_{p}$ al círculo unitario satisfaciendo $\Psi(y_0+y_1)=\Psi(y_0)\Psi(y_1)$, $y_0, y_1\in \mathbb{Q}_{p}$. Debido a que $(\mathbb{Q}^n_{p}, +)$ es un grupo topológico localmente compacto, éste tiene una única medida $d^nx$ (única hasta múltiplos positivos), llamada la medida de Haar de $\mathbb{Q}^n_{p}$. Esta medida es invariante bajo traslaciones (i.e., $d^nx=d^n\left( x+a\right) $) y se normaliza por medio de la condición $ {\textstyle\int\nolimits_{B^n_{0}(0)}} d^nx=1$.
Dados $\xi=(\xi_{1},\dots,\xi_{n})$ y $x=(x_{1},\dots,x_{n})\in\mathbb{Q}_{p}^{n}$, tomamos $\xi\cdot x:=\sum_{j=1}^{n}\xi_{j}x_{j}$. La transformada de Fourier de $\varphi\in S(\mathbb{Q}^n_{p})$ está definida como \[ (\mathcal{F}\varphi)(\xi)=\int_{\mathbb{Q}^n_{p}}\Psi(-\xi \cdot x)\varphi (\xi)\,d^nx\text{, } \, \, \, \xi\in\mathbb{Q}^n_{p}\text{.} \] La transformada de Fourier es un automorfismo de $S(\mathbb{Q}^n_{p})$ y satisface $\mathcal{F}(\mathcal{F}\varphi)(\xi)=\varphi(-x)$. Algunas veces usaremos la notación $\mathcal{F}_{\xi \to x}\varphi $ para la transformada de Fourier de una función de prueba. Para una discusión detallada de los fundamentos del análisis $p$-ádico, sugerimos al lector consultar [1]Albeverio S., Khrennikov A. Yu., Shelkovich V. M., Theory of p-adic distributions: linear and nonlinear models. Cambridge University Press, 2010., [9]Kochubei A.N., Pseudo-differential equations and stochastics over non-Archimedean fields. Marcel Dekker, Inc., New York, 2001., [17]Vladimirov V. S., Volovich I. V., Zelenov E. I., p-adic analysis and mathematical physics, World Scientific, 1994..
Las aplicaciones del análisis $p$-ádico a la física matemática están motivadas por dos ideas físicas. La primera es la conjetura en física de partículas que afirma que, a distancias en la escala de Planck, el espacio-tiempo tiene una estructura no arquimediana. La segunda idea viene de la física estadística, particularmente de los modelos que describen la relajación en vidrios, macro-moléculas y proteínas. Ha sido propuesto que la naturaleza no exponencial de tales “relajaciones” es una consecuencia de la estructura jerárquica del espacio de estados lo cual se puede interpretar en términos de estructuras $p$-ádicas; ver por ejemplo [13]Varadarajan, V. S., Reflections on quanta, symmetries, and supersymmetries, Springer, New York, 2011 x+236 pp. , [15]Dragovich B., Khrennikov A. Yu., Kozyrev S. V., Volovich, I. V., On p-adic mathematical physics, p-Adic Numbers Ultrametric Anal. Appl. 1 (2009), no. 1, 1-17..
B. Riemann descubrió que la geometría y la física están relacionadas a un nivel fundamental. En una famosa conferencia dada en 1854, la cual trato sobre de la determinación de la geometría del espacio físico, Riemman esboza su geometría riemanniana y propone que el espacio físico tiene una estructura de variedad riemanniana. Sin embargo, Riemann advirtió que su hipótesis no debe ser extrapolada a distancias muy pequeñas. A distancias muy pequeñas, el espacio-tiempo no es necesariamente una variedad en el sentido usual. Para una discusión a profundidad de estas ideas, recomendamos al lector [12]Varadarajan, V. S., Non-Archimedean models for space-time, Euroconference on Brance New World and Noncommutative Geometry (Torino, 2000) Modern Phys. Lett. A 16 (2001), no. 4-6, 387-395. , [13]Varadarajan, V. S., Reflections on quanta, symmetries, and supersymmetries, Springer, New York, 2011 x+236 pp. , [14]Varadarajan, V. S., Arithmetic quantum physics: why, what, and whither. Tr. Mat. Inst. Steklova 245 (2004), Izbr. Vopr. padich. Mat. Fiz. i Anal., 273--280; traducción en Proc. Steklov Inst. Math. 2004, no. 2(245) 258-265.. Esta idea permaneció oculta hasta la segunda mitad del siglo XX, cuando se comenzaron a construir modelos para explicar qué pasa a distancias muy pequeñas.
En la gravedad cuántica y la teoría de cuerdas “ha sido probado” lo siguiente: si $\Delta x$ es la incertidumbre en una medida de longitud, entonces, la desigualdad \[ \Delta x\geq\sqrt{\frac{hG}{c^{3}}}:=l_{P} \] se verifica. Aquí $h$ es la constante de Planck; $G$, la constante gravitacional, y $c$, la velocidad de la luz. Esta desigualdad es más fuerte que el principio de incertidumbre de Heinsenberg. La constante $l_{P} \cong10^{-33}cm$ es llamada la longitud de Planck. Entonces, la medida de distancias menores que la longitud de Planck es imposible. Este razonamiento implica que que no se pueden usar números reales en modelos que traten con la escala de Planck.
En los años ochenta, I. Volovich propuso utilizar números p-ádicos en lugar de números reales en los modelos físicos que tratan con situaciones a nivel de la escala de Planck; más exactamente, propuso que a distancias en la escala de Planck, el espacio-tiempo tiene una estructura no arquimediana; ver [18]Volovich I. V., p-adic String, Classical quantum gravity, 4 no. 4, L83-L87.. Este trabajo motivó a muchas personas a explorar varias formulaciones no arquimedianas de la teoría cuántica; ver, por ejemplo, [13, Capítulo 6]Varadarajan, V. S., Reflections on quanta, symmetries, and supersymmetries, Springer, New York, 2011 x+236 pp. , y las referencias allí mencionadas. Dado que no es posible fijar a priori un primo $p$, es necesario tratar todos los modelos $p$-ádicos al mismo tiempo. Esto lleva a una visión adélica del espacio-tiempo.
En física y bioquímica, un paisaje de energía es una aplicación de todas las posibles conformaciones de una entidad molecular, o las posiciones espaciales de moléculas que interactúan en un sistema y sus niveles de energía correspondientes. Matemáticamente, un paisaje de energía es una función continua $f:X\rightarrow\mathbb{R}$ que asocia a cada estado físico con una energía, donde $X$ es un dominio de $\mathbb{R}^{n}$. Las colinas y valles en el paisaje de energía corresponden a máximos y mínimos locales de $f$, respectivamente. Un sistema se denomina complejo cuando su paisaje de energía es complejo, esto es, tiene muchos mínimos locales, los cuales corresponden a estados metastables del sistema. Para analizar estos sistemas, los físicos han introducido varios principios a partir de los cuales es posible establecer modelos para el comportamiento de estos sistemas. Un primer paso consiste en agrupar estados: cuencas minimales corresponden a mínimos locales de energía, cuencas grandes (supercuencas) están constituidas por otras cuencas en una forma jerárquica. Después, se consideran transiciones entre cuencas; una transición requiere la superación de una barrera de energía. Este principio de modelación se denomina cinética entre cuencas (interbasin kinetics). El siguiente paso consiste en asociar, al paisaje de energía, un espacio ultramétrico (un árbol) que describe la organización jerárquica de las cuencas, y una función sobre este espacio ultramétrico que describe la distribución de las energías de activación entre cuencas. El espacio ultramétrico recibe el nombre de grafo de desconectividad (disconnectivity graph). Se ha propuesto que la dinámica de una clase grande de sistemas complejos, tales como vidrios, polímeros y proteínas, se puede describir como una caminata aleatoria sobre el árbol dirigido (el grafo de desconectividad) de cuencas asociado a un paisaje de energía complejo; ver figura 2.
El siguiente paso consiste en la construcción de un modelo de dinámica jerárquica basado en el árbol y la función de barreras de activación definida sobre él. En la construcción de tales modelos se usan los siguientes postulados: (i) el espacio de estados es partido en cuencas, y las cuencas están jerárquicamente partidas en subcuencas; así que forman un árbol dirigido de cuencas. (ii) La barrera de energía entre dos estados depende únicamente de las cuencas que contienen a los estados y no depende de la elección de los estados en las cuencas.
La dinámica está dada por \begin{equation} \frac{\partial f\left( i,t\right) }{\partial t}=\sum_{j}T\left( j\right) f\left( j,t\right) v(j)-\sum_{j\neq i}T\left( i,j\right) f\left( i,t\right) v\left( i\right), \label{Em} \end{equation} donde $f(i,t)$ es la población de partículas en el estado $i$ y en el tiempo $t$, los índices $i$,$j$ se usan para numerar los estados del sistema (los cuales corresponden a los mínimos locales de energía), $T\left( i,j\right) \geq0$ es la probabilidad por unidad de tiempo de transición de $i$ a $j$, y los $v(j)>0$ representan los volúmenes de las cuencas. La matriz $T\left( j,i\right) $ tiene una estructura de bloques especial. Físicamente, la ecuación anterior es una ecuación de difusión sobre un árbol.
Tomemos $v(j)=1$ y $T\left( i,j\right) =q\left( \left\vert i-j\right\vert _{p}\right) $, entonces la ecuación maestra (\ref{Em}) toma la forma \[ \frac{\partial f\left( i,t\right) }{\partial t}= {\displaystyle\int\limits_{p^{M}\mathbb{Z}_{p}/p^{N}\mathbb{Z}_{p}}} q\left( \left\vert i-j\right\vert _{p}\right) \left( f\left( i,t\right) -f\left( j,t\right) \right) d\mu\left( j\right) ,\text{ con }M< N, \] donde la integración (¡suma!) es con respecto a la medida del grupo discreto $p^{M}\mathbb{Z}_{p}/p^{N}\mathbb{Z}_{p}$. Formalmente, tomamos el límite $M\rightarrow-\infty$ y $N\rightarrow+\infty$ para obtener la siguiente ecuación de difusión continua $p$-ádica (ecuación parabólica $p$-ádica): \begin{equation} \frac{\partial f(x,t)}{\partial t}=\int_{\mathbb{Q}_{p}}q(|x-y|_p)(f(x,t)-f(y,t))dy.\label{Em2} \end{equation} Ahora, si tomamos $q(|x|_p)=\frac{1-p^{\alpha}}{1-p^{-\alpha-1}}|x|^{-1-\alpha}_p$, $\alpha>0$, (\ref{Em2}) se convierte en la ecuación $p$-ádica del calor: \begin{equation} \frac{\partial f(x,t)}{\partial t}+D_x^{\alpha}f(x,t))=0, x\in \mathbb{Q}_p, t\geq 0,\label{Em3} \end{equation} donde \[ (D_x^{\alpha}\varphi )(x)= \mathcal{F}_{x\to \xi}^{-1}(|\xi|^{\alpha}_p(\mathcal{F}_{\xi \to x}\varphi)),\] es el operador de Vladimirov. La figura 3 muestra una comparación numérica entre las ecuaciones del calor $p$-ádicas y arquimedianas.
El problema de Cauchy para (\ref{Em3}) con condición inicial $f(x,0)$ igual a la función característica de la bola unitaria tiene una interpretación física relevante: se puede verificar que $\int_{\mathbb{Z}_{p}}f\left( x,t\right) dx\sim t^{-\frac{1} {\alpha}}$, donde la integral representa la probabilidad de permanecer en la bola unitaria dado que, inicialmente, el sistema estaba en la bola unitaria. Este tipo de comportamiento aparece experimentalmente en la unión del CO mioglobina. Para una discusión a profundidad, le sugerimos al lector el libro [2]Frauenfelder H., Chan S.S., Chan W.S. (editor), Austin R. H., Schulz C. E., Nienhaus G. U., Young R. D., The Physics of Proteins: An Introduction to Biological Physics and Molecular Biophysics, Springer, 2010., así como las referencias, [3]Avetisov V. A., Introduction to Non-Archimedean Physics of Proteins. Minicourse in First International Conference on Modeles of complex heierarchic systems and non-Archimedean Analysis, disponible en http://www.math.cinvestav.mx/ICMCHS2013/minicourse., [4]Avetisov V. A., Bikulov A. H., Kozyrev S. V., Application of p-adic analysis to models of breaking of replica symmetry, J. Phys. A 32 (1999), no. 50, 8785-8791., [5]Avetisov V. A., Bikulov A. H., Kozyrev S. V., Osipov V. A., p-adic models of ultrametric diffusion constrained by hierarchical energy landscapes, J. Phys. A 35 (2002), no. 2, 177-189., [10]Kozyrev S. V., Methods and Applications of Ultrametric and p-Adic Analysis: From Wavelet Theory to Biophysics, Proc. Steklov Inst. Math. 274 (2011), S1-S84..
En primer lugar, debemos mencionar que hay dos tipos completamente diferentes de análisis $p$-ádico, un primer tipo considera funciones de $\mathbb{Q}^n_{p}$ en $\mathbb{C}$, y un segundo tipo de $\mathbb{Q}^n_{p}$ en $\mathbb{Q}_{p}$. En el primer caso, no es posible usar la noción de derivada como cociente de incrementos. En lugar se usa el concepto de derivada fraccionaria.
Sea $\alpha>0$, definimos \[ (D^{\alpha}\varphi)(x)=\mathcal{F}_{\xi \to x}^{-1}(||\xi||_p^{\alpha}(\mathcal{F}_{ x \to \xi}\varphi))\] para $\varphi \in S(\mathbb{Q}_p^{n})$. Este operador admite la extensión: \[ \left( D^{\alpha}\varphi\right) \left( x\right) =\frac{1-p^{\alpha} }{1-p^{-\alpha-n}} {\displaystyle\int\limits_{\mathbb{Q}^n_{p}}} || y||_{p}^{-\alpha-n}\left[ \varphi\left( x-y\right) -\varphi\left( x\right) \right] d^ny \] a funciones localmente constantes que satisfacen \[ {\displaystyle\int\limits_{|| x ||_{p}>1}} ||x||_{p}^{-\alpha-1}\left\vert \varphi\left( x\right) \right\vert d^nx<\infty. \] El operador pseudodiferencial $D^{\alpha}$ es el análogo $p$-ádico de la derivada. Cuando $n=1$ este operador se llama operador de Vladimirov y cuando $n>1$ se llama operador de Taibleson. El lector interesado puede consultar [1]Albeverio S., Khrennikov A. Yu., Shelkovich V. M., Theory of p-adic distributions: linear and nonlinear models. Cambridge University Press, 2010., [9]Kochubei A.N., Pseudo-differential equations and stochastics over non-Archimedean fields. Marcel Dekker, Inc., New York, 2001., [11]Rodríguez-Vega J. J., Zúñiga-Galindo W. A., Taibleson operators, p-adic parabolic equations and ultrametric diffusion, Pacific J. Math. 237 (2008), no. 2, 327-347..
Tomemos $\mathbb{R}_{+}:=\left\{ x\in\mathbb{R};x\geq0\right\}. $ En [7]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503. se introdujo una familia grande de operadores pseudodiferenciales que generalizan los operadores $D^{\alpha}.$
Fijemos una función \[ w:\mathbb{Q}_{p}^{n}\rightarrow\mathbb{R}_{+} \] que satisface las siguientes propiedades:
La condición (iii) implica que \[ {\int\limits_{\left\Vert y\right\Vert _{p}\geq p^{M}}}\frac{d^{n}y}{w\left( \left\Vert y\right\Vert _{p}\right) }<\infty. \]
Se define el operador \begin{equation} (\boldsymbol{W}\varphi)(x)=\kappa{\int\limits_{\mathbb{Q}_{p}^{n}}} \frac{\varphi\left( x-y\right) -\varphi\left( x\right) }{w\left( ||y||_p \right) }d^{n}y \text{,} \, \, \text{para }\varphi\in S\text{,} \label{1W} \end{equation} done $\kappa$ es una constante positiva.
El operador (\ref{1W}) resulta ser un operador pseudodiferencial con símbolo dado por \[ A_{w}\left( \xi\right) :={\int\limits_{\mathbb{Q}_{p}^{n}}}\frac {1-\Psi\left( -y\cdot\xi\right) }{w\left( || y||_p \right) }d^{n}y, \] éste es una función radial y continua, ver [7, Lema 3.2]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503.; además, para $A_{w}$, se conoce el comportamiento asintótico para $\xi \to 0$ y $\xi \to +\infty$; ver [7, Lema 3.4]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503..
El núcleo de calor $p$-ádico se define como: \[ Z\left( x,t\right) =\mathcal{F}_{\xi\rightarrow x}^{-1}\left( e^{-\kappa tA_{w}(|| \xi|| _{p})}\right) = {\textstyle\int\limits_{\mathbb{Q}^n_{p}}} \Psi\left( x \cdot \xi\right) e^{-\kappa tA_{w}(|| \xi|| _{p})}d^n\xi. \] A partir del [7, Lema 3.4]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503. se prueba que $Z\left( x,t\right)\in L^1(\mathbb{Q}_p^n)\cap L^2(\mathbb{Q}_p^n)$, para $t>0$, cuando se considera a $Z\left( x,t\right)$ como función de $x$ para un $t$ fijo se denota por $Z_t\left(x\right)$.
El siguiente resultado resume las principales propiedades del núcleo del calor.
Recientemente en [7]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503., los autores estudiaron el siguiente problema de Cauchy: \begin{equation} \left\{ \begin{array} [c]{ll} \frac{\partial u}{\partial t}(x,t)-(\boldsymbol{W}u)(x,t)=g(x,t), & x\in\mathbb{Q}_{p}^{n},\, \,t\geq0\\ & \\ u\left( x,0\right) =\varphi(x). \end{array} \right. \label{Cauchy} \end{equation} El cual tiene como solución \[ u\left( x,t\right) = {\displaystyle\int\limits_{\mathbb{Q}_{p}^n}} Z\left( x-\xi,t\right) \varphi\left( \xi\right) d^n\xi+ {\displaystyle\int\limits_{0}^{t}} {\displaystyle\int\limits_{\mathbb{Q}^n_{p}}} Z\left( x-\xi,t-\tau\right) g\left( \xi,\tau\right) d^n\xi d\tau;\] ver [7, Teorema 6.5]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503..
La ecuación clásica del calor está asociada al movimiento browniano. Se trata de un movimiento aleatorio sobre $\mathbb{R}$, en el cual, la partícula se mueve aleatoriamente a través de trayectorias continuas pero no diferenciables. Nuestro siguiente objetivo es explicar que existe una interpretación probabilística análoga para la solución fundamental de (\ref{Cauchy}).
La construcción de un modelo de movimiento aleatorio sobre $\mathbb{Q}^n_p$ análogo al movimiento browniano hace uso de la maquinaria clásica de procesos de Markov sobre espacios métricos; ver, por ejemplo, [6]Dynkin E. B., Markov processes. Vol. I. Springer-Verlag, 1965..
Definamos \[ p\left( t,x,y\right) =Z\left( x-y,t\right),\, \, t>0, \] y \[ P(t,x,B)= \begin{cases} \int_{B}p(t,y,x)d^{n}y & t>0,\quad x\in\mathbb{Q}_{p}^{n}\\ \boldsymbol{1}_{B}(x) & t=0, \end{cases} \] donde $B$ es un subconjunto de Borel de $\mathbb{Q}_{p}^{n}$. $P(t,x,B)$ representa la probabilidad de que una partícula salte al conjunto $B$, después de $t$ segundos, siendo que estaba en la posición $x$. De manera más técnica, podemos decir que $Z\left( x,t\right) $ es la función de densidad de transición de un proceso estocástico de Markov $X(t,\omega)$, el cual es homogéneo en el espacio y en el tiempo, y cuyas trayectorias $X_{\omega}(t)$, curvas en $\mathbb{Q}_{p}^{n}$, son continuas por la derecha con discontinuidades solamente de salto; ver [7, Teorema 5.3]Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503..
Considere el siguiente problema de Cauchy \[ \left\{ \begin{array} [c]{ll} \frac{\partial u\left( x,t\right) }{\partial t}=-\left( \boldsymbol{W}u\right) \left( x,t\right) \text{,} & x\in \mathbb{Q}^n_{p}\text{, }t>0\\ & \\ u\left( x,0\right) =1_{\mathbb{Z}^n_{p}}(x). & \end{array} \right. \] Cuya solución está dada por \[ u(x,t)=\int_{\mathbb{Q}_p^n}Z(x-\xi,t)1_{\mathbb{Z}_p^n}(\xi)d^n\xi,\] donde $Z(x,t)$ es la densidad de transición de $X(t,\omega)$. Desde un punto de vista físico, a $u(x,t)$ le podemos asociar un movimiento aleatorio en $\mathbb{Q}_{p}^{n}$ cuyas trayectorias comienzan en la bola unitaria y son curvas que tienen únicamente discontinuidades de salto; ver figura 4. El espacio de todas las posibles trayectorias se denota como $\Upsilon$.
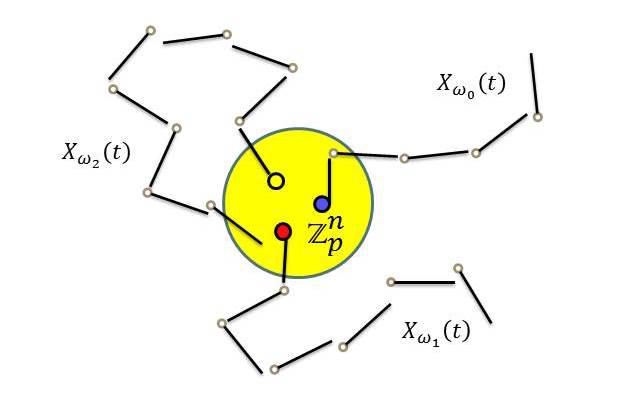
Figura 4.
Un problema importante consiste en estimar el tiempo en que una trayectoria regresa a la bola unitaria. De manera precisa tenemos
[1] Albeverio S., Khrennikov A. Yu., Shelkovich V. M., Theory of $p$-adic distributions: linear and nonlinear models. Cambridge University Press, 2010.
[2] Frauenfelder H. (autor), Chan S.S. (editor), Chan W.S. (editor), Austin R. H.(contribuidor), Schulz C. E. (contribuidor), Nienhaus G. U. (contribuidor), Young R. D. (contribuidor), The Physics of Proteins: An Introduction to Biological Physics and Molecular Biophysics, Springer, 2010.
[3] Avetisov V. A., Introduction to Non-Archimedean Physics of Proteins. Minicourse in First International Conference on Modeles of complex heierarchic systems and non-Archimedean Analysis, disponible aquí.
[4] Avetisov V. A., Bikulov A. H., Kozyrev S. V., Application of p-adic analysis to models of breaking of replica symmetry, J. Phys. A 32 (1999), no. 50, 8785-8791.
[5] Avetisov V. A., Bikulov A. H., Kozyrev S. V., Osipov V. A., $p$-adic models of ultrametric diffusion constrained by hierarchical energy landscapes, J. Phys. A 35 (2002), no. 2, 177-189.
[6] Dynkin E. B., Markov processes. Vol. I. Springer-Verlag, 1965.
[7] Chacón-Cortes L.F., Zúñiga-Galindo W. A., Nonlocal Operators, Parabolic-Type Equations, and Ultrametric Random Walks, J. Math. Phys. 54 (2013), 113503.
[8] Taibleson M. H., Fourier analysis on local fields, Princeton University Press, 1975.
[9] Kochubei A.N., Pseudo-differential equations and stochastics over non-Archimedean fields. Marcel Dekker, Inc., New York, 2001.
[10] Kozyrev S. V., Methods and Applications of Ultrametric and $p$-Adic Analysis: From Wavelet Theory to Biophysics, Proc. Steklov Inst. Math. 274 (2011), S1-S84.
[11] Rodríguez-Vega J. J., Zúñiga-Galindo W. A., Taibleson operators, $p$-adic parabolic equations and ultrametric diffusion, Pacific J. Math. 237 (2008), no. 2, 327-347.
[12] Varadarajan, V. S., Non-Archimedean models for space-time, Euroconference on Brance New World and Noncommutative Geometry (Torino, 2000) Modern Phys. Lett. A 16 (2001), no. 4-6, 387-395.
[13] Varadarajan, V. S., Reflections on quanta, symmetries, and supersymmetries, Springer, New York, 2011 x+236 pp.
[14] Varadarajan, V. S., Arithmetic quantum physics: why, what, and whither. Tr. Mat. Inst. Steklova 245 (2004), Izbr. Vopr. $p$adich. Mat. Fiz. i Anal., 273--280; traducción en Proc. Steklov Inst. Math. 2004, no. 2(245) 258-265.
[15] Dragovich B., Khrennikov A. Yu., Kozyrev S. V., Volovich, I. V., On $p$-adic mathematical physics, p-Adic Numbers Ultrametric Anal. Appl. 1 (2009), no. 1, 1-17.
[16] Rammal R., Toulouse G., Virasoro M. A., Ultrametricity for physicists, Rev. Modern Phys. 58 (1986), no. 3, 765-788.
[17] Vladimirov V. S., Volovich I. V., Zelenov E. I., $p$-adic analysis and mathematical physics, World Scientific, 1994.
[18] Volovich I. V., $p$-adic String, Classical quantum gravity, 4 no. 4, L83-L87.
[19] Zúñiga-Galindo W. A., Parabolic equations and Markov processes over p-adic fields, Potential Anal. 28 (2008), no. 2, 185--200.

