

En esta serie de tres artículos, damos una exposición de varios resultados y problemas abiertos en tres áreas de la combinatoria algebraica y geométrica: las matrices totalmente no negativas, las representaciones de $S_n$, y los arreglos de hiperplanos. Esta tercera parte presenta una introducción a los arreglos de hiperplanos desde un punto de vista combinatorio.
En marzo de 2003, se llevó a cabo el Primer Encuentro Colombiano de Combinatoria en Bogotá, Colombia. Como parte del encuentro, se organizaron tres minicursos, dictados por Federico Ardila, Mercedes Rosas, y Mark Skandera. Esta serie resume el material presentado en estos cursos en tres artículos: I. Matrices totalmente no negativas y funciones simétricas [1]F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. I. Matrices totalmente no negativas y funciones simétricas. universo.math, 1 no.1 (2014) artículo 5., II. Las funciones simétricas y la teoria de las representaciones [2]F. Ardila, E. León, M. Rosas, and M. Skandera, Tres lecciones en combinatoria algebraica. II. Representaciones del grupo simétrico, universo.math, 1 no.2 (2014) artículo 5., y III. Arreglos de hiperplanos [3]lo estás leyendo.
En esta tercera parte se presenta una introducción a los arreglos de hiperplanos desde un punto de vista combinatorio. Estudiaremos las regiones, el polinomio característico, y el poset de intersecciones de un arreglo. También estudiaremos algunos arreglos especiales que están relacionados con objetos combinatorios clásicos.
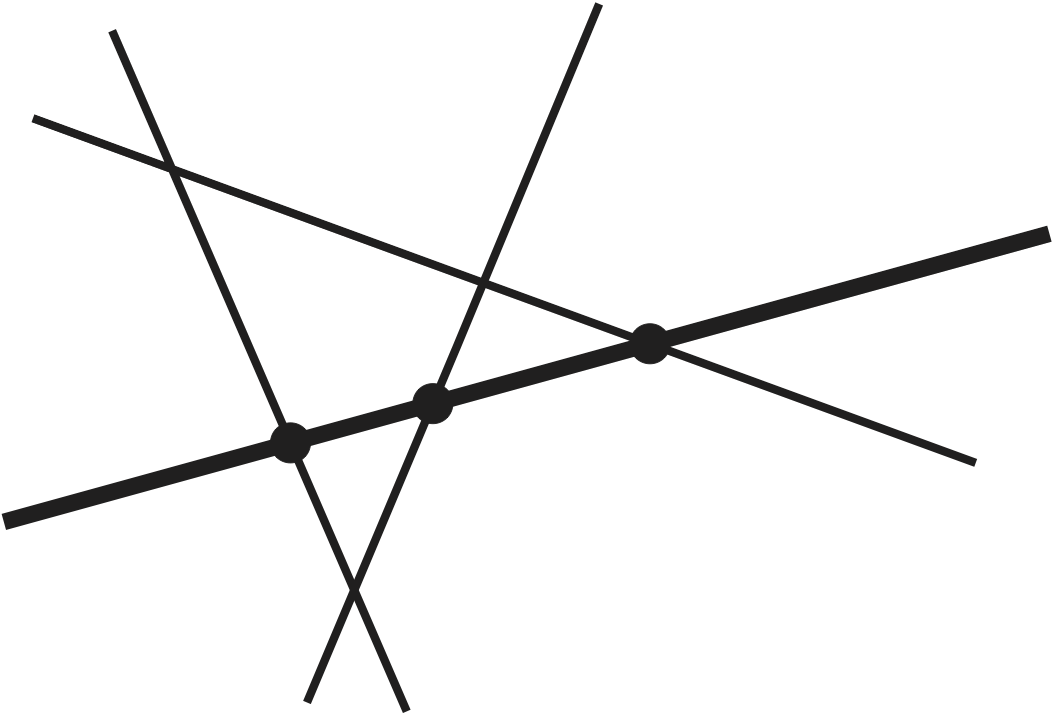
La siguiente pregunta servirá como motivación: si trazamos $n$ líneas rectas en el plano $\mathbb{R}^2$, ¿cuál es el mayor número de regiones que podemos formar?
Es fácil ver que, para lograr que el número de regiones sea máximo, las rectas deben estar en posición general, es decir:
En efecto, si algunas rectas del arreglo no cumplen estas propiedades, podemos moverlas un poco de manera que el número de regiones aumente. Lo sorprendente es que las dos condiciones anteriores son suficientes y determinan de manera única el número de regiones que se forman.
Demostración. Demostremos por inducción que los números $\mathrm{r}(n)$ y $\mathrm{b}(n)$ de regiones y de regiones acotadas determinadas por $n$ rectas genéricas dependen sólo de $n$, y satisfacen las recurrencias $$\mathrm{r}(n)=\mathrm{r}(n-1)+n, \qquad \qquad \mathrm{b}(n)=\mathrm{b}(n-1)+(n-2),$$ El caso $n=0$ es claro. Consideremos $n$ rectas en posición general. Si borramos una de ellas, las otras $n-1$ dividen al plano en $\mathrm{r}(n-1)$ regiones, $\mathrm{b}(n-1)$ de las cuales son acotadas. Al volver a introducir la recta borrada, ésta dividirá algunas de estas regiones en dos. Las $n-1$ rectas dividen la nueva recta en $n$ sectores, de las cuales $n-2$ son acotadas. Por lo tanto, la nueva recta divide $n$ de las $\mathrm{r}(n-1)$ regiones, y exactamente $n-2$ de éstas introducen una nueva región acotada. Las fórmulas explícitas para $\mathrm{r}(n)$ y $\mathrm{b}(n)$ se siguen. ▢
Ahora generalizaremos el resultado anterior a tres dimensiones:
Si trazamos $n$ planos en $\mathbb{R}^3$, ¿cuál es el mayor número de regiones que podemos formar?
Igual que en el caso anterior, es claro que, para obtener el máximo número de regiones, es necesario que los planos estén en posición general en el siguiente sentido:
Nuevamente, las tres condiciones anteriores determinan de manera única el número de regiones en las que se divide el espacio, y también el número de regiones acotadas, para cada valor de $n$. En este caso, llamaremos $\mathrm{r}_3(n)$ al número de regiones que son determinadas por $n$ planos en posición general, y $\mathrm{b}_3(n)$ al número de regiones acotadas.
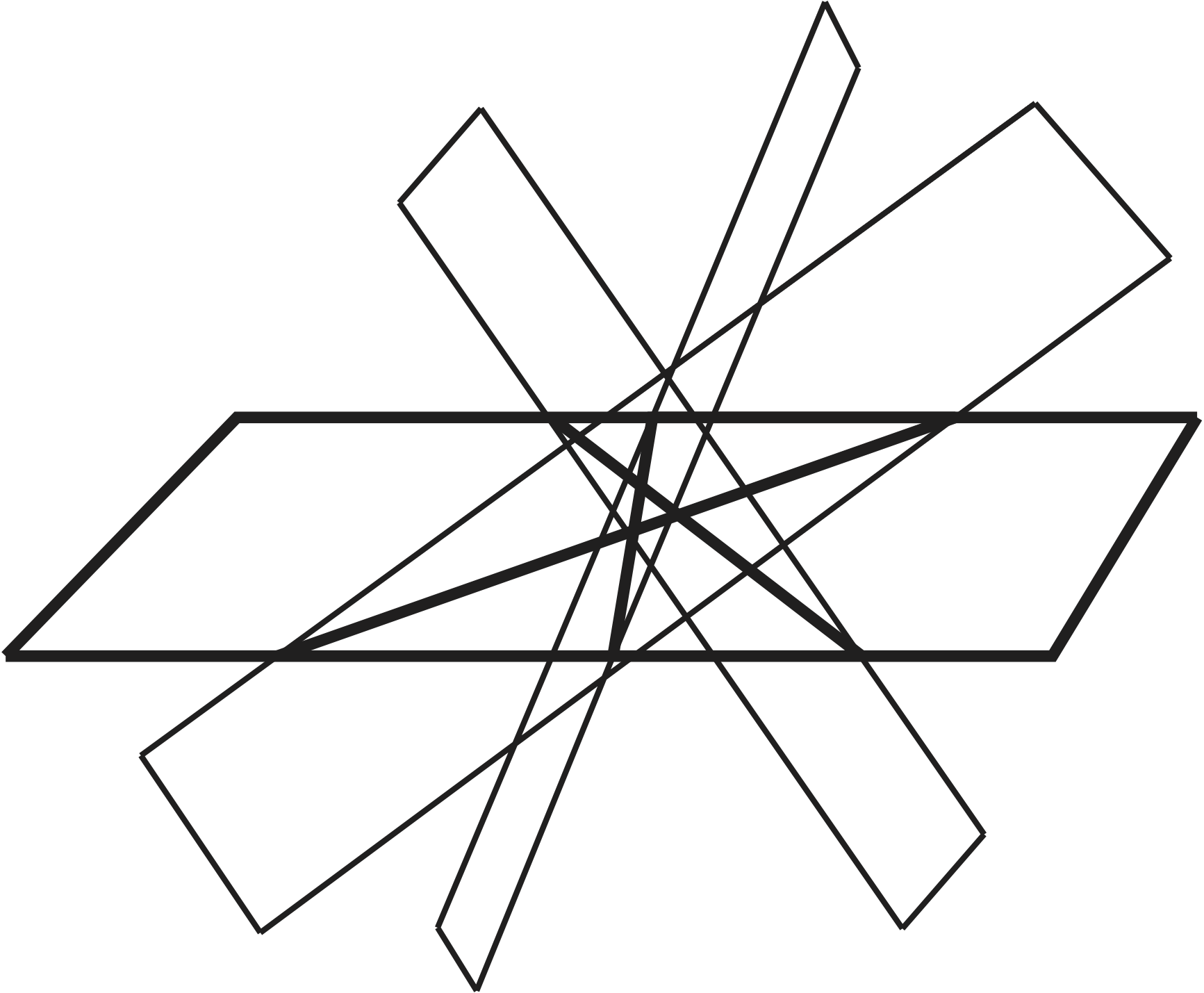
Demostración. Nuevamente, consideramos un plano especial $P$ de un arreglo genérico de $n$ planos para obtener relaciones recursivas para $\mathrm{r}_3(n)$ y $\mathrm{b}_3(n)$. Quitando este plano del arreglo, obtenemos un arreglo con $n-1$ planos en posición general que genera $\mathrm{r}_3(n-1)$ regiones, entre las cuales hay $\mathrm{b}_3(n-1)$ regiones acotadas.
Los otros $n-1$ planos determinan $n-1$ rectas en $P$. Si los planos están en posición general, las rectas en $P$ se encuentran en posición general. Por lo tanto, ellas forman ${n\choose 2}+{n\choose 1}+{n\choose 0}$ regiones, de las cuales ${n\choose 2}-{n\choose 1}+{n\choose 0}$ son acotadas. Al volver a colocar el plano $P$, el número de estas regiones que son divididas en dos es igual al número de regiones que se forman en $P$; es decir, $r_2(n-1):= r(n-1) = {n-1 \choose 2}+{n-1 \choose 1}+{n-1 \choose 0}$. Cada región acotada en $P$ genera una nueva región acotada. Así obtenemos que \begin{equation*} \begin{split}\mathrm{r}_3(n)&=\mathrm{r}_3(n-1)+\mathrm{r}_2(n-1)=\mathrm{r}_3(n-1)+{n-1\choose 2}+{n-1\choose 1}+{n-1\choose 0},\\ \mathrm{b}_3(n)&=\mathrm{b}_3(n-1)+\mathrm{b}_2(n-1)=\mathrm{b}_3(n-1)+{n-1\choose 2}-{n-1\choose 1}+{n-1\choose 0}. \end{split} \end{equation*} De las recurrencias anteriores, se obtienen las fórmulas deseadas. ▢
Estos dos ejemplos sugieren una generalización natural en cualquier dimensión. Es natural conjeturar que cualquier arreglo de $n$ hiperplanos genéricos en $\mathbb{R}^d$ tiene un cierto número de regiones $\mathrm{r}_d(n)$ y regiones acotadas $\mathrm{b}_d(n)$, y es fácil adivinar cuáles son esos números. Esta generalización es correcta, y la demostraremos en el Teorema 3.11. Pero antes de hacerlo, debemos precisar el significado de los diferentes conceptos involucrados. Debemos saber qué son los hiperplanos, las regiones, y qué significa estar en posición general en el caso de dimensión $d$. En la siguiente sección introducimos estas definiciones.
Si $v=(v_1,\ldots,\,v_d)$ y $x=(x_1,\ldots,x_n)$ son vectores en $\mathbb{R}^d$, denotamos el producto punto de $v$ y $x$ por $v\cdot x=v_1x_1+v_2x_2+\cdots +v_dx_d$.
Si $S$ es un subespacio afín y $x\in S$, entonces la translación $S-x$ es un subespacio vectorial de $\mathbb{R}^d$. Esto nos permite definir la dimensión de $S$ como la dimensión de $S-x$ como espacio vectorial. Se encuentra, por ejemplo, que la dimensión de un hiperplano $H$ es $d-1$ (pues su translación resulta ser el espacio ortogonal al vector $v$, tomando a $H$ como en la Definición 2.1). Toda intersección de hiperplanos forma un subespacio afín, y todo subespacio afín de dimensión $k$ se puede expresar como la intersección de $d-k$ hiperplanos en $\mathbb{R}^d$.
Cada hiperplano $H=\{x\in \mathbb{R}^d:v\cdot x=a\}$ divide a $\mathbb{R}^d$ en dos regiones, donde $v\cdot x < a$ y $v\cdot x > a$ respectivamente.
Dado un arreglo de hiperplanos $\mathcal{A}$, éste divide al espacio en varias componentes conexas, llamadas regiones. Si $\mathcal{A}$ está formado por $n$ hiperplanos \[ H_i=\{x \in \mathbb{R}^d:v_i\cdot x=a_i\}, \] donde $v_i\in \mathbb{R}^d$ para $1 \leq i \leq n$, cada región de $\mathcal{A}$ puede ser descrita con un sistema de desigualdades que tiene solución en $\mathbb{R}^d$, donde se selecciona una desigualdad de la forma \[ v_i\cdot x< a_i\qquad\textrm{o}\qquad v_i\cdot x> a_i \] para cada $1 \leq i \leq n$.
Las condiciones anteriores pueden resumirse diciendo que, para todo subconjunto de $r$ hiperplanos del arreglo, con $0\leq r\leq d$, la intersección es un subespacio afín de dimensión $d-r$; y que, para más de $d$ hiperplanos, la intersección siempre es vacía. Podemos ver la intersección de un conjunto de $r$ hiperplanos como el conjunto solución de un sistema de $r$ ecuaciones con $d$ incógnitas. Un arreglo es genérico cuando cualesquiera $r$ ecuaciones son linealmente independientes.
Luego de precisar estos conceptos, es posible demostrar la generalización natural de los Teoremas 1.1 y 1.2 en cualquier dimensión. Sin embargo, procederemos de manera diferente; vamos a desarrollar herramientas generales que nos permitan entender esta situación más conceptualmente.
Recordemos que un conjunto parcialmente ordenado o posetdel inglés "partially ordered set" $P$ es un conjunto $P$ junto con una relación binaria $\leq$ de "orden parcial" tal que:
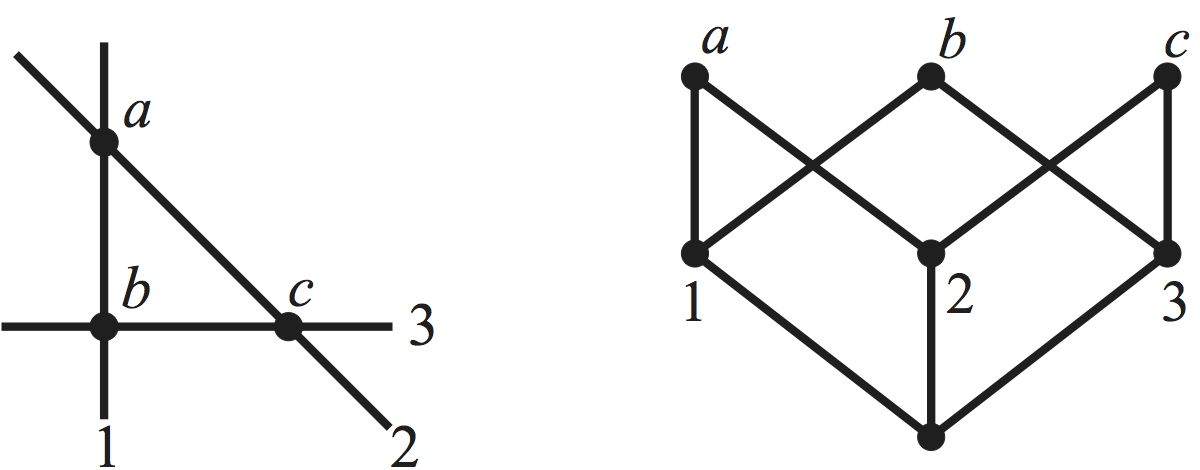
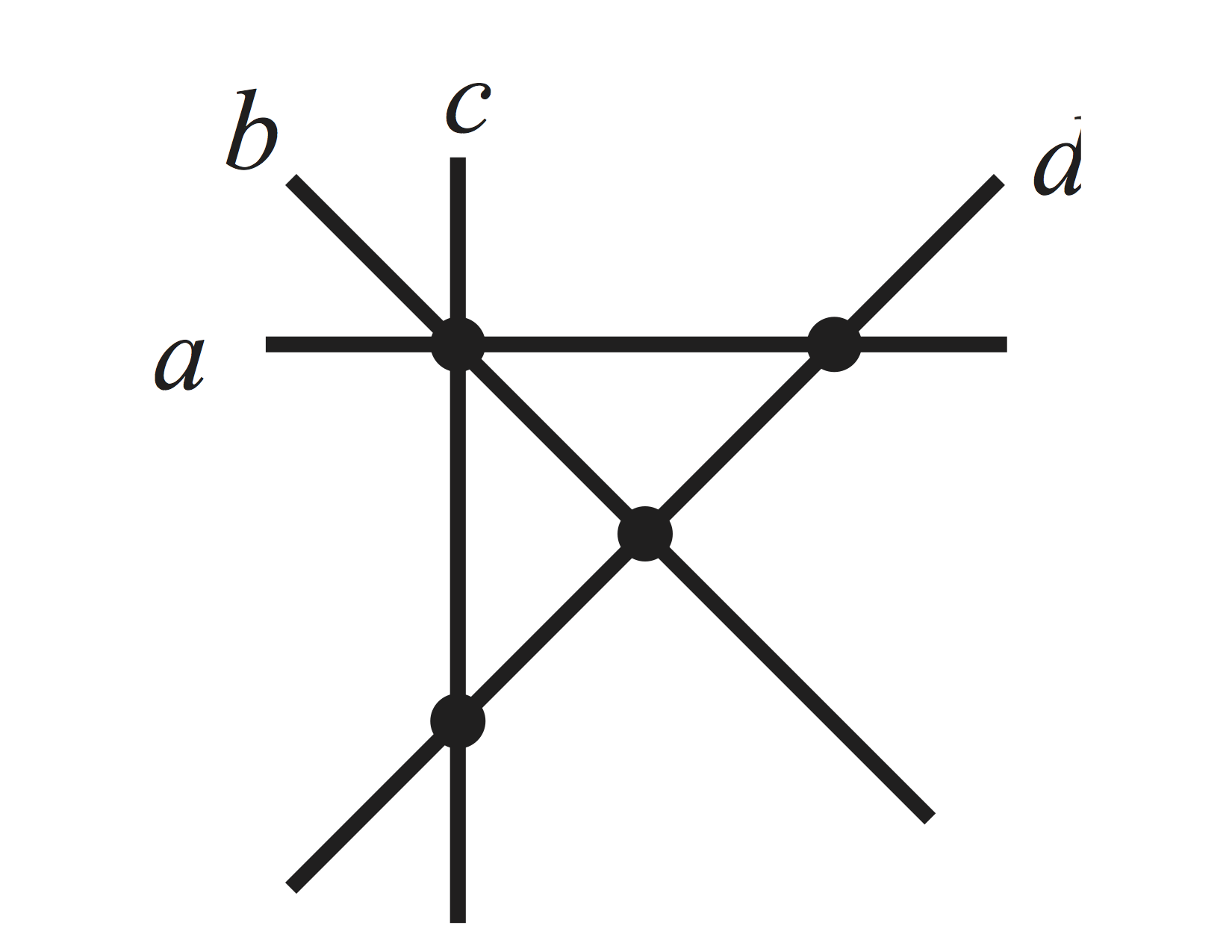
La Figura 3 muestra un arreglo en $\mathbb{R}^2$ y su poset de intersección.
Gian-Carlo Rota [13]G. C. Rota. On the Foundations of Combinatorial Theory I: Theory of Möbius Functions. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, 2 (1964) 340-368. fue el precursor del estudio de la función de Möbius de un poset, una teoría muy elegante que conecta resultados en la teoría de los números (la función de Möbius clásica) con la combinatoria enumerativa (la fórmula de inclusión-exclusión), y la topología (la característica de Euler), entre otras. Nosotros aplicaremos esta teoría a los arreglos de hiperplanos.
Vale la pena tener en cuenta que la función de Möbius y el polinomio característico de un arreglo $\mathcal{A}$ dependen únicamente del poset $L(\mathcal{A})$ y la dimensión del espacio.
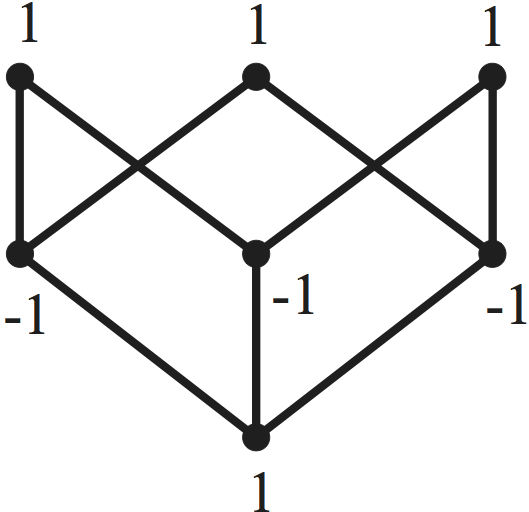
La Figura 4 muestra los valores de la función $\mu$ en el poset $L(\mathcal{A})$ del ejemplo 3.2. El polinomio característico de $\mathcal{A}$ es $\chi_{\mathcal{A}}(t)=t^2-3t+3.$
Demostración. En este caso, los elementos de $L(\mathcal{A})$ de dimensión $d-k$ son todas las posibles intersecciones de $k$ hiperplanos, que son todas distintas; hay ${n\choose k}$ de ellas. Además, dado un elemento $X$ de $L(\mathcal{A})$ de dimensión $d-k$ que es la intersección de $\mathcal{B} \subseteq \mathcal{A}$ con $|\mathcal{B}|=k$, los elementos $Y$ tales que $Y \leq X$ son las intersecciones de los subconjuntos de $\mathcal{B}$. Por lo tanto hay ${k\choose l}$ elementos de $L(\mathcal{A})$ de dimensión $d-l$ menores que $X$. Usando esto, demostraremos inductivamente que $\mu(X)=(-1)^k$.
Para ver esto, primero observamos que $\mu(\mathbb{R}^d)=(-1)^0=1$. Para otro elemento $X\in L(\mathcal{A})$ de dimensión $d-k$, se encuentra que $$\mu(X)=-\sum_{Y< X} \mu(Y)= -\left(1-{k\choose 1}+{k\choose 2}-\cdots+(-1)^{k-1}{k\choose k-1}\right)=(-1)^k,$$ ya que la suma contiene $k \choose l$ elementos de dimensión $d-l$, cuya función de Möbius es $(-1)^l$ por inducción. El resultado se sigue. ▢
Existe una clara relación entre el polinomio característico de un arreglo genérico (Teorema 3.6) y los números de regiones y de regiones acotadas de tal arreglo para $d=2,3$ (Teoremas 1.1 y 1.2). Nuestro siguiente objetivo es aclarar esta relación en el Teorema 3.9.
Si un arreglo $\mathcal{A}$ no es esencial, la intersección de los hiperplanos de $\mathcal{A}$ es un espacio afín $L$. Podemos esencializar el arreglo, considerando el arreglo $\mathcal{A}^{es} = \{H\cap L^{\perp} \, : \, H \in \mathcal{A}\}$ de hiperplanos en el espacio $L^{\perp}$ ortogonal a $L$. Es claro que $\mathcal{A}$ y $\mathcal{A}^{es}$ tienen el mismo poset de intersección, y también que las regiones de estos dos arreglos están en biyección.
La definición anterior es necesaria ya que un arreglo no esencial no tiene regiones acotadas. Para simplificar, de ahora en adelante, cuando hablemos de regiones acotadas estaremos refiriéndonos a las regiones relativamente acotadas. Denotaremos entonces por $\mathrm{b}(\mathcal{A})$ al número de regiones acotadas de un arreglo. El siguiente teorema relaciona el número de regiones y de regiones acotadas de un arreglo con su polinomio característico.
Este teorema se demostrará usando una idea que ya hemos expuesto en los ejemplos iniciales, que se conoce como el método de eliminación/contracción. Ésta es una de las técnicas más útiles para llevar a cabo argumentos inductivos en arreglos de hiperplanos. Consiste en expresar cierta información de un arreglo en términos de los siguientes dos arreglos más peque\~nos:
Demostración del Teorema 3.9. Usando el mismo argumento de los Teoremas 1.1 y 1.2, obtenemos las fórmulas recursivas $$ \mathrm{r}(\mathcal{A})= \mathrm{r}(\mathcal{A}-H)+\mathrm{r}(\mathcal{A}/H), \qquad \qquad \mathrm{b}(\mathcal{A})=\mathrm{b}(\mathcal{A}-H)+\mathrm{b}(\mathcal{A}/H). $$ Basta ver que cada región de $\mathcal{A}/H$ está partiendo una región de $\mathcal{A}-H$ en dos, dando como resultado todas las regiones de $\mathcal{A}$. Algo similar sucede con las regiones acotadas.
Por otro lado, vamos a demostrar la siguiente fórmula recursiva para el polinomio característico de un arreglo $$ \chi_{\mathcal{A}}(q)=\chi_{\mathcal{A}-H}(q)-\chi_{\mathcal{A}/H}(q). $$
Para hacerlo, vamos a demostrar que $$ \mu_{\mathcal{A}}(X)=\mu_{\mathcal{A}-H}(X)-\mu_{\mathcal{A}/H}(X), $$ para todo $X\in L(\mathcal{A})$, donde el subíndice indica el arreglo en el cual se calcula la función. Si $X \notin L(\mathcal{A}')$ definimos $\mu_{\mathcal{A}'}(X)=0$.
Esto lo podemos ver por inducción en $d-l$ donde $l$ es la dimensión de $X$. Es decir, por inducción, comenzando por los menores elementos de $L(\mathcal{A})$. Para $X=\mathbb{R}^d$, se cumple que $X\notin \mathcal{A}/H$, por lo que $\mu_{\mathcal{A}}(\mathbb{R}^d)=\mu_{\mathcal{A}-H}(\mathbb{R}^d)-\mu_{\mathcal{A}/H}(\mathbb{R}^d)=1$. Para los hiperplanos del arreglo también se verifica la identidad anterior, notando que si $X\neq H$, entonces $\mu_{\mathcal{A}/H}(X)=0$, mientras que si $X=H$, entonces $\mu_{\mathcal{A}-H}(X)=0$ y $\mu_{\mathcal{A}/H}(H)=1$. Para los demás elementos $X\in L(\mathcal{A}),$ se tiene por hipótesis de inducción que \begin{eqnarray*} \mu_{\mathcal{A}}(X)&=&-\sum_{Y<_\mathcal{A} X}\mu_{\mathcal{A}}(Y)=-\sum_{Y<_\mathcal{A} X}\mu_{\mathcal{A}-H}(Y)+\sum_{Y<_\mathcal{A} X}\mu_{\mathcal{A}/H}(Y)\\ &=&-\sum_{Y<_{\mathcal{A}-H} X}\mu_{\mathcal{A}-H}(Y)+\sum_{Y< _{\mathcal{A}/H} X}\mu_{\mathcal{A}/H}(Y) =\mu_{\mathcal{A}-H}(X)-\mu_{\mathcal{A}/H}(X) \end{eqnarray*} donde $Y <_\mathcal{B} X$ denota que $Y< X$ en el poset de intersección del arreglo $\mathcal{B}$. El resultado se sigue. ▢
Como corolario del teorema anterior, se encuentra que el número de regiones y el número de regiones acotadas de un arreglo tan sólo dependen de su poset de intersección. Veremos varias aplicaciones de este teorema. La primera es la generalización de los Teoremas 1.1 y 1.2 a $d$ dimensiones.
Demostración. Esta es una consecuencia inmediata de los Teoremas 3.6 y 3.9.
Vamos a considerar ahora arreglos de hiperplanos sobre otros campos distintos a $\mathbb{R}$. En particular, resulta útil considerar arreglos en un espacio vectorial finito $\mathbb{F}_q^d$, aun si nuestro interés principal son los arreglos reales. Acá $\mathbb{F}_q$ es el campo finito de $q$ elementos, donde $q=p^\alpha$, $p$ es un número primo y $\alpha \in \mathbb{Z}_{>0}$. Algunas nociones como el número de regiones no existen (pues $\mathbb{F}_q$ no es un campo ordenado), pero otras nociones como el poset de intersección permanecen iguales, y permiten darle nuevas interpretaciones al polinomio característico.
Supongamos que $\mathcal{A}$ es un arreglo en $\mathbb{R}^d$ cuyas ecuaciones tienen coeficientes enteros. Utilizando las mismas ecuaciones sobre el campo finito $\mathbb{F}_q$, obtenemos un arreglo $\mathcal{A}_q$ en $\mathbb{F}_q^d$. El siguiente resultado reduce el cálculo del polinomio característico de $\mathcal{A}$ a un problema enumerativo en $\mathbb{F}_q^d$.
Demostración. Cada intersección de hiperplanos $Y\in L(\mathcal{A}_q)$ es un espacio afín de dimensión $k$ y, por lo tanto, tiene $q^k$ elementos. Así, cada sumando $\mu(Y)q^k$ en la definición de $\chi_{\mathcal{A}}(q)$ cuenta el número de puntos de $Y$ multiplicado por $\mu(Y)$. Luego, cada punto $v$ de $\mathbb{F}_q^d$ contribuye a $\chi_{\mathcal{A}}(q)$ un total de $\sum_{Y \, : \, v \in Y}\mu(Y) = \sum_{Y\leq X}\mu(Y)$, donde $X$ es el mínimo elemento de $L(\mathcal{A})$ que contiene a $v$. Esta suma es igual a $0$ si $X \neq \mathbb{F}_q^d\in L(\mathcal{A}_q)$ y es igual a $1$ si $X = \mathbb{F}_q^d$ es el mínimo elemento del poset. Por lo tanto, los únicos puntos que contribuyen son los que no están en ningún hiperplano de $\mathcal{A}$, y $\chi_{\mathcal{A}_q}(q) = | \mathbb{F}_q^d - \mathcal{A}_q|$.
Por último, observamos que cada elemento de $L_{\mathcal{A}}$ es el espacio de soluciones a un sistema de ecuaciones lineales y, si $p$ es suficientemente grande, se tiene que hay un elemento correspondiente de $L_{\mathcal{A}_q}$ que satisface las mismas ecuaciones (en $\mathbb{F}_q$). En ese caso, tendremos que $L_{\mathcal{A}} \cong L_{\mathcal{A}_q}$ y también $\chi_{\mathcal{A}} = \chi_{\mathcal{A}_q}$. El resultado se sigue. ▢
El teorema anterior puede ser de gran ayuda para calcular el polinomio característico de un arreglo, pues en muchos casos es fácil contar los puntos en cuestión en términos de $q$. Con frecuencia nos enfocaremos en el caso en que $q$ es un primo suficientemente grande.
En este caso, el método de los campos finitos nos permite verificar fácilmente que el polinomio característico coincide con el del Ejemplo 3.5. Para apreciar verdaderamente su utilidad, es necesario estudiar ejemplos más interesantes, en los cuales el método de campos finitos puede simplificar increíblemente los cálculos. En la sección siguiente, vamos a ver varios ejemplos importantes.
Este arreglo puede verse como la variedad algebraica $Z(\Delta _n)$, que consiste de los ceros del polinomio de Vandermonde $\prod_{1 \leq i < j \leq n} (x_i-x_j)$. Veamos cómo el método de campos finitos nos permite calcular fácilmente el polinomio característico de este arreglo.
Demostración. Al considerar $\mathcal{B}_n$ sobre el campo finito $\mathbb{F}_q$ para un primo $q$ suficientemente grande, vemos que el número de puntos de $\mathbb{F}_q^n$ que no pertenece a ningún hiperplano está dado por $$q(q-1)(q-2)(q-3)\cdots (q-n+1)=\chi_{\mathcal{B}_n}(q),$$ pues tan sólo debemos escoger como coordenadas $n$ elementos distintos de $\mathbb{F}_q$. Para la primera coordenada, hay $q$ posibilidades; para la siguiente $q-1$ y así sucesivamente. Como esta igualdad es válida para infinitos valores de $q$, debe ser una igualdad de polinomios. ▢
Para el arreglo de trenzas también es posible, pero mucho más difícil, calcular el polinomio característico usando la función de Möbius. Por ejemplo, para $n=4$, el poset de intersección de $\mathcal{B}_4$ se muestra en la Figura 5.
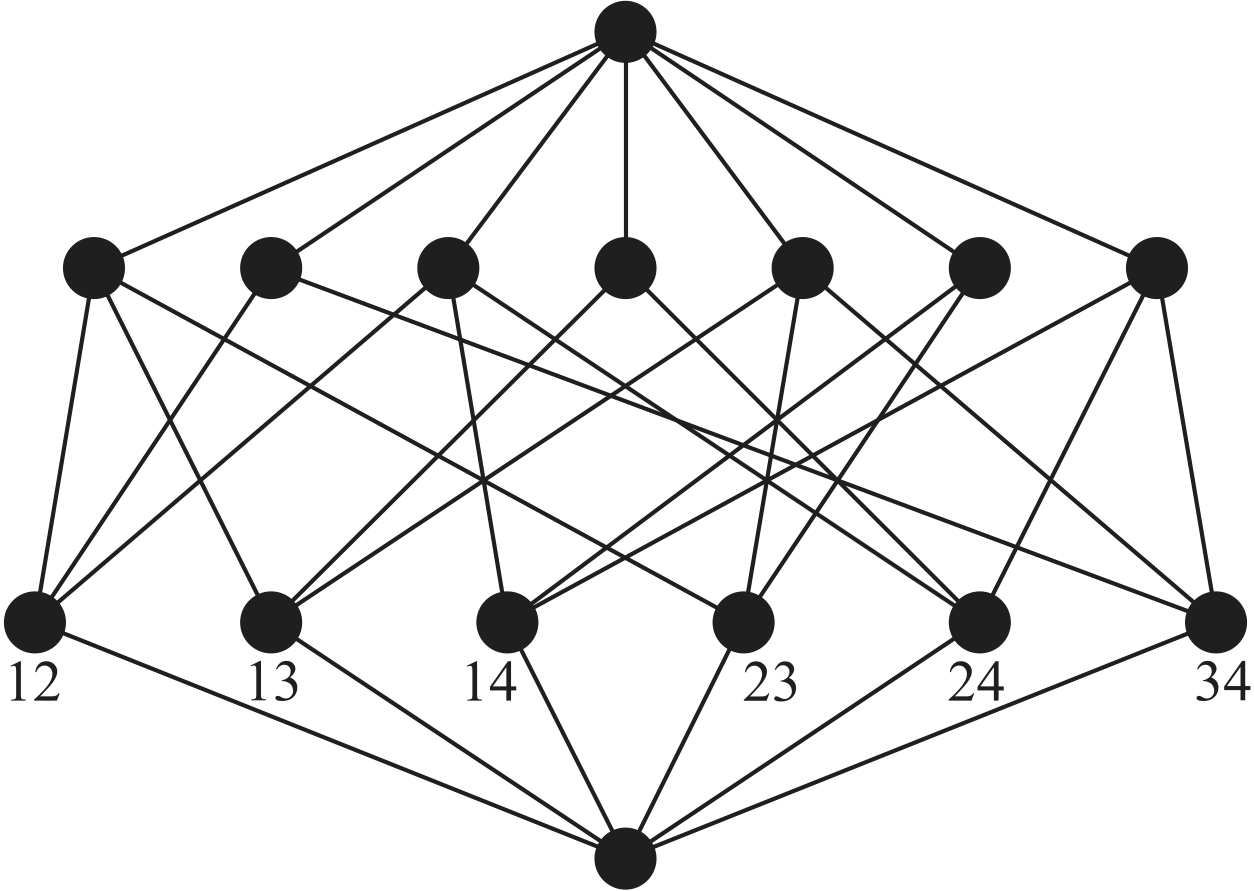
Cada elemento marcado con un par $ij$ representa al hiperplano $x_i=x_j$.
Demostración. Esta es una consecuencia inmediata del Teorema de Zaslavsky (Teorema 3.9) y del Teorema 5.2. Es fácil e ilustrativo dar una prueba directa de estas afirmaciones. La segunda igualdad es clara ya que todos los hiperplanos pasan por el origen. La primera igualdad tiene una sencilla explicación combinatoria. Cada región está dada por un sistema de desigualdades donde, para cada par $i,j$, se elije si $x_i < x_j$ o $x_j < x_i$. Juntando todas las desigualdades, podemos encontrar en qué orden se encuentran todos los $x_i$. Además, cada orden posible de las $n$ coordenadas determina una única región. Así concluimos que las regiones de $\mathcal{B}_n$ están en biyección con las $n!$ permutaciones de $\{1, \ldots, n\}$. ▢
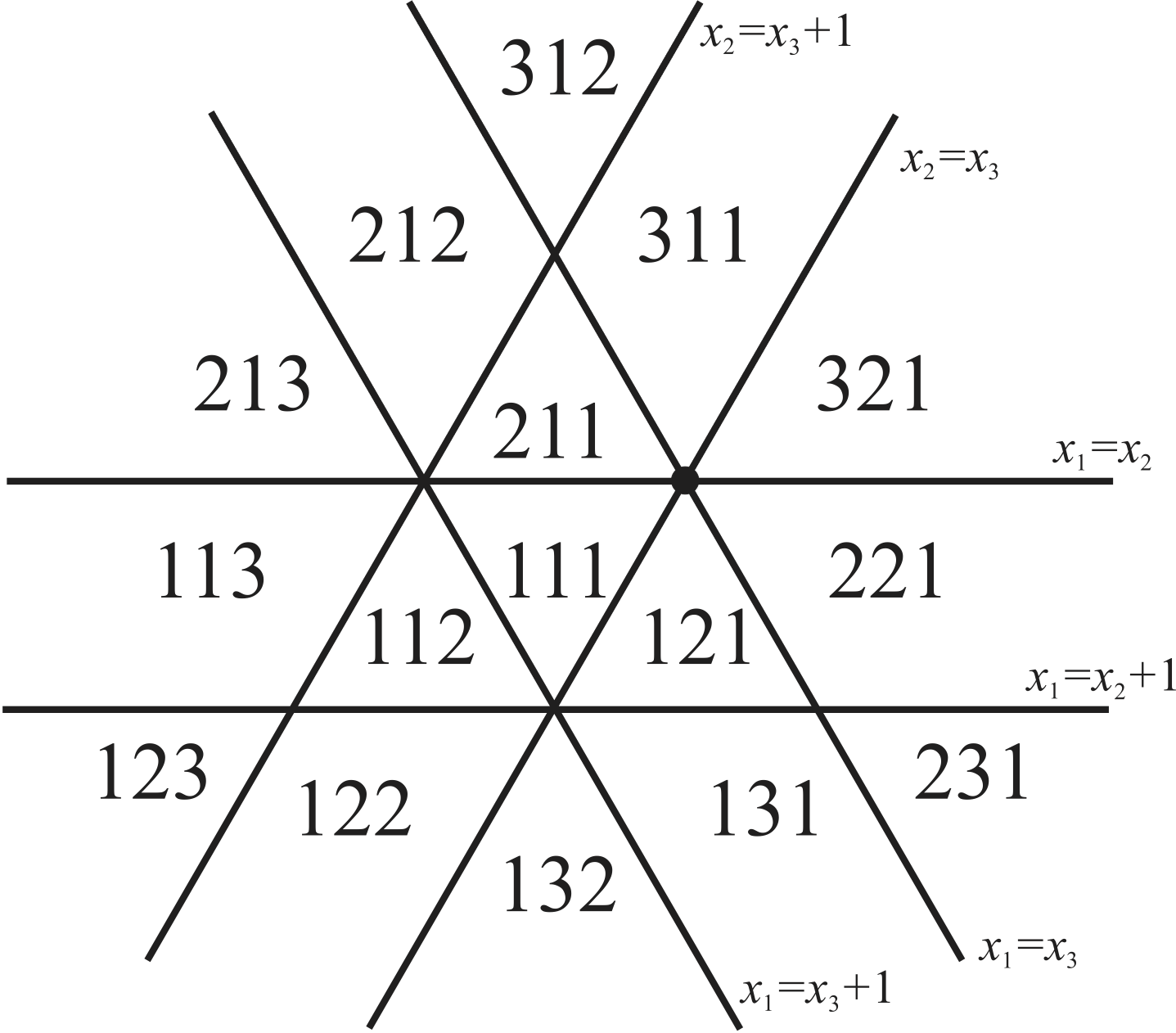
En la Figura 6 se muestran las regiones del arreglo de trenzas para el caso $n=3$.
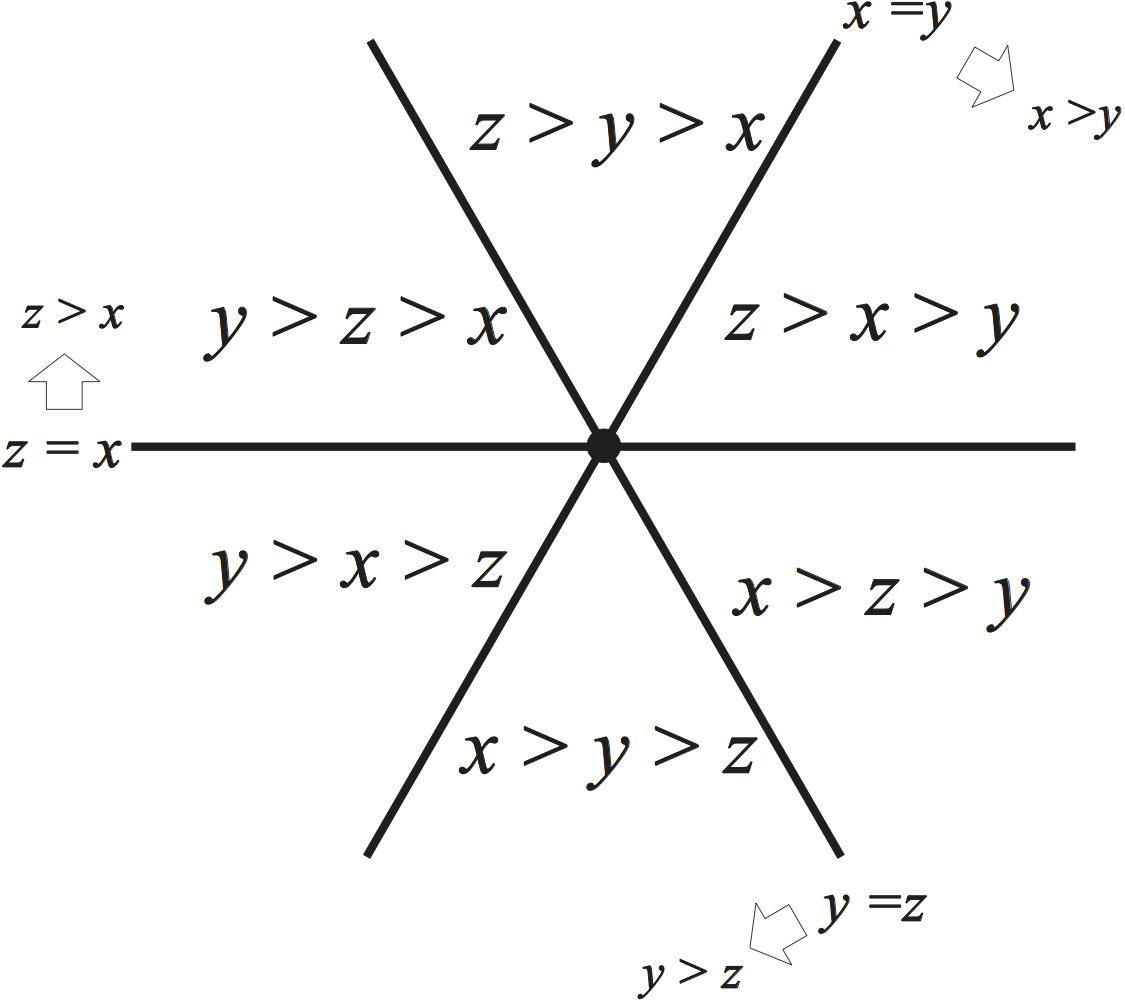
Este es un arreglo en $\mathbb{R}^3;$ pero, como todos los hiperplanos contienen la línea $\mathbb{R}(1,1,1)$, dibujamos su esencialización intersectando el arreglo con el plano $x+y+z=0$.
Un tema clásico de la teoría de grafos es el de las coloraciones propias de un grafo $G$. Éstas son las coloraciones de los vértices del grafo tales que dos vértices unidos por un arco no pueden tener el mismo color. Se puede demostrar que existe un polinomio $\chi_G(x)$, conocido como el polinomio cromático de $G$, con la siguiente propiedad: si tenemos $t$ colores disponibles, el número de coloraciones propias del grafo $G$ es igual a $\chi_G(t)$. Algunas propiedades de estos polinomios se pueden encontrar en [18]R. Stanley, An Introduction to Hyperplane Arrangements. IAS/Park City Mathematics Series, 2005..
Demostración. Considerando el arreglo $\mathcal{A}_G$ sobre el campo finito $\mathbb{F}_q$, vemos que los puntos de $\mathbb{F}_q^n$ que no pertenecen a ninguno de los hiperplanos están en biyección con las coloraciones propias de $G$ con $q$ colores: la $i$-ésima coordenada del punto nos da el color del vértice $i$ en la coloración. Usando el Teorema 4.1, concluimos que $\chi_G(q)=\chi_{\mathcal{A}_G}(q)$ para casi todo primo $q$ y, por lo tanto, $\chi_G=\chi_{\mathcal{A}_G}$ como polinomios. ▢
También es posible dar una interpretación al número de regiones de un arreglo gráfico, con lo cual el polinomio característico contendría aún más información del grafo. Para ver esto, nótese que cada región de un arreglo gráfico $\mathcal{A}_G$ está determinada por un sistema de desigualdades de la forma $x_i < x_j$, para cada pareja de vértices $i,j$ unida por un arco. Estas desigualdades se pueden marcar en el grafo, poniendo en cada arco una flecha de $i$ hasta $j$ si $x_i< x_j$, o viceversa. Así, cada sistema de desigualdades define una orientación de los arcos de $G$, como se muestra en la Figura 7.
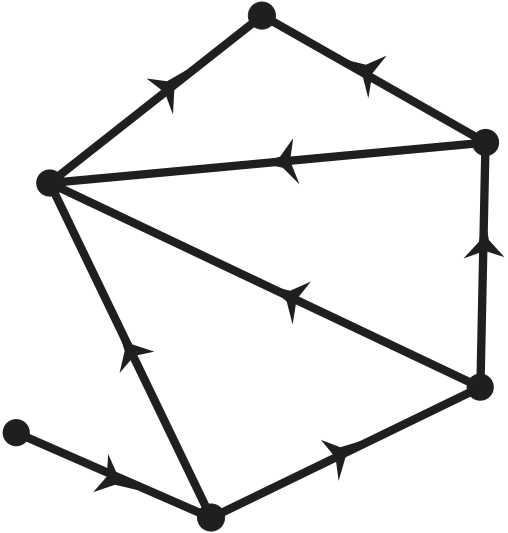
Demostración. Si el sistema de desigualdades tiene solución, el grafo no puede tener ciclos, pues esto implicaría desigualdades de la forma $x_i< x_j< \cdots < x_i$. Por otro lado, dada una orientación acíclica, vamos a mostrar que el sistema de desigualdades correspondiente tiene solución, de forma inductiva sobre el número de vértices $n$. Para $n=1$, el resultado es obvio. Para $n \geq 2$, como el grafo es acíclico, debe haber al menos un vértice $v$ del que no sale ningúna flecha. Podemos entonces retirar a $v$ del grafo, junto con todos los arcos que llegan a $v$. El grafo $G'$ orientado que resulta también es acíclico y con menos vértices que el original. Usando la hipótesis de inducción, es posible construir una solución al sistema correspondiente a $G'$; y dándole a la variable asociada a $v$ un valor menor a todos los demás, obtenemos una solución a nuestro sistema de desigualdades.▢
Demostración. Basta notar que $$\mathrm{r}(\mathcal{A}_G)=(-1)^n\chi_{\mathcal{A}_G}(-1)=(-1)^n\chi_G(-1).$$ y que las orientaciones acíclicas de $G$ están en biyección con las regiones del arreglo $\mathcal{A}_G$. ▢
Es muy interesante que el estudio de arreglos de hiperplanos nos haya permitido demostrar fácilmente este teorema puramente combinatorio.
Volvamos brevemente al tema de la ubicación de los ceros de polinomios combinatorios, que ya apareció en el primero de estos tres artículos. El problema de la ubicación de los ceros de $\chi_G(t)$ ha recibido gran interés, en parte gracias a su relación con el famoso Teorema de los Cuatro Colores. Este teorema dice que cualquier mapa puede ser coloreado con cuatro colores sin que haya dos países vecinos del mismo color. Esta afirmación es equivalente a decir que si $G$ es plano (es decir, que puede pintarse en el plano sin que los arcos se corten), entonces $\chi_G(4)\neq 0.$ Otros resultados conocidos son los siguientes [14]A. Sokal. Bounds on the Complex Zeros of (Di)Chromatic Polynomials and Potts-Model Partition Functions. Combin. Probab. Comput. 10 (2001) 41-77.,[15]A. D. Sokal, Chromatic roots are dense in the whole complex plane. Combin. Probab. Comput. 13 (2004), 221-261.:
Los números de Catalan $C_n$ están dados por la fórmula $$C_n=\frac1{n+1}{2n \choose n},$$ para $n\in\mathbb{N}$.
Los números de Catalan aparecen naturalmente en una gran cantidad de contextos matemáticos. En particular, uno de los ejercicios del libro [17]R. Stanley, Enumerative Combinatorics, vol 2. Cambridge University Press, Cambridge, 1999. contiene cientos de problemas combinatorios cuya respuesta son los números de Catalan. Un ejemplo importante es el siguiente: el número de Catalan $C_n$ es el número de sucesiones de votación $b_1,b_2,\ldots,b_{2n}$ donde cada $b_i$ es $1$ o $-1$, tales que \[ b_1+\cdots+b_i \geq 0 \quad\textrm{ para } i=1, \ldots, 2n-1 \qquad \quad \textrm{y } \qquad \quad b_1+\cdots+b_{2n}= 0. \] El nombre proviene de un modelo de unas elecciones donde $2n$ votantes votan por uno de dos candidatos A y B. Los votos se reciben en orden, y el candidato A nunca está detrás del candidato B, pero al final el resultado es un empate.
Los números de Catalan cumplen la relación de recurrencia \[ C_0=1, \qquad \qquad C_{n+1}=C_0C_n+C_1C_{n-1}+\cdots+C_nC_0 \quad {(n \geq 0)}. \]
Demostración. Usaremos nuevamente el método de campos finitos (Teorema 4.1). Sea $q>2n$ un primo, y encontremos el número de formas de seleccionar $n$ valores $(x_1,x_2,\ldots,x_n)$ en $\mathbb{F}_q^n$, de forma que no haya valores repetidos ni dos valores consecutivos entre las coordenadas. Para el valor de $x_1$ hay $q$ posibilidades. Para escoger los valores que pueden tomar las otras coordenadas $x_i$, hay en total ${q-n-1\choose n-1}(n-1)!$ posibilidades; ya que, si escogemos $n-1$ enteros $z_1< z_2< \cdots< z_{n-1}$ entre $1$ y $q-n-1$, podemos darle a las otras $n-1$ coordenadas de $x$ los valores $x_1+z_1+1, x_1+z_2+2, \ldots,$ y $x_1+z_{n-1}+{n-1}$ en cualquiera de los $(n-1)!$ órdenes posibles. Los $n$ valores que resultan son distintos y no hay dos consecutivos. En la dirección contraria, dado un punto $x$ en $\mathbb{F}_q^n$ que no está en ningún hiperplano, es fácil recuperar los valores de $x_1, z_1, \ldots, z_{n-1}$.
Concluimos entonces que el número de puntos de $\mathbb{F}_q^n$ que no están en ninguno de los hiperplanos de $\mathcal{C}_n$ es $$q{q-n-1\choose n-1}(n-1)!=q(q-n-1)(q-n-2)(q-n-3)\cdots (q-2n+1),$$ y de aquí, el resultado se sigue. ▢
Demostración. Combinando el Teorema de Zaslavsky (Teorema 3.9) con el Teorema 5.10, obtenemos una prueba directa de estos resultados. Vamos a esbozar una segunda demostración que aclara la relación entre los arreglos de Catalan y los números de Catalan. La demostración completa se encuentra, por ejemplo, en [9]E. León, Conteos en Arreglos de Hiperplanos, Números de Catalan y Funciones de parqueo. Universidad Nacional de Colombia, Bogotá, trabajo de grado, 2006..
El arreglo de Catalan contiene al arreglo de trenzas, que divide a $\mathbb{R}^n$ en $n!$ sectores iguales. En cada sector, el orden de las coordenadas de los puntos está dado por una permutación fija. Consideremos, por ejemplo, la región $x_1 > x_2 > \cdots > x_n$ de $\mathcal{B}_n$; vamos a demostrar que el arreglo de Catalan la divide en $C_n$ subregiones. Para especificar una de estas subregiones, debemos decidir si $x_i-x_j < 1$ o $x_i - x_j > 1$ para cada $i< j$ (ya sabemos que $x_i-x_j > -1$ para cada $i< j$.) En otras palabras, debemos decidir el orden de los números $x_1, \ldots, x_n, x_1+1, \ldots, x_n+1$, sabiendo que $x_1> \cdots >x_n$ y $x_1+1 > \cdots > x_n+1$. Para cada orden posible, reemplacemos cada $x_i$ por un $-1$ y cada $x_i+1$ por un $1$. Por ejemplo, el orden $$x_1+1 > x_2+1 > x_1 > x_3+1 > x_2 > x_4+1 > x_3 > x_4$$ se convierte en la sucesión $(1,1,-1,1,-1,1,-1,-1)$. Es claro que el resultado es una sucesión de votación, y cada sucesión de votación corresponde a una subregión. Además, uno puede verificar que la región es acotada cuando todas las sumas parciales $b_1+\cdots + b_j$ con $1 \leq j \leq 2n-1$ son positivas. También es fácil ver que hay exactamente $C_{n-1}$ sucesiones con esa propiedad. Por lo tanto, la región $x_1 > x_2 > \cdots > x_n$ de $\mathcal{B}_n$ contiene $C_n$ regiones de $\mathcal{C}_n$, de las cuales $C_{n-1}$ son acotadas. El resultado se sigue. ▢
Demostración. Nuevamente, vamos a usar el método de campos finitos; contemos los puntos de $\mathbb{F}_q^n$ que no satisfacen ninguna de las ecuaciones del arreglo de Shi. Representemos a cada uno de esos puntos $x=(x_1, \ldots, x_n)$ por una $q$-tupla $x^{-1}=(y_0, \ldots, y_{q-1})$ de números y símbolos $\circ$, donde $y_i=\circ$ si no existe ningún $j \in [n]$ tal que $x_j=i$, y $y_i = j$ si $j$ es el elemento de $[n]$ tal que $x_j=i$. Tal elemento debe ser único ya que $x$ no tiene valores repetidos. Por ejemplo, al punto $x=(3,2,8,1,5,7,12,11) \in \mathbb{F}_{13}^8$ le corresponde la $13$-tupla $x^{-1} = (\circ, 4, 2, 1, \circ, 5, \circ, 6, 3, \circ, \circ, 8, 7)$. Observemos que cada sucesión de números entre dos $\circ$ consecutivos es decreciente, ya que $x_i-x_j \neq 1$ para $i< j$.
Podemos construir estas $q$-tuplas de una manera alternativa que nos permitirá contarlas fácilmente. Para hacerlo, pensamos en la $q$-tupla $x^{-1}$ como un vector escrito alrededor de un círculo, reflejando la estructura cíclica del campo $\mathbb{F}_q$ bajo adición. Primero, dibujamos $q-n$ símbolos indistinguibles $\circ$. Luego, ubicamos un $1$ entre cualesquiera dos de ellos, teniendo en cuenta que los símbolos $\circ$ son indistinguibles por el momento. Después, ubicamos cada uno de los números $2, \ldots, n$ en alguno de los $q-n$ espacios entre dos $\circ$ consecutivos; esto lo podemos hacer de $(q-n)^{n-1}$ maneras. Si un espacio entre dos $\circ$ consecutivos contiene varios números, los ubicamos en orden decreciente en el sentido de las manecillas del reloj. Esto determina el orden cíclico de los símbolos de la $q$-tupla. Por último, para determinar la $q$-tupla exactamente, necesitamos pasar del orden cíclico a un orden lineal, eligiendo la posición del $1$ en la $q$-tupla, es decir, el valor de $x_1$. Esto nos da un total de $q(q-n)^{n-1}$ posibilidades. Es fácil verificar que este procedimiento produce precisamente los puntos de $\mathbb{F}_q^n$ que no están en ningún hiperplano del arreglo de Shi $\mathcal{S}_n$. ▢
Demostración. Esta es una consecuencia inmediata de la Proposición 5.13 y el Teorema de Zaslavsky. ▢
El arreglo de Shi está cercanamente relacionado a ciertas listas de números conocidas como funciones de parqueo. Para explicar su definición, consideremos la siguiente situación.
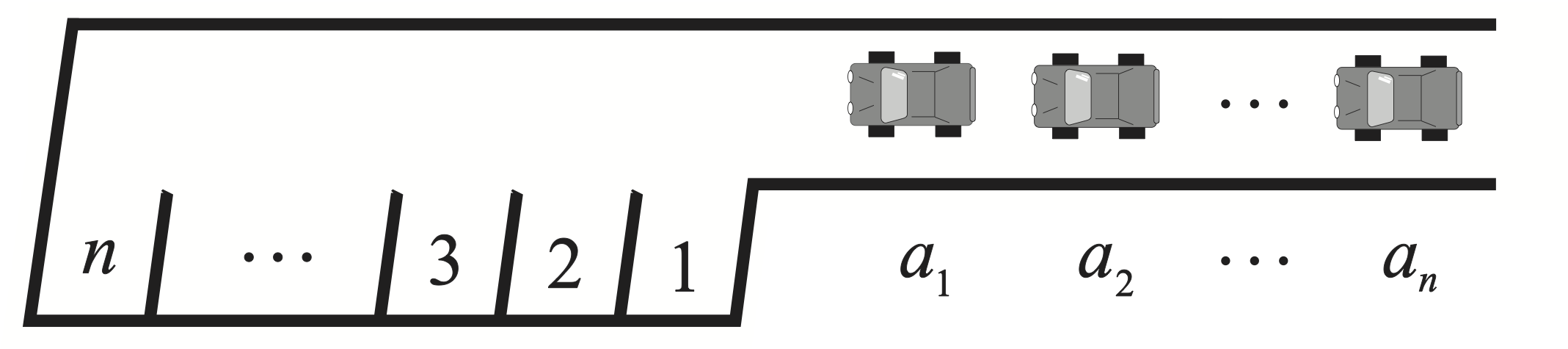
En un parqueadero se tienen $n$ espacios ubicados en línea, numerados en orden de $1$ a $n$, donde el espacio número $1$ es el más cercano a la puerta de entrada del parqueadero, y el número $n$ se encuentra llegando a la salida. Una fila de $n$ autos se dispone a entrar al parqueadero. Cada uno de los conductores tiene un sitio preferido que desea utilizar. Es posible representar todas las elecciones de los autos mediante una lista de números $(a_1,a_2,\ldots,a_n)$, donde el auto $i$ escoge el lugar $a_i$. Es posible que varios autos tengan el mismo espacio preferido; es decir, que $a_i = a_j$ para $i \neq j$.
Una vez que van llegando los autos en orden, cada uno de ellos se dirige al sitio que escogió. Si el espacio está vacío, el auto se estaciona en ese lugar. En caso contrario, el auto sigue andando y se ubica en el primer lugar vacío que encuentra. Si ninguno de los lugares siguientes está libre, el auto no podrá estacionarse.
Konheim y Weiss [7]A. G. Konheim y B. Weiss, An occupancy discipline and applications. SIAM J. Applied Math. 14 (1966) 1266-1274. demostraron los siguientes dos teoremas:
Es posible demostrar el Teorema 5.18 por medio de los arreglos de hiperplanos gracias a la cercana relación entre las funciones de parqueo y el arreglo de Shi. Teniendo en cuenta el Corolario 5.14 es suficiente dar una biyección entre las funciones de parqueo de longitud $n$ y las regiones del arreglo de Shi $\mathcal{S}_n$. A continuación, vamos a describir una biyección $\lambda$. La Figura 9 ilustra esta biyección para $n=3$.
Para definir la biyección $\lambda$, comenzaremos por llamar $R_0$ a la ``región base", en la cual $x_1 < x_2 < \cdots < x_n < x_1+1 < x_2+1 < \cdots < x_n+1$. Dadas dos regiones $R$ y $R'$, definimos la distancia $d(R,R')$ como el número de hiperplanos $H$ del arreglo tales que $R$ y $R'$ se encuentran a lados opuestos de $H$; es decir, el número de hiperplanos que debemos cruzar para llegar de $R$ a $R'$. Construimos entonces la función $\lambda(R)$ recursivamente en función de $d(R_0,R)$ de la siguiente manera:
Es fácil ver que la función $\lambda$ está bien definida. También es cierto (pero no es tan fácil verlo) que es una biyección entre las regiones de $\mathcal{S}_n$ y las funciones de parqueo de longitud $n$.
La construcción de esta biyección $\lambda$ se debe a Igor Pak, y puede ser extendida a las $k$-funciones de parqueo que están relacionadas con los arreglos de $k$-Shi $\mathcal{S}_n^k$. No entraremos en detalle al respecto, pero la demostración de la biyección de Pak y su generalización a los arreglos de $k$-Shi puede encontrarse en [19]R. Stanley. Hyperplane arrangements, parking functions, and tree inversions, in Mathematical Essays in Honor of Gian-Carlo Rota (B. Sagan and R. Stanley, eds.) Birkhäuser, Boston/Basel/Berlin, 1998, pp. 259-375..
El número $(n+1)^{n-1}$ juega un papel importante en varios contextos combinatorios. Tal vez el más importante es que cuenta el número de árboles númerados $0, \ldots, n$. Una inversión en un árbol es un par de vértices $i,j$ con $1\leq i < j\leq n$ tal que $j$ se encuentra en el camino de $i$ hasta 0. Kreweras [8]G. Kreweras, Une famille de polynômes ayant plusieurs propriétés énumeratives, Periodica Mathematica Hungarica 11(4), 1980. construyó una biyección entre las funciones de parqueo y los árboles numerados que demuestra el siguiente resultado:
El siguiente arreglo es parecido a los anteriores, aunque el cálculo de su polinomio característico y su número de regiones, debidos a Alex Postnikov [12]A. Postnikov y R. Stanley, Deformation of Coxeter Hyperplane Arrangements Massachusetts Institute of technology, Cambridge, MA 02139, 1997., es más sutil.
Un árbol alternante es un árbol cuyos vértices están numerados $1, 2, \ldots, n$ de manera que todo vértice es, o bien mayor que todos sus vecinos, o bien menor que todos ellos.
Se conocen varias familias de objetos que están en biyección con los árboles alternantes. Sin embargo, aún no se conoce una biyección natural entre las regiones de $\mathcal{L}_n$ y los árboles alternantes. Tampoco se conoce una interpretación de las regiones acotadas del arreglo de Linial, en términos de árboles alternantes u otros objetos combinatorios. También sería interesante encontrar una interpretación combinatoria para los coeficientes del polinomio $\chi_{\mathcal{L}_n}(t)$. Culminamos esta sección con un resultado muy sorprendente, la "hipótesis de Riemann para el arreglo de Linial":
En esta sección, consideramos los arreglos de hiperplanos sobre el campo $\mathbb{C}$ de los números complejos. Los complejos no forman un campo ordenado, por lo cual un hiperplano en $\mathbb{C}^d$ no tiene un lado `positivo' y otro `negativo'. Por el contrario, el complemento de un hiperplano es un espacio conexo. Por lo tanto, no es posible definir regiones como lo hicimos sobre los reales. Ahora la topología del complemento $\mathbb{C}^d - \mathcal{A}$ del arreglo es más complicada, pero aún guarda una estrecha relación con el poset de intersección y el polinomio característico que se pueden definir igual que antes.
Sea $\mathcal{A}=\{H_1, \ldots, H_n\}$ un arreglo de hiperplanos en $\mathbb{C}^d$. Sea $E(\mathcal{A})$ el álgebra asociativa sobre $\mathbb{C}$ generada por los hiperplanos (considerados como símbolos formales), sujeta únicamente a las relaciones $H_i^2=0$ para $1 \leq i \leq n$ y $H_iH_j=-H_jH_i$ para $1 \leq i < j \leq n$. Es claro que $\{\prod_{H \in \mathcal{B}} H \, : \, \mathcal{B} \subseteq \mathcal{A}\}$ es una base de $E(\mathcal{A})$ como espacio vectorial y, por lo tanto $\dim(E(\mathcal{A})) = 2^n$ (algunos lectores reconocerán $E(\mathcal{A})$ como el álgebra exterior de un espacio vectorial de dimensión $n$.)
Definimos la función lineal $\partial:E(\mathcal{A}) \rightarrow E(\mathcal{A})$ de la siguiente manera \[ \partial(H_{i_1}H_{i_2}\cdots H_{i_k}) = \sum_{j=1}^k (-1)^j H_{i_1} \cdots \widehat{H_{i_j}} \cdots H_{i_k} \] donde $\widehat{H_{i_j}}$ significa que omitimos el término $H_{i_j}$. Decimos que $H_{i_1}, \ldots, H_{i_k}$ son dependientes si sus vectores normales lo son; es decir, si $\dim(H_{i_1} \cap \cdots \cap H_{i_k}) > d-k$.
Sea $I_{\mathcal{A}}$ el ideal de $E(\mathcal{A})$ generado por \\ $\bullet$ Los productos $H_{i_1}H_{i_2}\ldots H_{i_k}$ tales que $H_{i_1}\cap H_{i_2}\cap\ldots \cap H_{i_k}=\emptyset$, y\\ $\bullet$ Los elementos $\partial(H_{i_1}H_{i_2}\ldots H_{i_k})$ tales que $H_{i_1}, \ldots, H_{i_k}$ son dependientes.
Podemos considerar a $E(A) = E(\mathcal{A})_0 \oplus E(\mathcal{A})_1 \oplus \cdots \oplus E(\mathcal{A})_n$ como un espacio vectorial graduado donde la componente $E(\mathcal{A})_k$ de grado $k$ es generada por los productos $H_{i_1}\cdots H_{i_k}$ de grado $k$. Como $I_{\mathcal{A}}$ es un ideal homogéneo, el cociente $OS(\mathcal{A}) = OS(\mathcal{A})_0 \oplus \cdots \oplus OS(\mathcal{A})_n$ también es graduado.
Sea $\mathcal{A}$ el arreglo en $\mathbb{C}^2$ cuyos hiperplanos son $x=0, \, y=0,\, x+y=0,$ y $x-y=1$. En la Figura 10, ilustramos la parte real de este arreglo. El lector puede calcular fácilmente el poset de intersección (que es igual si consideramos el arreglo en $\mathbb{C}^2$ o en $\mathbb{R}^2$), la función de Möbius, y el polinomio característico de $\mathcal{A}$, que es $\chi_\mathcal{A}(t) = t^2-4t+5$.
Ahora, $E(\mathcal{A})$ es generado por variables no conmutativas $a,b,c,d$ sujetas a las relaciones \[ a^2=b^2=c^2=d^2=0, \qquad ab=-ba, \, ac=-ca, \, \ldots,\, cd=-dc. \] El álgebra de Orlik-Solomon $OS(\mathcal{A})$ se obtiene al introducir las relaciones adicionales \[ abd=acd=bcd=0, \qquad -bc+ac-ab=0. \] De ahí vemos que la siguiente es una base para $OS(\mathcal{A})$ como espacio vectorial: \[ \{1, \,\,\,\, a, b, c, d, \,\,\,\, ab, ac, ad, bd, cd\}. \] No incluimos al monomio $bc$ en la base porque $bc=ac-ab$. Tampoco incluimos a $abc$ porque en $OS(\mathcal{A})$ se tiene que $abc=a(ac-ab) = a^2(c-b)=0$. Tenemos entonces que \[ \text{Hilb}_{OS(\mathcal{A})}(x)=1+4x+5x^2. \]
Algunos lectores reconocerán alguna semejanza entre la Definición 6.1 y algunas construcciones en la topología algebraica. De hecho, la gran importancia del álgebra de Orlik-Solomon se debe a los siguientes elegantísimos resultados:
No daremos una definición precisa de la cohomología de de Rham y los números de Betti en estas notas, cuyo enfoque es combinatorio. Para ver una descripción completa, referimos al lector a [5]R. Bott y L. Tu. Differential Forms in Algebraic Topology, Berlin, New York: Springer-Verlag. 1982., o a [11]P. Orlik y H. Terao, Arrangements of Hyperplanes, Springer-Verlag, Berlin, 1992. para una presentación desde el punto de vista de los arreglos de hiperplanos. Nos limitaremos a mencionar que, como dijimos anteriormente, \textbf{en un espacio real $\mathbb{R}^d$}, el complemento de un arreglo $\mathcal{A}$ es una unión disjunta de regiones contráctiles. Topológicamente, es un espacio bastante trivial. Su única característica interesante es el número de regiones $\mathrm{r}(\mathcal{A})$, que ya sabemos calcular combinatoriamente. Por el contrario, \textbf{en un espacio complejo} $\mathbb{C}^d$, la topología del complemento $\mathbb{C}^d-\mathcal{A}$ es más interesante. Por ejemplo, vemos que éste es un espacio conexo, ya que podemos dar una vuelta alrededor de cada hiperplano. La cohomología del complemento es un anillo graduado que ``mide" de cierta manera la topología de este espacio. El $i$-ésimo número de Betti $\beta_i = \dim H^i_{DR}(\mathbb{C}^d - \mathcal{A}, \mathbb{C})$ nos dice cuántos huecos $i$-dimensionales independientes tiene este espacio. Es de gran interés que Orlik y Solomon hayan logrado dar una presentación puramente combinatoria de la cohomología de este espacio y su polinomio de Hilbert.
En resumen, el polinomio característico $\chi_\mathcal{A}(x)$ de un arreglo de hiperplanos $\mathcal{A}$ es un poderoso invariante combinatorio, que contiene una gran cantidad de información sobre el arreglo:
Éste es tan sólo el comienzo de la teoría de arreglos de hiperplanos. Invitamos al lector a seguir profundizando en esta fascinante área.
Agradecemos muy especialmente a Richard Stanley, de quien aprendimos la teoría combinatoria de arreglos de hiperplanos. A esto se debe que esta lección, escrita originalmente en 2003, tiene bastante en común con sus notas [18]R. Stanley, An Introduction to Hyperplane Arrangements. IAS/Park City Mathematics Series, 2005. de 2005.
[1] F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. I. Matrices totalmente no negativas y funciones simétricas. universo.math, 1 no.1 (2014) artículo 5.
[2] F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. II. Las funciones simétricas y la teoría de las representaciones. universo.math, 1 no.2 (2014) artículo 5.
[3] F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. III. Arreglos de hiperplanos, universo.math, 1 no.3 (2014).
[4] C. A. Athanasiadis. Characteristic polynomials of subspace arrangements and finite fields, Advances in Math. 122 (1996), 193-233.
[5] R. Bott y L. Tu. Differential Forms in Algebraic Topology, Berlin, New York: Springer-Verlag. 1982.
[6] H. Crapo y G.-C. Rota. On the Foundations of Combinatorial Theory: Combinatorial Geometries. MIT Press, Cambridge, MA, 1970.
[7] A. G. Konheim y B. Weiss, An occupancy discipline and applications. SIAM J. Applied Math. 14 (1966) 1266-1274.
[8] G. Kreweras, Une famille de polynômes ayant plusieurs propriétés énumeratives, Periodica Mathematica Hungarica 11(4), 1980.
[9] E. León, Conteos en Arreglos de Hiperplanos, Números de Catalan y Funciones de parqueo. Universidad Nacional de Colombia, Bogotá, trabajo de grado, 2006.
[10] P. Orlik y L. Solomon, Combinatorics and topology of complements of hyperplanes. Invent. Math. 56 (1980) 167-189.
[11] P. Orlik y H. Terao, Arrangements of Hyperplanes, Springer-Verlag, Berlin, 1992.
[12] A. Postnikov y R. Stanley, Deformation of Coxeter Hyperplane Arrangements Massachusetts Institute of technology, Cambridge, MA 02139, 1997.
[13] G. C. Rota. On the Foundations of Combinatorial Theory I: Theory of Möbius Functions. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete, 2 (1964) 340-368.
[14] A. Sokal. Bounds on the Complex Zeros of (Di)Chromatic Polynomials and Potts-Model Partition Functions. Combin. Probab. Comput. 10 (2001) 41-77.
[15] A. D. Sokal, Chromatic roots are dense in the whole complex plane. Combin. Probab. Comput. 13 (2004), 221-261.
[16] R. Stanley, Enumerative Combinatorics, vol 1. Wadsworth & Brooks Cole, Belmont, CA, 1986.
[17] R. Stanley, Enumerative Combinatorics, vol 2. Cambridge University Press, Cambridge, 1999.
[18] R. Stanley, An Introduction to Hyperplane Arrangements. IAS/Park City Mathematics Series, 2005.
[19] R. Stanley. Hyperplane arrangements, parking functions, and tree inversions, in Mathematical Essays in Honor of Gian-Carlo Rota (B. Sagan and R. Stanley, eds.) Birkhäuser, Boston/Basel/Berlin, 1998, pp. 259-375.
[20] R. Stanley, Hyperplane arrangements, interval orders, and trees. Proc. Nat. Acad. Sci. 93 (1996), 2620-2625.
[21] T. Zaslavsky, Facing up to Arrangements: Face-Count Formulas for Partitions of Space by Hyperplanes, Thesis (MIT, 1974) and Mem. Amer. Math. Soc., No. 154, Amer. Math. Soc., Providence, R.I., 1975.



