

En marzo de 2003 se llevó a cabo el Primer Encuentro Colombiano de Combinatoria en Bogotá, Colombia. Como parte del encuentro, se organizaron tres minicursos, dictados por Federico Ardila, Mercedes Rosas, y Mark Skandera. Esta serie resume el material presentado en estos cursos en tres artículos: I. Matrices totalmente no negativas y funciones simétricas [1]F. Ardila, E. León, M. Rosas, and M. Skandera, Tres lecciones en combinatoria algebraica. I. Matrices totalmente no negativas y funciones simétricas, universo.math, vol. 1 no. 1 (2014) artículo 5., II. Las funciones simétricas y la teoria de las representaciones [2]lo estás leyendo, y III. Arreglos de hiperplanos [3]F. Ardila, E. León, M. Rosas, and M. Skandera, Tres lecciones en combinatoria algebraica. 3. Aspectos combinatorios de los arreglos de hiperplanos, universo.math, por aparecer..
En esta segunda lección hablaremos sobre nuestra introducción a la teoría de representaciones del grupo simétrico, del grupo lineal general, y a la teoría de las funciones simétricas. Esperamos que este trabajo haga justicia a la experiencia vivida en esos días.
Empezamos por introducir algunas nociones básicas de combinatoria algebraica.
Una sucesión debilmente decreciente de enteros no negativos se denomina partición y se escribe como $ \lambda = (\lambda_1, \lambda_2, \dotsc).$ Un ejemplo de partición es la siguiente: $$\lambda=(7,7,4,1,1,1,0,0).$$ Aquellos $\lambda_i$ mayores que cero se llaman las partes de $\lambda$, y decimos que dos particiones son iguales si difieren solamente en el número de ceros.
El número de partes de $\lambda$ se denomina la longitud de $\lambda$ y se denota por $\ell(\lambda)$. En ocasiones escribimos la partición $\lambda$ describiendo la multiplicidad de sus partes. Así, para nuestro ejemplo, escribimos $\lambda=(1^3\, 4\, 7^2).$
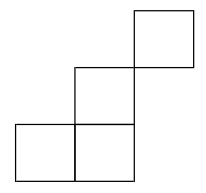
Decimos que $\lambda$ es una partición de $n$ si $ \lambda_1 + \cdots + \lambda_{\ell(\lambda)} = n,. $ En este caso, escribimos $\lambda \vdash n$, o $|\lambda| = n$. Identificamos una partición de $n$ con su diagrama de Young, un arreglo de filas de cuadrados justificados a la izquierda, donde la $i$-ésima fila contiene $\lambda_i$ cuadrados, tal y como se ilustra en la Figura 1. La partición transpuesta de $\lambda$ se define a través de su diagrama de Young, que se obtiene al reflejar el diagrama de $\lambda$ sobre su diagonal principal. Se denota por $\lambda'$.
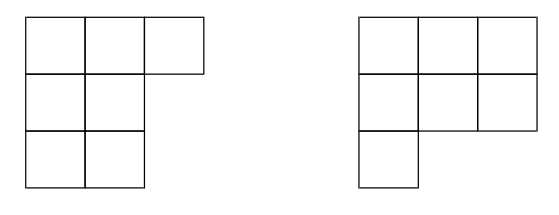
Similarmente, dadas dos particiones $\mu$ y $\lambda$, cuyas diagramas de Young satisfacen que $\mu \subseteq \lambda$, definimos el tablero de Young sesgado, $\lambda / \mu$ como aquél que se obtiene al restar al diagrama de $\lambda$ el diagrama de $\mu$ (vistos como conjuntos).
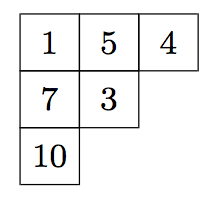
Sea $\lambda$ una partición de $n$, un tableau es una manera de asignar un número natural a cada celda del diagrama de $\lambda$, donde es posible utilizar el mismo número repetidamente. En algunas ocasiones, es conveniente pedir que todas las entradas utilizadas pertenezcan a $[n]$ para algún $n$, donde $[n]$ denota al conjunto $\{1,2,\cdots,n\}$.
Un tableau es semi-estándar si sus columnas crecen estrictamente, mientras que sus filas crecen débilmente. La sucesión \[ (\alpha_1(T), \alpha_2(T), \cdots, \alpha_{n_{\ell}}(T)) \] donde $\alpha_i(T)$ es el número de veces que aparece el número $i$ en el tableau $T$ se denomina el contenido de $T$. Un tableau semi-estándar es estándar si cada uno de los números en $[n]$ aparece exactamente una vez.
Sea $T$ un tableau de forma $\lambda$. El peso de $T$, que denotamos por $x^T$ se define como \[ x^{T}=x_1^{\alpha_1(T)}x_2^{\alpha_2(T)}\ldots \]
El coeficiente de Kostka $K_{\lambda, \mu}$ se define como el número de tableaux semi-estándar de forma $\lambda$ y contenido $\mu$. En particular, denotamos por $f^{\lambda}$ al número de tableaux estándar de forma $\lambda$. Esto es, $\, f^{\lambda}=K_{\lambda,(1^n)}$.

Sean $\mu$ y $\nu$ dos particiones del mismo entero. Definimos al orden de dominancia, denotado por $\unrhd$, diciendo que $\mu \unrhd \nu$ si para cada $k$ tenemos que \[ \mu_1+\mu_2+\cdots+\mu_k \ge \lambda_1+\lambda_2+\cdots+\lambda_k \] En física, este orden se conoce como mayorización.
Trabajaremos siempre sobre el cuerpo de los números complejos. Recordemos que el grupo simétrico $\mathbb{S}_n$ consiste de todas las permutaciones del conjunto $[n]$, junto con la operación de composición. A los elementos del grupo simétrico los denominamos permutaciones. Denotamos por $\pi \sigma$ la permutación obtenida al aplicar primero $\sigma$ y luego $\pi$ a los elementos de $[n]$. A la permutación identidad la denotamos con la letra $\epsilon$.
Utilizamos dos maneras diferentes para denotar permutaciones. De acuerdo con la primera convención, la permutación $\pi$ que envía el número $i$ en $\pi(i)$ la denotamos con la palabra $\pi(1) \, \pi(2) \, \cdots \pi{(n)} $. De acuerdo a la segunda, escribimos $\pi$ como el producto de sus ciclos. Por ejemplo, la permutación $\pi$ definida por $\pi(1)=2,$ $\pi(2)=3,$ $\pi(3)=7,$ $\pi(4)=4,$ $\pi(5)=1,$ $\pi(6)=8,$ $\pi(7)=5,$ $\pi(8)=6$ se escribe, utilizando la primera convención, por la palabra $2 \, 3 \,7 \,4 \,1 \, 8 \, 5 \, 6$. Su descomposición en ciclos es: $(1\, 2 \, 3 \, 7 \, 5 ) (4) (6 \, 8)$. El tipo de una permutación es la partición definida por las longitudes de los ciclos que aparecen en ella. La permutación $\pi$ que aparece en nuestro ejemplo tiene tipo $5 2 1 \vdash 8$.
A cada partición $\lambda$ le asociamos el entero $z_{\lambda}$ definido como \[ z_{\lambda} = 1^{m_1} m_1!\, 2^{m_2} m_2! \, \cdots n^{m_n} m_n!. \]
Comenzamos con una breve exposición de la teoría general de representaciones de grupos, centrándonos en el caso del grupo simétrico y basada en los trabajos de François Bergeron [4]François Bergeron, Combinatoire algebrique, LaCIM, Universite de Quebec á Montreal. versión de 8 avril, 2001., William Fulton [5]W. Fulton, Young tableaux. With applications to representation theory and geometry. London Mathematical Society Student Texts, 35. Cambridge University Press, Cambridge, 1997. y Bruce Sagan [6]Bruce E. Sagan, The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Second edition. Graduate Texts in Mathematics, 203. Springer-Verlag, New York, 2001..
Sea $G$ un grupo, una representación (matricial, compleja) de $G$ es un homomorfismo de grupos entre $G$ y el grupo de las matrices invertibles de orden dado, $GL_d=GL_d(\mathbb C)$. Esto es, \begin{align*} X : G &\rightarrow GL_d\\ \pi &\mapsto X(\pi). \end{align*} Al parámetro $d$ lo llamamos orden o dimensión de la representación. Dada una representación matricial $X$, denotamos $X(\pi) \vec v$ por $\pi \cdot \vec v$. En esta situación decimos que $G$ actúa (linealmente) sobre ${\mathbb{C}}^d$.
Consideramos ahora dos acciones del grupo simétrico sobre $[m]^n$: \begin{align*} \sigma \cdot (v_1, v_2, \cdots, v_n) & = (\sigma(v_1), \sigma(v_2), \cdots, \sigma(v_n)), &&\text{$\sigma \in {\mathbb{S}}_m$ permuta las entradas de $v$.}\\ (v_1, v_2, \cdots, v_n) \cdot \tau &= (v_{\tau(1)},v_{\tau(2)}, \cdots, v_{\tau(n)}), &&\text{$\tau \in {\mathbb{S}}_n$ permuta las posiciones en $v$.} \end{align*}
Dos ejemplos de representaciones del grupo simétrico son la representación trivial, que se obtiene al enviar todos los elementos de ${\mathbb{S}}_n$ a la matriz identidad, y la representación alternante definida por $X(\pi)= ({\rm sgn} (\pi))$. Ambas representaciones tienen orden uno.
Otras dos representaciones del grupo simétrico particularmente importantes son la representación definición, obtenida al hacer actuar ${\mathbb{S}}_n$ sobre el conjunto $[n]$ de la manera canónica (utilizando como base a los elementos de $[n]$), y la representación regular, que proviene de hacer actuar un grupo finito $G$ sobre sí mismo (utilizando como base a los elementos de $G$).
Un homomorfismo de representaciones es una transformación lineal $Y : \mathbb{C}^m \to \mathbb{C}^d$ tal que $Y(g v) = g Y(v)$ para todo $g \in G$ y $v \in \mathbb{C}^m$. Si $Y$ es invertible tenemos entonces un isomorfismo.
En general, decimos que una representación de un grupo finito $G$ es una representación por permutaciones cuando proviene de la acción de $G$ sobre un conjunto finito permutando sus elementos. Esta acción nos proporciona un homomorfismo natural de $G$ al grupo de las matrices de permutación, un interesante subgrupo de $GL_d$. Las matrices correspondientes a representaciones por permutaciones son matrices de permutaciones (matrices en las que cada fila y cada columna contiene exactamente una entrada diferente de cero e igual a uno). Tanto la representación definición como la representación regular son ejemplos de representaciones por permutaciones. Por otra parte, la representación alternante no lo es.
Las representaciones por permutaciones son particularmente interesantes desde un punto de vista combinatorio. Por ejemplo, la traza de $ X(\pi)$ cuenta el número de elementos del conjunto que permanecen fijos bajo la acción de $X$. En particular, el orden (o dimensión) de una representación por permutaciones $X$ viene dado por la traza de $X(\epsilon)$.
El ejemplo con el que concluimos la sección anterior nos sugiere la importancia de considerar la traza de una representación, y nos pone en contacto con un invariante fundamental de cualquier representación de order finito de un grupo.
El carácter de una representación no depende de la base utilizada para construir la matriz asociada a la transformación lineal. Por otra parte, no es necesario que el grupo sea finito para la definición de carácter.
Por ejemplo, el carácter de la representación definición de ${\mathbb{S}}_3$, se calcula rápidamente a partir de los resultados obtenidos en el Ejercicio 2.2. \begin{align*} &&\chi_{def}(123)=3 &&\chi_{def}(213)=1 &&\chi_{def}(321)=1\\ &&\chi_{def}(132)=1 &&\chi_{def}(231)=0 &&\chi_{def}(312)=0 \end{align*} Sabemos que la dimensión de la representación definición viene dada por el valor de su carácter en la identidad. Más generalmente, tenemos que $\chi_{def}(\sigma)$ cuenta el número de puntos fijos de $\sigma$.
Los caracteres juegan un rol fundamental en la teoría de representaciones de los grupos finitos. Esto se debe al siguiente resultado que nos dice que, no solamente son un invariante dentro de sus clases de isomorfismos, sino que nos permite distinguirlas.
Pronto volveremos a la noción de carácter. Ahora nos planteamos el problema de descomponer una representación $X : G \to GL_d(\mathbb{C})$ como una suma directa de representaciones más sencillas. Empezamos por estudiar los subespacios de $\mathbb{C}^d$ que permanecen invariantes bajo $G$.
Por ejemplo, el subespacio generado por $W=\vec 1 + \vec 2 + \vec 3$ es invariante bajo la representación definición de ${\mathbb{S}}_3$.
El complemento ortogonal de un subespacio $G$-invariante $W$ también es invariante, siempre y cuando el producto escalar que lo define sea invariante bajo $G$, es decir $\langle u, v \, \rangle = \langle g \cdot u, g \cdot v \, \rangle $ para todo $u, v \in V$ y $g \in G$. Para la representación definición de $\mathbb{S}_n$, el producto escalar canónico es invariante. (Precisamente, es él que hace que los vectores de la base canónica sean ortonormales). Tenemos entonces que el complemento ortogonal al subespacio $W=\vec 1 + \vec 2 + \vec 3$ también es invariante por la representación definición de ${\mathbb{S}}_3$. Este espacio está generado por $\vec 2 - \vec 1$ y $\vec 3 - \vec 1$.
La representación definición de ${\mathbb{S}}_n$ actúa de manera trivial sobre el subespacio generado por $1+2+\ldots+n$. La restricción de esta representación al complemento ortogonal de este subespacio lo denominamos la representación estándar. Tiene por base $\vec 2 - \vec 1, \vec 3 - \vec 1, \cdots, \vec n - \vec 1$, y en consecuencia, orden $n-1$.
La descomposición de la representación definición de ${\mathbb{S}}_3$ obtenida en el Ejercicio 2.3 es, de hecho, la mejor que se puede obtener. Las dos subrepresentaciones que aparecen son irreducibles. En el Ejercicio 2.8 veremos que la representación estándar es irreducible. Por otra parte, al ser unidimensional, es obvio que la representación trivial es irreducible.
Si una representación $X$ de $G$ tiene un subespacio no trivial, entonces su complemento ortogonal con respecto a este producto escalar invariante también es invariante y no trivial. La restricción de $X$ a estos dos subespacios nos produce una descomposición más fina. Iterando este proceso, podemos escribir cualquier representación de $G$ como suma directa de representaciones irreducibles.
Un resultado de Maschke nos asegura que cualquier representación compleja de un grupo finito puede escribirse como la suma directa de representaciones irreducibles. Esto se demuestra utilizando que para cualquier espacio vectorial complejo sobre el que actúa un grupo finito $G$, podemos construir un producto escalar invariante bajo esta acción a través del operador de Reynolds: \[ \langle u,v \rangle = \frac{1}{|G|} \sum_{g \in G} \langle g \cdot u , g \cdot v \rangle. \] Por otra parte, si trabajamos con grupos infinitos este resultado no es necesariamente cierto. Un grupo que posee la propiedad de que todas sus representaciones pueden ser escritas como la suma directa de sus representaciones irreducibles se denomina semi-simple.
Queremos estudiar la estructura algebraica que poseen las representaciones de un grupo finito. Empezamos por definir un producto interno sobre el espacio de caracteres. Haremos un breve recuento de algunos hechos de naturaleza general para motivar la definición de un producto escalar en el espacio de carácteres. Primero observese que del isomorfismo natural entre $Hom(V,W) \cong V^* \otimes W$ deducimos que \[ Hom_G(V, W) = Hom(V,W)^G \cong (V^* \otimes W)^G \] donde $G$ actua sobre $\phi \in Hom(V, W)$ como $g(\phi)=g \circ \phi \circ g^{-1}$. (Para entender esta definición basta dibujar el diagrama conmutativo correspondiente.)
Ahora, dada cualquiera proyección $\pi$ de $G$-módulo $U$ sobre su espacio de invariantes $U^G$, la dimensión de $U^G$ viene dada por \[ tr \, \pi = \frac{1}{|G|} \sum tr(g). \] En el caso particular que nos concierne, la proyección de $V^* \otimes W$ sobre $(V^* \otimes W)^G$, tenemos que \[ tr \, \pi = \frac{1}{|G|} \sum_g \chi_{V^*}(g) \chi_W(g) = \frac{1}{|G|} \sum_g \chi_V(g^-1) \chi_W(g) \] ya que si es fácil ver que su $V$ y $W$ son representaciones, entonces $\chi_{V\otimes W}=\chi_V \chi_W$. Más aún, en general $\chi_{V^*}=\overline{\chi_V}$ y por ser $G$ un grupo finito todos los autovalores son raíces de la unidad y $\bar\chi_V= \chi_V(g^{-1})$.
Concluimos que \[ \dim(Hom_G(V_{},W_{})) = \frac{1}{|G|} \sum_{g \in G} \chi_V(g) \chi_W(g^{-1}). \]
Los enteros no negativos $m_i$ que aparecen en la ecuacion (\ref{mult-eq}) se denominan multiplicidades. En esta situación decimos que la representación irreducible $X^{(i)}$ aparece con multiplicidad $m_i$ en la representación $X$.
Los dos ejemplos canónicos de grupos semi-simples son los grupos finitos, y el segundo protagonista de nuestras lecciones: el grupo lineal general.
Sea $H$ un subgrupo de $G$. Queremos obtener una representación de $H$ a partir de una representación de $G$ (y viceversa). En la primera situación, el procedimiento es trivial. Si $X$ es una representación matricial de $G$ con carácter $\chi$, definimos la restricción de $X$ a $H$, que denotamos por $X\downarrow^G_H$, como $X\downarrow^G_H (h)=X(h)$, para cada $h \in H$. Al carácter de la representación resultante lo denotamos por $\chi\downarrow^G_H$. Es importante mencionar que, incluso si $X$ es una representación irreducible $X\downarrow^G_H$, en general, no lo es.
Construir una representación del grupo $G$ a partir de una representación del subgrupo $H$ es más sutil. Veamos primero que sucede en el caso de un grupo finito $G$. Consideremos una transversal $t_1, \ldots, t_k$ de $H$ en $G$; esto es, una colección de elementos de $G$ tales que el grupo $G$ es la unión disjunta de las clases $t_iH$. (Si $G$ es finito $k=|G|/|H|$ también lo es.)
Sea $Y$ una representación matricial de $H$ sobre el espacio vectorial $V$. Para cada $t_i$, consideramos una copia $t_iV$ de $V$, a cuyos elementos llamamos $t_iv$, con $v \in V$. Entonces, el grupo $G$ actúa de manera natural sobre $\oplus_i \, ( t_i Y )$; para determinar $g(t_iv)$ (donde $g\in G$, $i\in [k]$, $t_iv \in t_iV$) hacemos los siguiente: tenemos que $gt_i \in t_lH$ para un único valor de $l$; sea $gt_i=t_lh$. Entonces, para cada $t_iv\in t_iV$, definimos \[ g \cdot (t_iv) = t_l (h\cdot v) \in t_lV. \] Se puede demostrar que la representación que resulta no depende de la transversal utilizada para su construcción. Si calculamos la matriz correspondiente, obtenemos la siguiente definición de la inducción de $H$ a $G$:
El ejemplo anterior nos ilustra que, a pesar de que la representación trivial es irreducible, $1\uparrow_H^G$ no lo es en general.
Existe una elegante relación entre los procedimientos de inducción y restricción de representaciones.
Hasta ahora, siempre hemos trabajados con un espacio vectorial $V$, junto con una de sus bases. Esto nos ha permitido, por ejemplo, asociarle a cada homomorfismo una matriz. Pero, como sucede con frecuencia, es más fácil y elegante trabajar con espacios vectoriales sin la necesidad de fijar una base de antemano. Para esto introducimos la noción de $G$-módulo.
Sea $G$ un grupo (no necesariamente finito) y sea $V$ un espacio vectorial. Decimos que $V$ es un $G$-módulo si existe un homomorfismo de grupos $\rho : G \to GL(V)$ de $G$ al grupo $GL(V)$ de las transformaciones lineales invertibles del espacio vectorial $V$. Nótese que al fijar una base para $V$, cada uno de estos homomorfismos $\rho$ nos define una representación matricial de $G$. Similarmente, cada representación matricial de $G$ nos produce un tal $\rho$. Las nociones de $G$-módulo y de representación matricial de $G$ son equivalentes desde este punto de vista. Hablaremos de una representación cuando no queremos enfatizar si estamos trabajando con (o sin) una base.
Sean $V$ y $W$ dos $G$-módulos. Un $G$-homomorfismo es una transformación lineal $\theta : V \rightarrow W$ tal que $\theta ( \pi v) = \pi \theta (v)$ para cada $\pi \in G$. Si $\theta$ es invertible, decimos entonces que es un $G$-isomorfismo. A lo largo de estas lecciones asumimos que todos los $G$-módulos con los que trabajaremos son de dimensión finita.
Denotamos por ${\mathbb{C}}[G]$ el álgebra del grupo $G$, es decir, el álgebra definida por las combinaciones lineales de elementos de $G$, donde la multiplicación viene dada por el producto de $G$. Obsérvese que ${\mathbb{C}}[G]$ tiene naturalmente estructura de $H$-módulo, lo que nos permite tomar el siguiente producto tensorial de ${\mathbb{C}}[H]$-módulos.
La inducción de representaciones se puede definir de manera concisa en el lenguaje de $G$-módulos. Sea $H$ un subgrupo de $G$, y sea $V$ un $H$-módulo, definimos \[ Ind_H^G \, V = \mathbb{C}[G] \otimes_{\mathbb{C}[H]}V \] Nótese que $\mathbb{C}[G]$ tiene una estructura natural de $\mathbb{C}[G]$-módulo (dada por la restricción), y que estamos tomando el producto tensorial de $\mathbb{C}[H]$-módulos.
Hemos obtenido entonces una representación de $G$ a partir de la representación $V$ de $H$ ya que $Ind_H^G \, V$ tiene estructura de $G$-módulo. Dejamos los detalles de verificar que ambas definiciones coinciden al lector familiarizado con la teoría de módulos.
Sea $V$ un espacio vectorial complejo de dimensión $m$. Una representación de $GL(E)$ se dice polinomial si la aplicación \[ X : GL(V) \to GL(W) \] viene descrita por polinomios. Esto es, si después de escoger bases para $V$ y $W$ las $N^2$ funciones coordinadas son polinomios en las $m^2$ variables determinadas por las entradas de una matriz genérica en $GL(V)$. Similarmente, decimos que la representación es racional u holomórfica cuando estas funciones lo son.
En este pequeño apartado procedemos a dar una construcción que nos permite asociar a cualquier representación del grupo simétrico una representación polinomial del grupo lineal general. Los detalles se encuentran en el libro de William Fulton [5]W. Fulton, Young tableaux. With applications to representation theory and geometry. London Mathematical Society Student Texts, 35. Cambridge University Press, Cambridge, 1997.. Recordemos que estamos trabajando sobre un espacio vectorial $V$, de dimensión $m$. El grupo simétrico ${\mathbb{S}}_n$ actúa sobre $V^{\otimes n}$ por la derecha (es decir, permuta las posiciones) \begin{align*} &V^{\otimes n} = V \otimes_{{\mathbb{C}}} V \otimes_{{\mathbb{C}}} \cdots \otimes_{{\mathbb{C}}} V,\\ &(u_1 \otimes u_2 \otimes \cdots \otimes u_n) \cdot \sigma = u_{\sigma(1)} \otimes u_{\sigma(2)} \otimes \cdots \otimes u_{\sigma(n)}. \end{align*} para cada $u_i \in V$ y $\sigma \in {\mathbb{S}}_n$. Esta acción le proporciona a $V^{\otimes n}$ la estructura de ${\mathbb{S}}_n$-módulo. Por otra parte, a cada representación $M$ de ${\mathbb{S}}_n$ le asociamos el espacio vectorial \[ \mathbb{V}(M) = V^{\otimes n} \otimes_{{\mathbb{C}}[{\mathbb{S}}_n]} M. \] En consecuencia, tenemos que en $\mathbb{V}(M)$, para cada $w \in V^{\otimes n} $, $v \in M$ y $\sigma \in {\mathbb{S}}_n$ \[ (w \cdot \sigma) \otimes v = w \otimes (\sigma \cdot v). \]
Como el grupo lineal general $GL(V)$ actúa a la izquierda en $V$, y como esta acción se puede extender diagonalmente a $V^{\otimes n}$ de la siguiente manera \[ g \cdot ( u_1 \otimes u_2 \otimes \cdots \otimes u_n ) = g \cdot u_1 \otimes g \cdot u_2 \otimes \cdots \otimes g \cdot u_n, \] $V^{\otimes n}$ también tiene la estructura de $GL(V)$-módulo. Es inmediato ver que ambas acciones conmutan, de manera que $GL(V)$ también actúa sobre $\mathbb{V}(M)$ : $g \cdot (w \otimes v) = (g \cdot w) \otimes v$.
Concluimos entonces que tanto $\mathbb{V}(M)$ como $V^{\otimes n}$ tienen la estructura de $(GL(E),{\mathbb{S}}_n)$-módulo.
Veamos algunos ejemplos de esta construcción. Si $M$ es la representación trivial de ${\mathbb{S}}_n$, entonces $\mathbb{V}(M)$ corresponde a las potencias simétricas de $V$: $\mathbb{V}(M)=Sym^n(V).$ Similarmente, si $M$ es la representación alternante de ${\mathbb{S}}_n$, obtenemos entonces las potencias simétricas de $V$, $\mathbb{V}(M)=\bigwedge^n V$. Finalmente, si $M={\mathbb{C}}[{\mathbb{S}}_n]$ es la representación regular de ${\mathbb{S}}_n$, entonces $\mathbb{V}(M)=V^{\otimes n}$.
Esta construcción es functorial: dado cualquier homomorfismo $\phi : M \to N$ de ${\mathbb{S}}_n$-módulos, obtenemos un homomorfismo $\mathbb{V}(\phi)= \mathbb{V}(M) \to \mathbb{V}(N)$ de $GL(V)$-módulos. Una descomposición en suma directa $M=\oplus M_i$ de ${\mathbb{S}}_n$-módulos determina una descomposición de $GL(V)$-módulos $\mathbb{V}(M) = \oplus \mathbb{V}(M_i)$.
El teorema de Maschke nos dice que cualquier representación compleja del grupo simétrico puede ser descompuesta como suma directa de representaciones irreducibles. Equivalentemente, cualquier ${\mathbb{S}}_n$-módulo se puede escribir como suma de ${\mathbb{S}}_n$-módulos irreducibles. Las representaciones irreducibles de $\mathbb{S}_n$ (${\mathbb{S}}_n$-módulos irreducibles) corresponden a las clases de conjugación del grupo simétrico $\mathbb{S}_n$, que a su vez, como vimos en el ejercicio 1.2, vienen indexadas por las particiones de $n$.
En esta sección veremos como varios objetos combinatorios (tableau de Young, tableau semiestándar, etc) aparecen de manera natural en el estudio de estas representaciones. Presentamos una elegante construcción de un conjunto completo de representaciones irreducibles del grupo simétrico basada en las notas de François Bergeron [4]François Bergeron, Combinatoire algebrique, LaCIM, Universite de Quebec á Montreal. versión de 8 avril, 2001.. A partir de este conjunto de representaciones irreducibles complejas del grupo simétrico construiremos una familia completa de representaciones polinomiales complejas irreducibles del grupo lineal general ilustrando la dualidad que existe entre ambas teorías.
Comenzamos por definir una importante familia $\{{\mathcal{H}}^{\lambda}\}$ de representaciones por permutaciones de ${\mathbb{S}}_n$, indexadas por particiones de $n$. En general, las representaciones $H^{\lambda}$ no son irreducibles. Sin embargo, tienen la siguiente propiedad : Al descomponer a $\mathcal{H}^\mu$ como suma de representaciones irreducibles, la representación $S^{\mu}$ aparece con multiplicidad uno, y sólo aquellas representaciones irreducibles $S^{\lambda}$ indexadas por particiones $\lambda \unrhd \mu$, en el orden de dominanción, aparecen con multiplicidad mayor o igual a uno.
Posteriormente, construiremos un conjunto de representaciones irreducibles del grupo simétrico. Concluimos esta sección con la descripción de la descomposición de las representaciones $\{{\mathcal{H}}^{\lambda}\}$ como suma directa de representaciones irreducibles.
Sean $k$ y $n$ dos números dados tales que $k \ge n$. Un tableau inyectivo $t$ de forma $\lambda \vdash n$ es una función inyectiva $t$ del conjunto de casillas del diagrama de $\lambda$ al conjunto $ [k]$, que denotamos por $t : \lambda \to [k]$. Equivalentemente, es una manera de asociar a cada casilla del diagrama de $\lambda$ un número entre $1, 2, \cdots, k$, sin repetición.
Sea $l$ una casilla del diagrama de $\lambda$, $t(l)$ la entrada correspondiente a $\lambda$ y $f(l)$ la fila a la que pertenece $l$. Definimos el peso de un tableau inyectivo $\lambda$ como \[ x^t=\prod_{l \in \lambda} x_{t(l)}^{f(l)-1}. \] Es importante no confundir esta noción con la definición de peso de un tableau dada en la introducción.
El grupo simétrico ${\mathbb{S}}_k$ actúa sobre cualquier tableaux $t : \lambda \to [k]$ de la manera canónica: \begin{align*} \sigma \cdot t &: \lambda \to [k] \\ \sigma \cdot t(c) &= \sigma(t(c)). \end{align*}
El estabilizador de esta acción sobre $T$ es un subgrupo de Young, $ {\mathbb{S}}_{F_1} \times {\mathbb{S}}_{F_2} \times \cdots {\mathbb{S}}_{F_{\ell}},$ donde ${\mathbb{S}}_{F_i}$ es el grupo de permutaciones de las entradas de la $i$-ésima fila de $T$.
Por ejemplo, ${\mathcal{H}}^{ (2,1) }= {\mathcal L}[ x_3, x_2, x_1] $ ya que
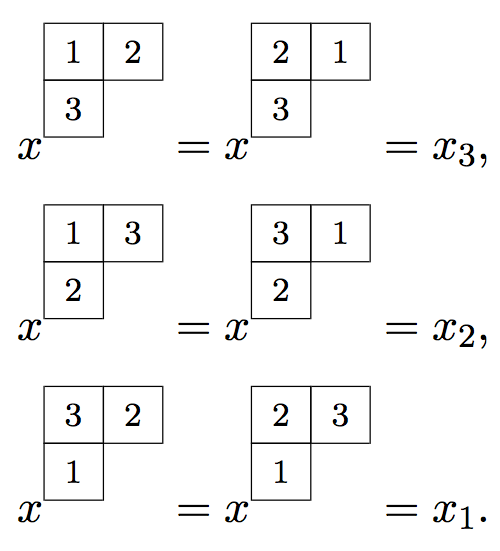
Como vemos en este ejemplo, en general varios tableaux inyectivos tienen el mismo peso. Para evitar esta redundancia, añadimos la condición adicional de que las entradas en cada fila se encuentren ordenadas en orden creciente.
La noción de tableau inyectivo también nos permite construir una familia completa de representaciones irreducibles de ${\mathbb{S}}_n$.
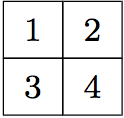 , entonces su estabilizador es $\mathbb{S}_{\{1,3\}}\times\mathbb{S}_{\{2,4\}}$, y
$
a_t=(x_3-x_1)(x_4-x_2).
$
Calcular el polinomio que corresponde al otro tableau estándar de tipo $(2,2)$.
, entonces su estabilizador es $\mathbb{S}_{\{1,3\}}\times\mathbb{S}_{\{2,4\}}$, y
$
a_t=(x_3-x_1)(x_4-x_2).
$
Calcular el polinomio que corresponde al otro tableau estándar de tipo $(2,2)$.
Sea $S$ un conjunto con cardinalidad $k$. En lo que sigue, denotamos por $\Delta_k(S)$ el determinante de Vandermonde asociado a las variables en $S$. Veamos como podemos utilizar estas funciones para dar una descripción alternativa del conjunto completo de representaciones irreducibles de $\mathbb{S}_n$.
En general, se conoce muy poco acerca de cómo descomponer una representación como suma directa de sus representaciones irreducibles. El caso particular de las representaciones de ${\mathcal{H}}^{\lambda}$ es especial. Su descomposición se describe simplemente en el lenguage de la combinatoria de los tableros de Young y viene descrita por la regla de Young.
Sabemos que el coeficiente de Kostka $K_{\lambda,1^n}= f^{\lambda}$, es igual al número de tableaux estándar de forma $\lambda$. Tenemos entonces que \[ {\mathcal{H}}^{(1^n)} = \oplus_{\lambda \vdash n} ( S^{{\lambda}})^{\oplus f^{\lambda}} \]
En la sección anterior vimos como obtener las potencias simétricas y alternantes a partir de las representaciones trivial y alternante del grupo simétrico. Veamos qué sucede al aplicar el functor $\mathbb{V}(\cdot)$ a las representaciones del grupo simétrico que acabamos de construir.
Como un ejercicio, el lector deberá verificar que dada cualquier partición $\lambda=(\lambda_1, \lambda_2, \cdots, \lambda_l)$, obtenemos la siguiente representación de $GL(V)$: \[ \mathbb{V}(\mathcal{H}^\lambda)\cong Sym^{\lambda_1}(V)\otimes Sym^{\lambda_2}(V)\otimes \cdots \otimes Sym^{\lambda_l}(V). \] Al igual que en el caso del grupo simétrico, esta representación no es irreducible, y su descomposición en irreducibles viene dada por los coeficientes de Kostka.
A partir de las representaciones irreducibles de los grupos simétricos ${\mathbb{S}}_n$, obtenemos a un conjunto completo de representaciones irreducibles de $GL(V)$.
La familia de representaciones polinomiales del grupo lineal general $GL(V)$ \[ V^{\lambda}:= \mathbb{V}(S^{\lambda}) \] donde $\lambda$ es una partición de longitud $\le \dim(V)$, es una familia completa de representaciones polinomiales irreducibles de $GL(V)$. Nótese que, al no tener ninguna condición sobre $|\lambda|$ esta es una familia infinita.
Más aún, tenemos la siguiente descomposición de $V^{\otimes n}$ como $GL(V)$-módulo : \[ V^{\otimes n} = \mathbb{V}({\mathbb{C}}[{\mathbb{S}}_n]) \cong \bigoplus_{\lambda \vdash n} (V^{\lambda})^{\oplus f^{\lambda}} \] donde la suma se toma sobre todas las particiones de $n$ de longitud menor o igual a $dim(V)$.
El algoritmo de Robinson-Schensted-Knuth (RSK), ver [8]Richard P. Stanley, Enumerative combinatorics. Vol. 2. With a foreword by Gian-Carlo Rota and appendix 1 by Sergey Fomin. Cambridge Studies in Advanced Mathematics, 62. Cambridge University Press, Cambridge, 1999., nos proporciona una biyección entre el número de funciones $[n] \to [m]$, y las parejas de tableaux, el primero estándard con entradas en $n$, el segundo semi-estándar con entradas en $m$. En este contexto nos proporciona una demostración combinatoria de esta identidad, al nivel de espacios vectoriales.
Ya en nuestra primera lección, introdujimos las funciones simétricas a través del estudio de las matrices no negativas. En esta segunda lección las estudiaremos desde un punto de vista algebraico. Para esto haremos un énfasis particular en la relación que existe entre la estructura de álgebra de Hopf de funciones simétricas y la teoría de representaciones del grupo simétrico y del grupo lineal general.
A un conjunto ordenado de variables lo llamamos alfabeto. Resulta muy útil escribir un alfabeto como una suma formal de variables. Por ejemplo, el alfabeto $X= \{x_1, x_2, \ldots \}$ lo escribimos como $ X=x_1+x_2+\cdots $. Denotamos por $\mathbb{Z}[|X|]$ al álgebra de las series formales en el alfabeto $X$. Si $\pi$ es una permutación en $\mathbb{S}_n$ y $f \in \mathbb{Z}[|X|]$ definimos \[ f[X] \cdot\pi =p(x_1, x_2, \cdots, x_n, x_{n+1} \cdots) = f(x_{\pi(1)}, x_{\pi(2)}, \cdots, x_{\pi{(n)}}, x_{n+1} \cdots) \]
Denotamos por $Sym$ la subálgebra de ${\mathbb{Z}}[|X|]$ formada por las series, con un número finito de componentes no nulas, que son invariantes bajo esta acción (para cada $n \in \mathbb{N}$). Por ejemplo, \begin{align*} p_k=x^k_1+x^k_2+x^k_3+\ldots &\in Sym\\ 1+p_k+p_k^2+\ldots = \frac{1}{1-p_k} &\notin {Sym} \end{align*} El segundo es un ejemplo de una función que, a pesar de ser invariante, tiene un número infinito de componentes no nulas. Tales funciones pertenecen a la completación de ${Sym}$. Denotamos por ${Sym}^{(k)}$a la componente homogénea de grado $k$ de ${Sym}$.
Sea $\lambda=(\lambda_1, \lambda_2, \cdots, \lambda_{\ell})$ una partición. Definimos tres familias de funciones simétricas, las llamadas bases multiplicativas, \begin{align*} &&e_{\lambda}=e_{\lambda_1} e_{\lambda_2} \cdots e_{\lambda_{\ell}}, &&p_{\lambda}=p_{\lambda_1} p_{\lambda_2} \cdots p_{\lambda_{\ell}}, &&h_{\lambda}=h_{\lambda_1} h_{\lambda_2} \cdots h_{\lambda_{\ell}}. \end{align*} donde $h_n$ es igual a la suma de todos los monomios de grado $n$, $e_m$ la suma de todos los monomios de grado $n$ libres de cuadrados, y $p_n$ la suma de las potencias $n$-ésimas de los elementos de $X$. Por ejemplo, si $X=x+y+z$, entonces $h_2[X]=x^2+y^2+z^2+xy+xz+yz$, $e_2[X]=xy+xz+yz$ y $p_2[X]=x^2+y^2+z^2$.
Este teorema no es difícil de demostrar. Se puede hacer estudiando la matriz de cambio de bases entre las funciones simétricas elementales y las monomiales, y observando que son triangulares y con todas sus entradas en la diagonal principal iguales a uno. O se puede hacer utilizando al orden lexicográfico en el algoritmo de la división de Buchberger.
En el siguiente ejercicio estudiaremos las matrices de cambio de base entre las bases multiplicativas de ${Sym}$. Obtendremos entonces que las tres familias multiplicativas que hemos introducidos son, como su nombre lo sugiere, bases para $Sym$.
Esto nos permite definir ${Sym}$ como el álgebra de polinomios $\mathbb{Z}[e_1, e_2, \cdots]$, donde las $e_i$ son variables formales, y luego introducir las otras bases de ${Sym}$ utilizando las identidades que acabamos de encontrar.
Ya en la primera de nuestra serie de lecciones introdujimos la más intrigante de las bases para el álgebra de las funciones simétricas; la base de Schur. En aquel momento las funciones de Schur se definieron utilizando la matriz de Jacobi—Trudi que las expresa en la base de las funciones completas homogéneas. Daremos ahora la definición combinatoria para esta importante base.
Sea $X=x_1+x_2+\ldots$ un alfabeto y sea $\lambda$ una partición de $n$.
La función de Schur $s_{\lambda}$ se define como \[ s_{\lambda}[X]=\sum_{T}x^T \] donde sumamos sobre todos los tableaux semi-estándar $T$ de forma $\lambda$ y donde $x^T$ denota el peso del tableau $T$.
Definimos las funciones de Schur sesgadas $s_{\lambda/\mu}[X]$ similarmente, pero ahora sumamos sobre todos los tableaux semi-estándar sesgados $T$ de forma $\lambda / \mu$.
Por ejemplo, \begin{align*} s_{(2,1)}= m_{(2,1)}+2 m_{(1,1,1)}.\\ s_{(2,1)/(1)}=h_1^2. \end{align*} No es evidente de esta definición que las funciones de Schur sean simétricas. Esto se puede ver directamente utilizando un elegante argumento de D. Knuth (ver [6]Bruce E. Sagan, The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Second edition. Graduate Texts in Mathematics, 203. Springer-Verlag, New York, 2001.).
De la definición combinatoria de las funciones de Schur se puede conseguir su desarrollo en la base de las funciones simétricas monomiales. Recuerde que el coeficiente de Kostka $K_{\lambda, \mu}$ se define como el número de tableaux semi-estándar de forma $\lambda$ y contenido $\mu$. El hecho de que las funciones de Schur sean simétricas es equivalente a la igualdad $K_{\lambda,\mu}=K_{\lambda,\tilde\mu}$ para cualquier rearreglo de las parte de $\mu$. Concluimos que \[ s_{\lambda} = \sum_{\mu} K_{\lambda, \mu} m_{\mu}. \]
Definimos un producto escalar sobre ${Sym}$, que denotamos por $\langle \,\,, \, \rangle$, diciendo que la base de Schur es una base ortonormal: \[ \langle s_{\mu}, s_{\nu} \rangle = \delta_{\mu,\nu}. \] donde $\delta_{\mu,\nu}$ es la función delta de Kronecker. De la ortonormalidad de la base de Schur vemos que la involución $\omega$ es una isometría.
Este mismo producto escalar se puede definir de manera equivalente diciendo que $\langle m_{\lambda}, h_{\mu} \rangle=\delta_{\lambda,\mu},$ o que $\langle p_{\lambda}, p_{\mu} \rangle=\delta_{\lambda,\mu}z_{\lambda}.$
El producto de dos funciones simétricas es una función simétrica, de manera que ${Sym}$ tiene una estructura de álgebra.
Los coeficientes de Littlewood-Richardson juegan un rol fundamental en la teoría de las funciones simétricas (y sus aplicaciones a la teoría de representaciones, entre muchas otras áreas). La famosa regla de Littlewood-Richardson nos proporciona una interpretación combinatoria para estos coeficientes (cuentan la cardinalidad de un cierto conjunto de tableaux semi-estándar definido en función de $\lambda, \mu$ y $\nu$.) Esta interpretación combinatoria también nos proporciona una algoritmo (ineficiente) para calcularlos.
Veamos ahora otra instancia en la que los coeficientes de Littlewood-Richardson aparecen de manera natural en la teoría de las funciones simétricas.
Las funciones de Schur sesgadas se expresan en la base de Schur utilizando los coeficientes de Littlewood-Richardon. \[ s_{\lambda \setminus \mu} =\sum_{\nu} c^{\lambda}_{\mu,\nu} s_{\nu} \] Por lo tanto, las funciones de Schur sesgadas son el adjunto de la multiplicación por una función de Schur. Más precisamente, definimos una operación lineal $s_{\mu}^{\perp}$ sobre $Sym$, declarando $s_{\mu}^{\perp} s_{\lambda}=s_{\lambda/ \mu}$. (Observe que por definición $s_{\mu}^{\perp} s_{\lambda}=0$ si $\mu$ no se encuentra contenido en $ \lambda$.)
La identidad $ c_{\mu,\nu}^{\lambda} = \langle s_{\lambda}, s_{\mu}s_{\nu} \rangle = \langle s_{\lambda / \mu}, s_{\nu} \rangle $ implica que $s_{\mu}^{\perp}$ es el adjunto de la multiplicación por $s_\mu$; es decir, que para cualquier par de funciones simétricas $f$ y $g$ : \[ \langle s_{\mu} \, f, g \rangle = \langle f, s_{\mu}^{\perp} g \rangle. \]
Las funciones simétricas, junto con la operación de multiplicación, forman un álgebra graduada, pero tienen una estructura mucho más rica. Antes de empezar a describirla introduciremos las nociones de coálgebra, biálgebra y álgebra de Hopf.
Recuerdese que denotamos por $f[X]$ a la función $f$ evaluada en el alfabeto $X$. Explícitamente, \[ f[X]= f(x_1, x_2, \ldots) \] Ahora queremos pasar a considerar una función simétrica como un alfabeto. Por ejemplo, a la función simétrica $ p_2 = x_1^2 + x_2^2 + x_3^2+ \cdots $ la identicamos con el conjunto de ``variables'' $\{ x_1^2, x_2^2, x_3^2, \cdots \}$.
Definimos el pletismo (o sustitución) de funciones simétricas trabajando con la base de las series de potencia. Como nos sugiere el ejemplo anterior, queremos que $p_n[p_2]=p_{2n}$. Para esto, procedemos de la siguiente manera: Sea $g$ una serie de potencias formal sobre el anillo de las series formales ${\mathbb{Q}}[[x_1, x_2, \cdots]]$. Escribimos \[ g=\sum_{\alpha} u_{\alpha} \] donde cada $u_{\alpha}$ es un monomio (con coeficiente uno) en ${\mathbb{Q}}[[x_1, x_2, \cdots]]$. Por ejemplo, $2x=x+x$.
Definimos \begin{align*} p_n[g] &= \sum_{\alpha} c_{\alpha} u_{\alpha}^n\\ p_{\lambda}[g]&= p_{\lambda_1}[g] p_{\lambda_2}[g] \cdots p_{\lambda_n}[g] \end{align*} donde $\lambda=(\lambda_1, \lambda_2, \cdots, \lambda_n)$.
Por ejemplo, utilizando la definición de pletismo, vemos que \[ p_n[2x+2y]=p_n[x+x+y+y]=x^n+x^n+y^n+y^n=2x^n+2y^n. \]
Finalmente, definimos $f[g]$, para cualquier función simétrica $f$, diciendo que $f[g]$ es lineal en $f$. Para calcularlo empezamos por expresar a $f$ en la base de las series de potencias.
El pletismo no es una transformación lineal, por ejemplo $p_{\lambda}[2 x] =2^{\ell(\lambda)}p_{\lambda}[x].$
Para evaluar $s_{\lambda}[X+Y]$ podemos asumir que todas las variables $x_i \in X$ son menores que todas las $y_j \in Y$, esto es posible ya que $s_{\lambda}$ es una función simétrica. De la definición combinatoria de una función de Schur sesgada obtenemos que $s_{\lambda}[X+Y]$ es una suma de funciones simétricas de la forma $s_\mu[X]s_{\lambda / \mu}[Y]$, donde $\mu \in \lambda$ es la partición que definen las entradas en $X$ y $\lambda / \mu$ es la partición que definen las entradas en $Y$.
\begin{align*} s_{\lambda}[X+Y]&=\sum_{\mu\in \lambda} s_{\mu}[X] s_{\lambda/ \mu}[Y]=\sum_{\mu, \nu} c_{\mu, \nu}^{\lambda} \, s_{\mu}[X] s_{\nu}[Y] \end{align*}
Un problema abierto importante en la combinatoria algebraica es el de entender el desarrollo de la función $s_{\lambda}[XY]$ en la base de Schur. Por otra parte, el desarrollo de $s_{(n)}[XY]=h_n[XY]$ es particularmente útil y viene dada por el kernel de Cauchy, que nos proporciona el desarrollo de $h_n[XY]$ en cualquier par de bases duales\footnote{Las bases $u_{\lambda}$ y $v_{\lambda}$ son duales si $\langle u_{\lambda}, v_{\nu}\rangle=\delta_{\lambda,\nu}$} $u_{\lambda}$ y $v_{\lambda}$ :
Pasamos ahora a describir la estructura de álgebra de Hopf de $Sym$ con respecto a la multiplicación ordinaria de series de potencias. Identificamos ${Sym} \otimes {Sym}$ con las funciones en dos alfabetos $X$ y $Y$ que son simétricas en cada alfabeto separadamente. Bajo esta identificación $f\otimes g$ corresponde al producto $f[X]g[Y]$.
Utilizando la operación de suma de alfabetos, definimos una operación de comultiplicación sobre ${Sym}$, \begin{align*} \Delta : {Sym} &\to {Sym} \otimes {Sym}\\ \Delta f &= f[X+Y] \end{align*} Se tiene que $({Sym}, \Delta)$ tiene estructura de coálgebra. La counidad $\epsilon$ viene dada por la proyección $ \epsilon : f \mapsto f(0,0,\ldots)$.
El antípoda en esta biálgebra graduada viene dada por una pequeña variante de la involución $\omega$. En efecto, La involución \begin{align*} \bar \omega : {Sym} \to {Sym}\\ \bar \omega (h_i) = (-1)^i e_i \end{align*} para cada $i \ge 1$, es una antípoda para ${Sym}$. Concluimos entonces que
La familia $({Sym}, \mu, 1, \Delta, \epsilon, \bar \omega)$ es un álgebra de Hopf graduada, donde $\mu$ es la multiplicación heredada del anillo de las series formales, $1$ es su identidad, el coproducto viene dado por $\Delta f= f[X+Y]$, y su counidad por $ \epsilon(f)=f(0,0,\ldots)$.
Más aún, el producto escalar de ${Sym}$ es compatible con la estructura de biálgebra en el sentido de que \begin{align*} \langle \Delta f, g \otimes h \rangle &= \langle f, gh \rangle\\ \langle \bar \omega f, \bar \omega g \rangle &= \langle f, g \rangle\\ \langle f, 1 \rangle&= \epsilon(f) \end{align*}
Ahora pasamos a estudiar una segunda estructura de biálgebra para $Sym$ (aunque no de álgebra de Hopf). Para esto introducimos el producto de Kronecker que, como veremos, corresponde al producto tensorial interno entre representaciones del grupo simétrico, a través de la operación del producto de dos alfabetos.
El producto de alfabetos nos define una segunda comultiplicación sobre ${Sym}$: \begin{align*} \Delta^{\star} : {Sym} &\to {Sym} \otimes {Sym}\\ \Delta^{\star} f &= f[XY]. \end{align*} cuya counidad viene dada por \[ \epsilon^{\star} f = f(1,0,0,\ldots) \] para toda $f \in {Sym}.$
Los coeficientes de Kronecker nos permiten definir el producto de Kronecker entre $s_{\mu}$ y $s_{\nu}$ utilizando para esto a la base de Schur : \begin{equation}\label{defkron} s_{\mu} \star s_{\nu} = \sum_{\lambda } {\gamma^{\lambda}_{\mu,\nu}} s_{\lambda} \end{equation} Extendiendo a ${Sym}$ por linealidad, obtenemos una segunda operación de multiplicación para $Sym$. Llamamos a esta operación producto de Kronecker (o producto interno).
El siguiente ejercicio muestra que la unidad con respecto al producto de Kronecker está dada por una suma infinita de funciones homogéneas completas, y por lo tanto no está en $Sym$ sino en su completación.
En esta sección revisitaremos la teoría de representaciones del grupo simétrico. En la sección 3 ya construimos una familia completa de representaciones irreducibles de ${\mathbb{S}}_n$, para cada $n$. Ahora queremos estudiar simultáneamente estas familias de representaciones irreducibles desde un punto de vista algebraico.
Sea ${R({\mathbb{S}}_n)}$ el grupo de Grothendieck del grupo simétrico ${\mathbb{S}}_n$. Esto es, el grupo abeliano generado por las clases de equivalencia de las representaciones irreducibles del grupo simétrico con la operación de suma directa. Definimos \[ {R({\mathbb{S}})} = \{ {R({\mathbb{S}}_n)} : n \ge 1 \} \] junto con la inclusión canónica: \[ \rho_{n,m} : {R({\mathbb{S}}_n)} \times R({\mathbb{S}}_m) \hookrightarrow R({\mathbb{S}}_{n+m}). \] que considera un par de permutaciones $(\pi,\sigma)$ en ${\mathbb{S}}_n\times{\mathbb{S}}_m$ como una permutación de ${\mathbb{S}}_{m+m}$ aplicando $\pi$ a los números $1, \cdots, n$ y $\sigma$ a $n+1, \cdots, m$ de la manera canónica : $\sigma(n+i):=\sigma(i)$.
Sobre ${R({\mathbb{S}})}$ se puede definir una estructura de álgebra de Hopf y una segunda estructura de biálgebra que, como veremos, corresponden a las estructuras que acabamos de estudiar sobre ${Sym}$.
Sean $X$ e $Y$ dos ${\mathbb{S}}_n$-módulos. Definimos el producto entre $X$ e $Y$, que denotamos por $X \circ Y$, a través del procedimiento de inducción de representaciones: \begin{align}\label{producto} X \circ Y := \rho_{n,m} (X \otimes Y) \big\uparrow_{{\mathbb{S}}_n \times {\mathbb{S}}_m}^{{\mathbb{S}}_{n+m}} \end{align}
La unidad de esta álgebra de Hopf viene dada por la unidad del álgebra $R({\mathbb{S}})$; es decir, la representación trivial de ${\mathbb{S}}_0$.
El coproducto viene dado por la suma de las restricciones de $R({\mathbb{S}}_n) $ a $R({\mathbb{S}}_i) \otimes R({\mathbb{S}}_j)$, para $i+j=n$ enteros no negativos. \begin{align*} \Delta : R({\mathbb{S}}_n) &\to \sum_{i+j=n} R({\mathbb{S}}_i) \otimes R({\mathbb{S}}_j)\\ \Delta(X) &= \sum_{i + j = n} X \big\downarrow^{{\mathbb{S}}_{i+j} }_{{\mathbb{S}}_i \times {\mathbb{S}}_j} \end{align*}
La counidad está definida por la proyección sobre $R({\mathbb{S}}_0)$ y nos da la multiplicidad de la representación trivial de ${\mathbb{S}}_0$.
Nótese que no es trivial que la comultiplicación sea un morfismo de álgebras. Esto es una consecuencia del teorema de Mackey. Para una exposición completa de estos resultados ver el libro de Zelevinski [9]Andrei V. Zelevinsky, Representations of finite classical groups. A Hopf algebra approach. Lecture Notes in Mathematics, 869. Springer-Verlag, Berlin-New York, 1981..
El antípoda corresponde (salvo por un signo) a tomar el producto tensorial con la representación alternante.
Sean $X$ e $Y$ dos ${\mathbb{S}}_n$-módulos. El producto de Kronecker (también llamado producto tensorial interno) se define como el ${\mathbb{S}}_n$-módulo $X \otimes Y$ junto con la acción diagonal del grupo simétrico. Esto es, para cada $\pi \in {\mathbb{S}}_n$ \[ \pi ( X \otimes Y) = \pi X \otimes \pi Y \] Denotamos el ${\mathbb{S}}_n$-módulo resultante por $X \star Y$. Nótese que si $\chi$ es el carácter de $X$ y $\phi$ el carácter de $Y$, entonces el carácter del producto de Kronecker viene dado por $(\chi\phi) (\pi) = \chi(\pi) \phi(\pi)$.
Los coeficientes de Kronecker también pueden ser definidos como las multiplicidades de las representaciones irreducibles en el producto tensorial de dos representaciones irreducibles del grupo simétrico. Luego veremos que esta definición es equivalente a la que dimos en la sección anterior en término de operaciones entre alfabetos.
Si $\mu$ y $\nu$ son particiones de $n$, se definen los coeficientes de Kronecker ${\gamma^{\lambda}_{\mu,\nu}}$ como \[ \chi^{\mu}\chi^{\nu}=\sum_{\lambda \vdash n} {\gamma^{\lambda}_{\mu,\nu}} \chi^{\lambda}. \]
Equivalentemente, la siguiente ecuación define los coeficientes de Kronecker y demuestra que son simétricos en $\mu, \nu $ y $\lambda$: \[ {\gamma^{\lambda}_{\mu,\nu}}=\langle \chi^{\lambda}, \chi^{\mu}\chi^{\nu} \rangle_{{\mathbb{S}}_n}= \frac{1}{n!} \sum_{\sigma \in {\mathbb{S}}_n} \chi^{\lambda}(\sigma) \chi^{\mu}(\sigma) \chi^{\nu}(\sigma), \] donde $\langle \,\,\, , \, \rangle_{{\mathbb{S}}_n}$ es el producto escalar en el espacio generado por los caracteres de ${\mathbb{S}}_n$, sus funciones de clase.\footnote{La barra de conjugación desaparece en este producto porque todas las representaciones irreducibles de ${\mathbb{S}}_n$ pueden ser construidas sobre $\mathbb{Q}$.}
Extendemos la definición del producto de Kronecker a $R({\mathbb{S}})$ diciendo que el producto de Kronecker entre una representación ${\mathbb{S}}_n$ y otra de ${\mathbb{S}}_m$ es cero si $n \ne m$.
Es importante darse cuenta que si $X$ es un ${\mathbb{S}}_n$-módulo y $Y$ es un ${\mathbb{S}}_m$-módulo, entonces $X \circ Y$ es un ${\mathbb{S}}_{m+n}$-módulo y $X * Y$ es un ${\mathbb{S}}_n$-módulo.
Ahora nos proponemos explicar la relación existente entre la teoría de representaciones del grupo simétrico y la funciones simétricas ${Sym}$. Las funciones simétricas juegan el rol de funciones generatrices para los caracteres de las representaciones del grupo simétrico.
Este resultado central nos describe elegantemente la relación que existe entre la teoría de las funciones simétricas, y la teoría de representaciones del grupo simétrico, [5]W. Fulton, Young tableaux. With applications to representation theory and geometry. London Mathematical Society Student Texts, 35. Cambridge University Press, Cambridge, 1997., [6]Bruce E. Sagan, The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Second edition. Graduate Texts in Mathematics, 203. Springer-Verlag, New York, 2001., [7]Richard P. Stanley, Enumerative combinatorics. Vol. 1. With a foreword by Gian-Carlo Rota. Corrected reprint of the 1986 original. Cambridge Studies in Advanced Mathematics, 49. Cambridge University Press, Cambridge, 1997.}. Es este resultado el que nos permite definir la aplicación característica de Frobenius.
Sea $CF^k$ el conjunto de todas las funciones de clase $f : {\mathbb{S}}_k \to \mathbb{Q}$ (funciones constantes en las clases de conjugación de ${\mathbb{S}}_k$.) En $CF^k$ existe un producto escalar natural definido por \[ \langle f, g\rangle = \frac{1}{n!} \sum_{\pi \in {\mathbb{S}}_k} f(\pi)g(\pi) \] Escribimos $\langle X, Y \rangle$ cuando $X$ y $Y$ son representaciones de ${\mathbb{S}}_k$ con carácteres $\phi$ y $\chi$, respectivamente.
Estamos interesados en estudiar la siguiente transformación lineal :
El teorema de Frobenius nos dice entonces que \[ {\bf ch}(\chi^{\lambda})=s_{\lambda}. \]
Este importante resultado nos permite definir las funciones de Schur a través del importante rol que juegan en la teoría de representaciones: Las funciones de Schur son las imágenes, bajo la aplicación de Frobenius, de las representaciones irreducibles.
El resultado anterior implica que ${\bf ch}$ es un isomorfismo de espacios vectoriales. La aplicación de Frobenius envía una base ortonormal de $CF^k$, los caracteres de las representaciones irreducibles de ${\mathbb{S}}_n$, en la base ortonormal de ${Sym}^{(k)}$ : las funciones de Schur. Concluimos entonces que la aplicación de Frobenius es una isometría.
Podemos utilizar la aplicación de Frobenius para obtener información sobre las funciones simétricas a partir de nuestros conocimientos de la teoría de representaciones del grupo simétrico. Por ejemplo, como es inmediato calcular los caracteres de las representaciones triviales y alternadas podemos concluir que
La primera afirmación es una consecuencia de la fórmula de inducción de Frobenius. La segunda se sigue inmediatamente de la definición del producto de Kronecker.
Sea $V$ un espacio vectorial de dimensión $m$. Escogiendo una base para $V$ identificamos $GL(V)$ con $GL_m(\mathbb{C})$. Sea $H$ el subgrupo de las matrices diagonales de $GL_m(\mathbb{C})$, y sea $diag(X)$ la matriz diagonal cuyas entradas en la diagonal principal son $(x_1, \cdots, x_n)$.
Un vector $v$ en una representacion $V$ se llama vector de peso, con peso $\alpha=(\alpha_1, \alpha_2, \cdots, \alpha_m)$, con coordenadas enteras, si \[ x \cdot v = x_1^{\alpha_1} x_2^{\alpha_2}\cdots x_m^{\alpha_m} v, \text{ para todo $x$ in $H$} \] Se tiene entonces que cualquier representación $V$ es una suma directa de espacios de peso $V= \oplus V_{\alpha}$, donde $V_{\alpha} = \{v \in V : x \cdot v = x_1^{\alpha_1} x_2^{\alpha_2}\cdots x_m^{\alpha_m} \, v, \text{para todo $x \in H$} \}$.
Una representación (finito-dimensional y holomorfa) $V$ de $GL_m(\mathbb{C})$ es irreducible si y sólo si tiene un único vector de peso $\alpha$ en la descomposición anterior. Más aún, dos representaciones son isomorfas si y sólo si tienen el mismo vector de peso. Hemos visto que las representaciones polinomiales de $GL(V)$ vienen indexadas por particiones, y se pueden construir a partir de las representaciones irreducibles del grupo simétrico.
El carácter de una representación (finito dimensional y holomórfica) $W$ de $GL(V)$, $Char_W=Char_W(x_1,\cdots,x_m)=\chi_W$ se define como la traza de $diag(x)$ sobre $W$.
Si descomponemos a $V= \oplus V_{\alpha}$ tenemos entonces que \[ \chi_V(x)=\sum_{\alpha}\dim(V_\alpha)x^\alpha=\sum_\alpha \dim(V_\alpha) x_1^{\alpha_1} x_2^{\alpha_2}\cdots x_m^{\alpha_m} \] Y en particular, para $V^{\lambda}$ tenemos un vector de peso para cada tableaux $T$ con entradas en $[m]$, de manera que \[ Char(V^{\lambda})=\sum X^T = s_{\lambda}(x_1, x_2, \cdots, x_m) \] es el polinomio de Schur indexado por $\lambda$.
En general, tenemos que \begin{align*} Char(W\oplus W') &=Char(W) \oplus Char(W')\\ Char(W\otimes W') &= Char(W) \, Char(W') \end{align*}
Definimos el anillo de representaciones de $ R(GL_m)$ como el grupo abeliano generado por las clases de isomorfía de las representaciones polinomiales de $GL_m$, junto con la operación de la suma directa.
Veamos que $R(GL_m)$ hereda de la operación de inducción entre representaciones del grupo simétrico una estructura de álgebra de Hopf con respecto al producto tensorial de representaciones.
Sea $X$ es una representación de ${\mathbb{S}}_n$ y $Y$ una representación de ${\mathbb{S}}_m$, hemos visto que $X \circ Y $ es una representación de ${\mathbb{S}}_{n+m}$ . Es sencillo demostrar que \[ \mathbb{V}(X\circ Y) \cong \mathbb{V}(X) \otimes \mathbb{V}(Y) \] Por lo que la operación de inducción de representaciones del grupo simétrico corresponde a tomar el producto tensorial de representaciones de $GL(E).$ Más aún, el problema de descomponer $S^{\lambda}\circ S^{\mu}$ como suma de representaciones irreducibles de ${\mathbb{S}}_{n+m}$, es equivalente al problema de descomponer $V^{\lambda} \otimes V^{\mu}$. En ambos casos los coeficientes de estructura que aparecen son los coeficientes de Littlewood-Richardson.
Esto evidencia una profunda relación entre las teoría de representaciones del grupo simétrico y del grupo lineal general, la llamada dualidad de Schur-Weyl. Sea $V$ un espacio vectorial de dimensión $m$. Recordemos que hemos definido sobre $V^{\otimes m}$ una estructura de $(GL(V), {\mathbb{S}}_n)$-módulo, donde el grupo $GL(V)$ actúa diagonalmente, y ${\mathbb{S}}_n$ actúa por la derecha. Estas dos acciones conmutan entre sí, y nos proporcionan la descomposición. \[ V^{\otimes m} = \sum_{\substack{\lambda\vdash n\\\ell(\lambda)\le m}} S^{\lambda} \otimes V^{\lambda} \] Esta descomposición nos proporciona una manera de estudiar las representaciones del grupo simétrico a través de aquellas del grupo lineal general, y viceversa. Por ejemplo, supongamos que queremos interpretar el producto de Kronecker, entre representaciones del grupo simétrico, en el lenguaje de la teoría de representaciones del grupo lineal general. Sea $V$ un espacio vectorial de dimensión $n$ y $W$ un espacio vectorial de dimensión $m$. Para hacer nuestra escritura más transparente, denotamos por $V^{\lambda}_m$ a la representación irreducible de $GL_m$ indexada por $\lambda$.
Tenemos entonces que $\dim(V\otimes W)=mn$ y \begin{align*} (V\otimes W)^{\otimes k} = \sum_{\lambda\vdash k, \ell(\lambda)\le nm} S^{\lambda} \otimes V^{\lambda} \end{align*} donde $V_{nm}^{\lambda}$ es la representación irreducible de $V\otimes W$ indexada por $\lambda$. Esta representación no es irreducible. Supongamos que se descompone de la forma: \[ V^{\lambda}_{n,m} = \sum _{\substack{\mu\vdash m, \ell(\mu)\le n\\ \nu \vdash m, \ell(\nu)\le m }} (V^{\mu}_n\otimes V_m^{\nu})^{g_{\mu,\nu}^{\lambda}}. \] Aplicando otra vez la dualidad de Schur-Weyl, a $ (V\otimes W)^{\otimes k}$, pero interpretando esta expresión como $V^{\otimes k} \otimes W^{\otimes k}$, obtenemos \[ V^{\lambda}_{n,m} = \big(\sum _{\mu\vdash k,\, \ell(\mu) \,\le n} V^{\mu}_n\otimes S^{\mu}\big)\otimes \big(\sum _{\nu\vdash k, \ell(\nu)\le m} V^{\nu}_m\otimes S^{\nu}\big) \] Todas estas ecuaciones son ciertas, módulo isomorfismo, así que podemos utilizar la propiedad conmutativa, junto con la descomposición del producto tensorial de representaciones irreducibles del grupo simétrico para concluir que los coeficientes $g_{\mu,\nu}^{\lambda}$ son precisamente los coeficientes de Kronecker.
Finalmente, podemos utilizar la dualidad de Schur-Weyl para interpretar los coeficientes de Kronecker en el lenguage de la teoría de representaciones del grupo simétrico. Los coeficientes $\gamma_{\mu,\nu}^{\lambda}$ describen la descomposición en irreducibles de la representacion $V^{\lambda}$ de $GL(V \otimes W)$ como suma de representaciones irreducibles de $GL(V)\times GL(W)$. Finalmente, utilizando la fórmula de reciprocidad de Frobenius podemos describir estos coeficientes en función de la operación de inducción.
Agradecemos a Emmanuel Briand por su apoyo y por varias discusiones matemáticas de gran utilidad.
[1] F. Ardila, E. León, M. Rosas, and M. Skandera, Tres lecciones en combinatoria algebraica. 1. Matrices totalmente no negativas y funciones simétricas, universo.math, vol.1 no.1 (2014) artículo 5.
[2] F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. II. Las funciones simétricas y la teoría de las representaciones, universo.math, vol.1 no.2 (2014)
[3] F. Ardila, E. León, M. Rosas, y M. Skandera. Tres lecciones en combinatoria algebraica. III. Arreglos de hiperplanos. 2013
[4] François Bergeron, Combinatoire algebrique, LaCIM, Universite de Quebec á Montreal. versión de 8 avril, 2001.
[5] W. Fulton, Young tableaux. With applications to representation theory and geometry. London Mathematical Society Student Texts, 35. Cambridge University Press, Cambridge, 1997.
[6] Bruce E. Sagan, The symmetric group. Representations, combinatorial algorithms, and symmetric functions. Second edition. Graduate Texts in Mathematics, 203. Springer-Verlag, New York, 2001.
[7] Richard P. Stanley, Enumerative combinatorics. Vol. 1. With a foreword by Gian-Carlo Rota. Corrected reprint of the 1986 original. Cambridge Studies in Advanced Mathematics, 49. Cambridge University Press, Cambridge, 1997.
[8] Richard P. Stanley, Enumerative combinatorics. Vol. 2. With a foreword by Gian-Carlo Rota and appendix 1 by Sergey Fomin. Cambridge Studies in Advanced Mathematics, 62. Cambridge University Press, Cambridge, 1999.
[9] Andrei V. Zelevinsky, Representations of finite classical groups. A Hopf algebra approach. Lecture Notes in Mathematics, 869. Springer-Verlag, Berlin-New York, 1981.



