

A todos nos ha pasado, tener la necesidad de saber si mañana, o en un par de días, lloverá o si hará frío. Consultamos el reporte meteorológico en el periódico, televisión o en alguna página de internet. Si bien es cierto que los pronósticos han mejorado mucho en los últimos años, también es verdad que siguen equivocándose, sobre todo en los pronósticos con varios días de anticipación.
¿Cómo predecir si mañana hará frío o calor? ¿Habrá viento o no? ¿Lloverá? Una manera de estudiar matemáticamente un fenómeno, digamos, $X$, que cambia con el tiempo, es utilizar ecuaciones diferenciales. Una ecuación diferencial nos indica cómo cambia $X$ en el tiempo. Se llama ecuación diferencial porque a los cambios de $X$ con el tiempo los llamamos derivada o diferencial. La ecuación relaciona esta derivada con otras cosas. ¿Qué cosas? Pues depende del tipo de ecuación.
La variable $X$ puede ser una función con valores reales, por ejemplo, la evolución de temperaturas en un cierto lugar, digamos $p$, o puede ser un vector, por ejemplo, la evolución de la temperatura, presión y humedad en el mismo punto $p$. La ecuación, puede en el primer caso depender sólo de la temperatura en el lugar o puede depender de todas las variables. Mas aún, hasta ahora, la variable $X$ era una función que dependía sólo del tiempo pero, es concebible que lo que pase en $p$ dependa también de lo que pase en un punto cercano $q$. De hecho puede depender no solo de lo que pase en el punto cercano, puede depender también de las diferencias de lo que esta pasando en los puntos. Por ejemplo si hay una diferencia de presiones entre los puntos podemos esperar un viento que tienda a nivelarlas. En términos matemáticos la ley depende no solo de los valores, como también de las derivadas espaciales.
En los primeros casos la incógnita es una función de una variable, la evolución en el tiempo de $X$, si es solo un número la llamamos ecuación diferencial ordinaria, si es un vector lo llamamos sistema de ecuaciones diferenciales ordinarias. En el ultimo caso la incógnita es una función que depende tanto del tiempo como del espacio, nos da las condiciones meteorológicas en cada punto y en cada momento. Se llama ecuación diferencial parcial por que la ley depende no solo de los valores de $X$ sino también depende de las derivadas parciales de $X$.
Con algunas excepciones, son mas fáciles de entender y resolver las ecuaciones que los sistemas, y son mas fáciles las ecuaciones ordinarias que las parciales. Como se imaginará el lector, al meteorólogo le tocó una de las más difíciles. Las siguientes animaciones nos muestran la riqueza y complejidad del fenómeno.
Aquí vemos los vientos:
Los modelos, es decir, las ecuaciones, usados por los meteorólogos incluyen además las complicadas interacciones de la atmósfera con los océanos.
Aquí vemos las corrientes:
En la página earth.nullschool.net se pueden encontrar, además, otros datos como la temperatura, la cantidad de nubes y muchas cosas más; y como cambian en tiempo real.
Plantear las ecuaciones diferenciales que determinan el tiempo no es una tarea fácil; mucho menos resolverlas, y esto es razón suficiente para convencernos de que el meteorólogo enfrenta un problema muy difícil. El propósito de este artículo es explicar porque, de hecho, su tarea, así planteada, es imposible. Las observaciones del clima podrán ser cada vez más precisas, las computadoras podrán ser más poderosas, nuestro entendimiento de los fenómenos relevantes podrá ser cada vez más completo; y en consecuencia, mejorarán los pronósticos de los meteorólogos. Sin embargo, por más que nos esforcemos, habrá un tiempo que, mas allá de él, los pronósticos no podrán ser certeros.
Edward Norton Lorenz, matemático que decidió dedicarse a la meteorología, simplificó el modelo meteorológico y se concentró en estudiar un problema aislado: la convección. Las partes bajas de la atmósfera son, por la radiación del suelo, mucho más calientes que las partes altas. El aire caliente sube, y el aire frío baja, pero ¿cómo es esta circulación? ¿cómo cambia la temperatura en determinado lugar a medida que el aire se mueve?
El modelo matemático de la convección se describe con dos ecuaciones parciales acopladas. Por un lado está el movimiento del aire, que obedece a la segunda ley de Newton: la fuerza es igual a la masa por la aceleración. En este caso las fuerzas que intervienen son: la gravedad, la diferencia de presiones y la viscosidad. Por otro lado, la temperatura cambia, en cada lugar, debido a que cuando el aire se mueve transporta el calor de donde estaba. En dinámica de fluidos la ley de Newton se llama la ecuación de Navier-Stokes y la segunda ecuación, la ecuación de transporte. La primera ecuación describe como se mueve un fluido y la segunda como cambia la temperatura. Están acopladas porque los resultados de una influyen en la otra y viceversa.
El modelo de la convección es mucho más sencillo que las ecuaciones completas de los meteorólogos, pero sigue siendo muy complicado. En particular, sigue siendo una ecuación diferencial parcial. Dado que se trata de un modelo donde hay oscilaciones, Lorenz se propuso buscar la solución en términos de sus coeficientes de Fourier; una suma, en principio infinita, de senos y cosenos de diferentes frecuencias, multiplicados por infinitos coeficientes. Es decir, redujo el problema a encontrar infinitas incógnitas: los coeficientes.
De todos estas incógnitas conservó solo los tres coeficientes más significativos y obtuvo un sistema de ecuaciones diferenciales ordinarias, que ahora llamamos las ecuaciones de Lorenz.
\begin{eqnarray*} \dot x & = & 10 (y-x ) \\ \dot y & = & 28 x -y -xz \\ \dot z & = & -\frac{8}{3}z+xy \end{eqnarray*}¡Finalmente una ecuación diferencial ordinaria! Una ecuación tratable, o eso pensábamos. El gran descubrimiento, y sorpresa de Lorenz fue que, aún en este modelo de juguete, con solo tres variables, se presenta un fenómeno incómodo para la predicción de resultados que se llama: sensibilidad a las condiciones iniciales. Esta propiedad garantiza que, dadas dos condiciones iniciales diferentes, arbitrariamente cercanas, producen soluciones que, en poco tiempo, describen situaciones muy diferentes.
Para entender un fenómeno complicado y desconocido, en general, conviene estudiar una versión muy simplificada, y conocida de él. Una simplificación más es suponer que el tiempo, en lugar de evolucionar de manera continua, lo hace de manera discreta; es decir, por unidad de tiempo. Pueden ser segundos, horas o décadas, no importa.
Para explicar la sensibilidad a las condiciones iniciales utilizaremos una versión ociosa de multiplicar números por $10$. Tomemos un número $x \in [0,1]$, que podemos suponer, describe algún fenómeno que estamos observando. Al transcurrir una unidad de tiempo, supongamos también, la evolución de dicho fenómeno está determinada por la siguiente transformación, o regla:
Lo primero que podemos observar es que si tomamos dos números muy parecidos, es decir, muy cercanos, digamos: $$0,{\bf018\,000\,5}14\,192\ldots \text{ y } 0,{\bf 018\,000\,6}98\,334\ldots $$ (difieren, a lo más, en una diezmillonésima parte de la unidad). Después de iterar 6 veces obtenemos: $$0,514\,192\ldots \text{ y } 0,698\,334\ldots, $$ que ya difieren en un décimo, pues la distancia entre ellos se multiplica por 10 en cada iterado. Iteramos una vez más, y obtenemos dos números completamente diferentes: $$0,141\,92\ldots \text{ y } 0,983\,34\ldots. $$ Esto no es una situación especial por los números que elegimos en el ejemplo. Dados dos números diferentes, no importa qué tan parecidos --qué tan cercanos--, después de iterar suficientes veces obtendremos resultados muy diferentes. Esta es la noción de la sensibilidad a las condiciones iniciales.
Visto de otra manera: si dos números no se alejan nunca, por más que iteremos la multiplicación por diez, entonces los dos números tendrán que ser iguales.
En este ejemplo no importa realmente que estemos multiplicando por diez, tendríamos un fenómeno muy parecido si multiplicamos por 2 solamente. Esta es la gráfica de dicha transformación:
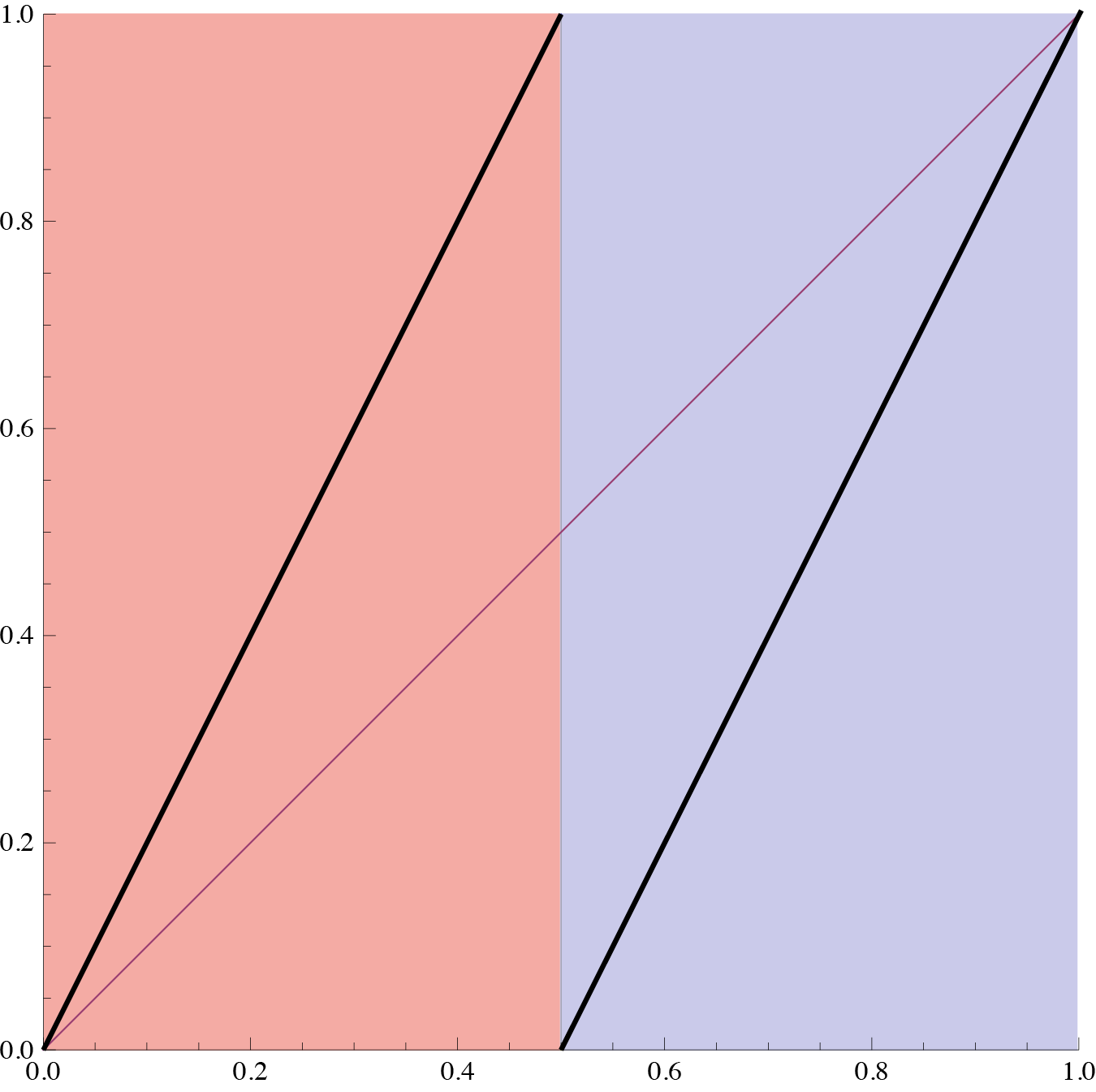
De hecho lo verdaderamente importante es que, en cada iterado la distancia entre puntos cercanos se multiplica por un factor mayor que 1. La gráfica podría ser algo como:
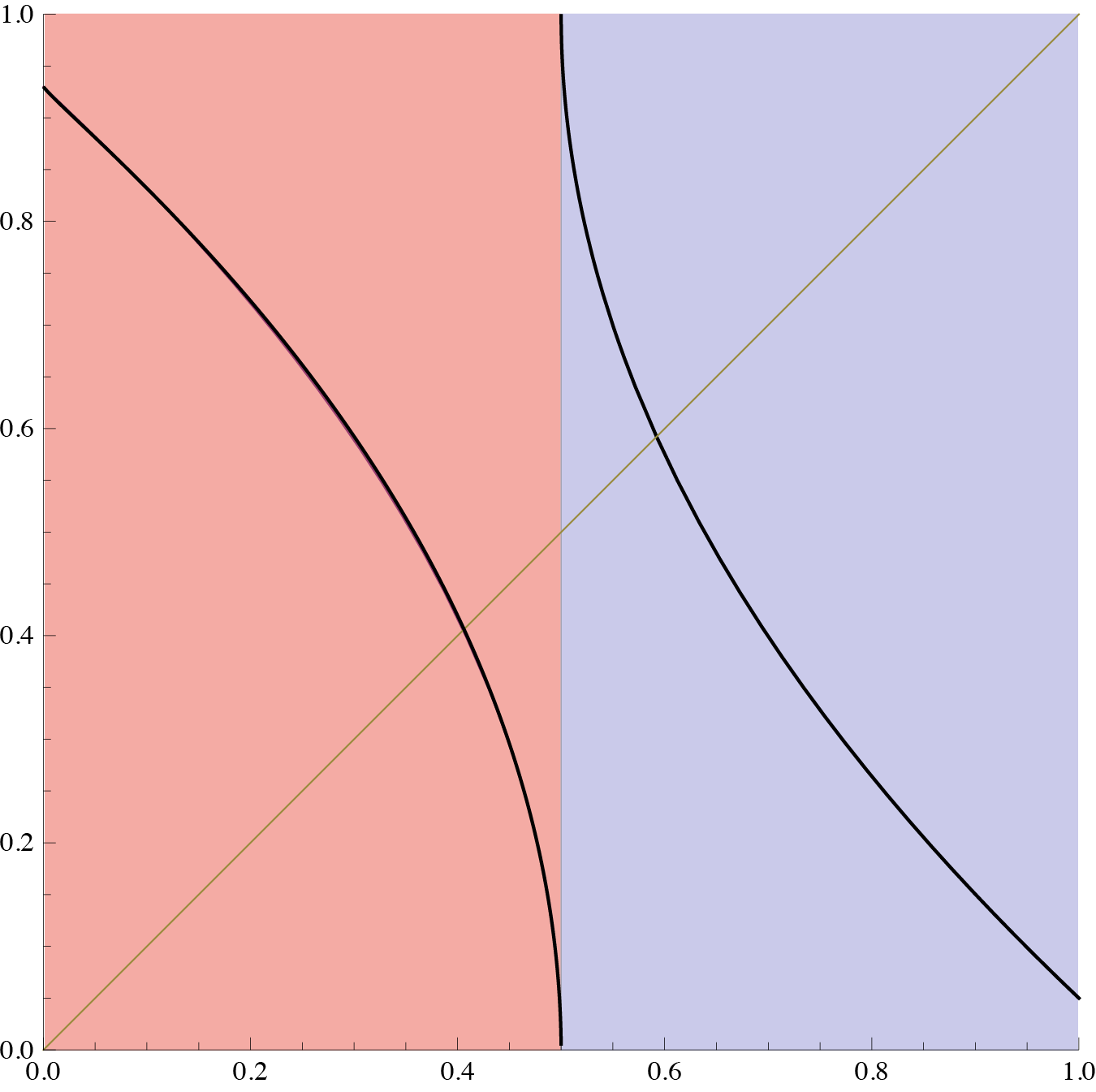
En todos los puntos, esta gráfica tiene derivada mayor que uno. Es decir en todos los puntos las distancias al aplicar la transformación, se agrandan, los puntos se separan.
y tendríamos las mismas conclusiones.
Nuestra tarea, ahora, es ilustrar que en las ecuaciones de Lorenz hay una gráfica parecida a la anterior, escondida, que gobierna la dinámica. Es decir, tenemos que mostrar como se pueden reducir la dimensión de un flujo en dimensión tres a una dinámica discreta de dimensión uno que expande. Para esto necesitaremos una combinación de argumentos locales con argumentos globales.
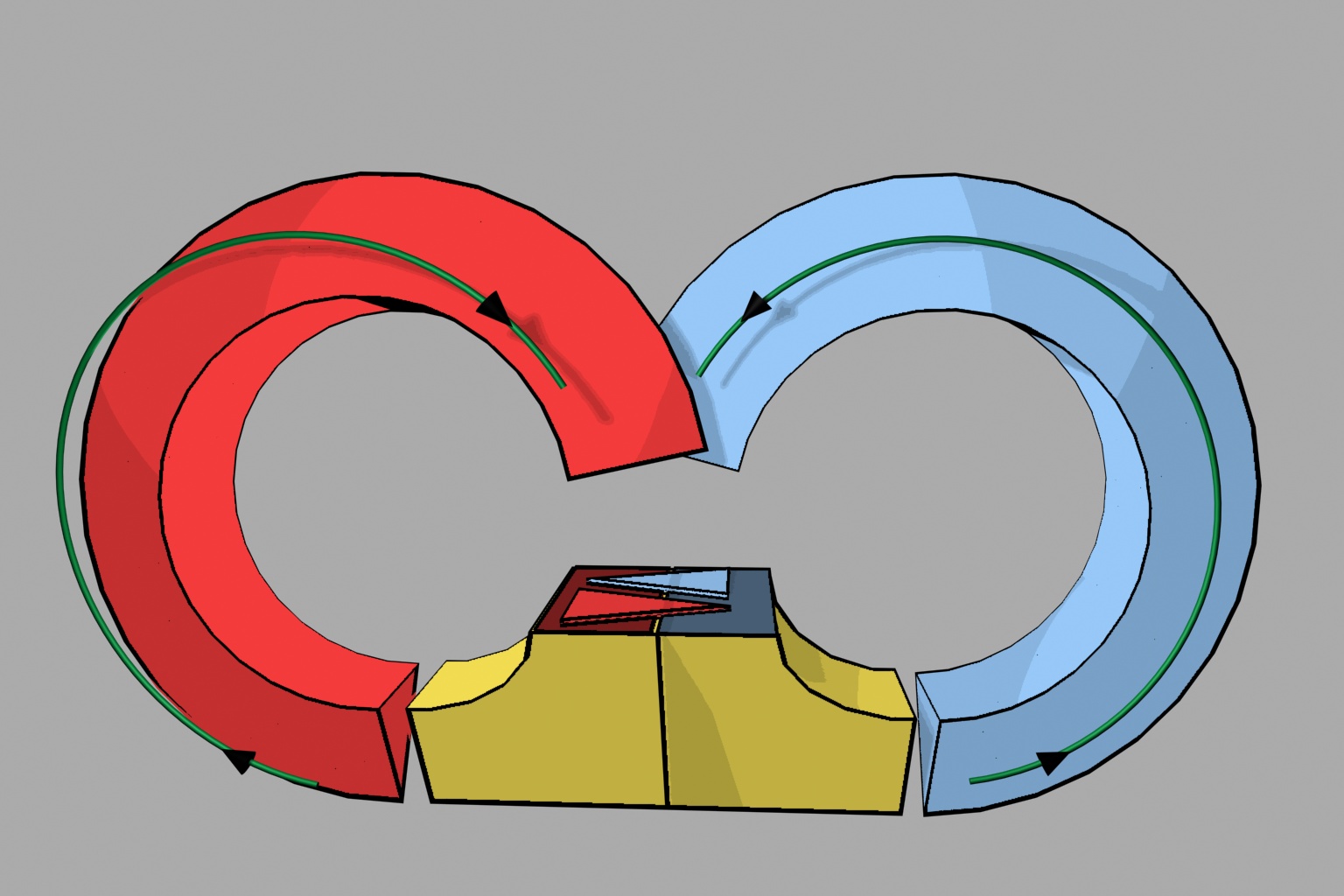
Una fuente imaginaria como esta:
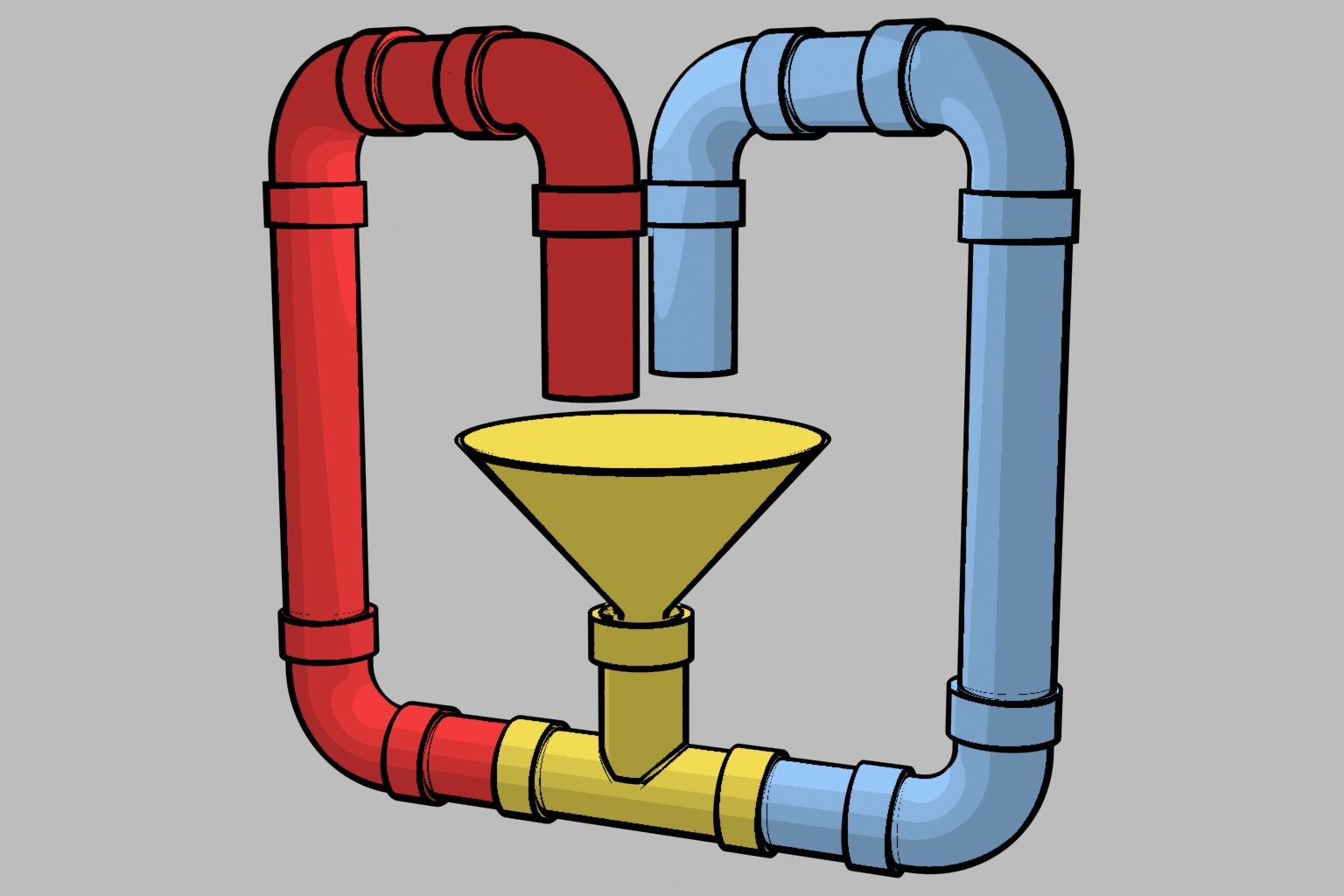
Fuente imaginaria. El agua circula continuamente por la fuente. Parte de ella por el tubo rojo, parte por el azul. Cada gota, al pasar por el embudo, tiene una misteriosa elección. Dos gotas cercanas en un momento dado pueden elegir tubos diferentes y tener recorridos muy diferentes.
captura muchas de las ideas involucradas.
Comencemos con la división de aguas. Las ecuaciones de Lorenz tienen al origen como punto de equilibrio, es decir, el origen es una solución trivial de las ecuaciones que no se mueve (el campo evaluado en el origen es cero). Lo que sucede en una vecindad del origen es muy parecido a lo que pasa con la parte lineal de la ecuación diferencial. Es fácil ver que la parte lineal en el origen tiene dos valores propios negativos $(\lambda_{ss} < \lambda_s < 0)$ y uno positivo $(\lambda_u>0)$. Es decir que existe un cambio de coordenadas donde la aproximación lineal es diagonal. En estas coordenadas, cerca del origen, las órbitas las gobiernan estas tres ecuaciones lineales desacopladas:
\begin{eqnarray*} \dot x & = & \lambda_u x \\ \dot y & = & \lambda_{ss} y \\\ \dot z & = & \lambda_s z \end{eqnarray*}Si el valor propio es positivo las orbitas, conforme el tiempo se va a infinito, se alejan del origen y si es negativo se acercan. Juntando todo en un dibujo obtenemos:
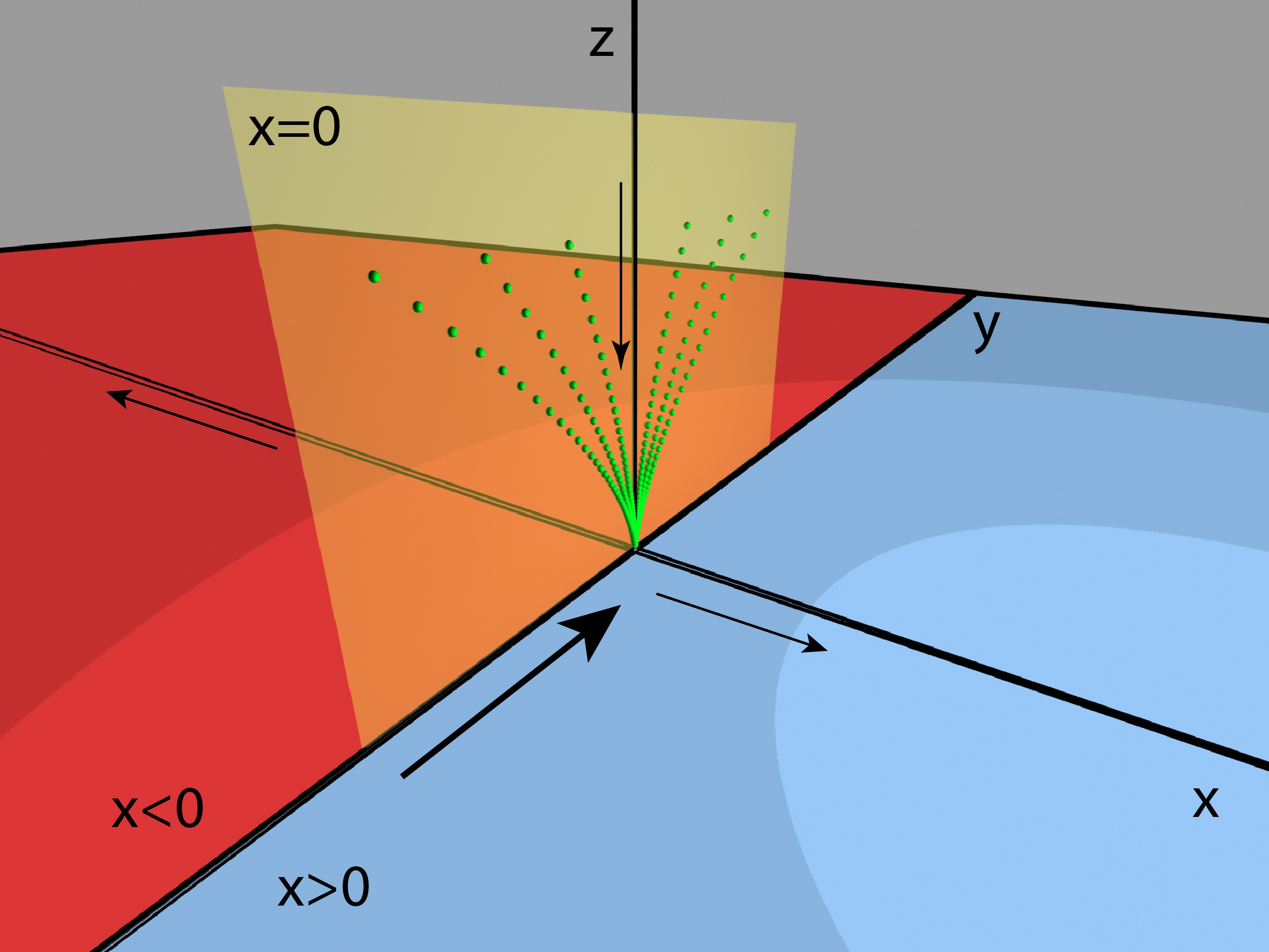
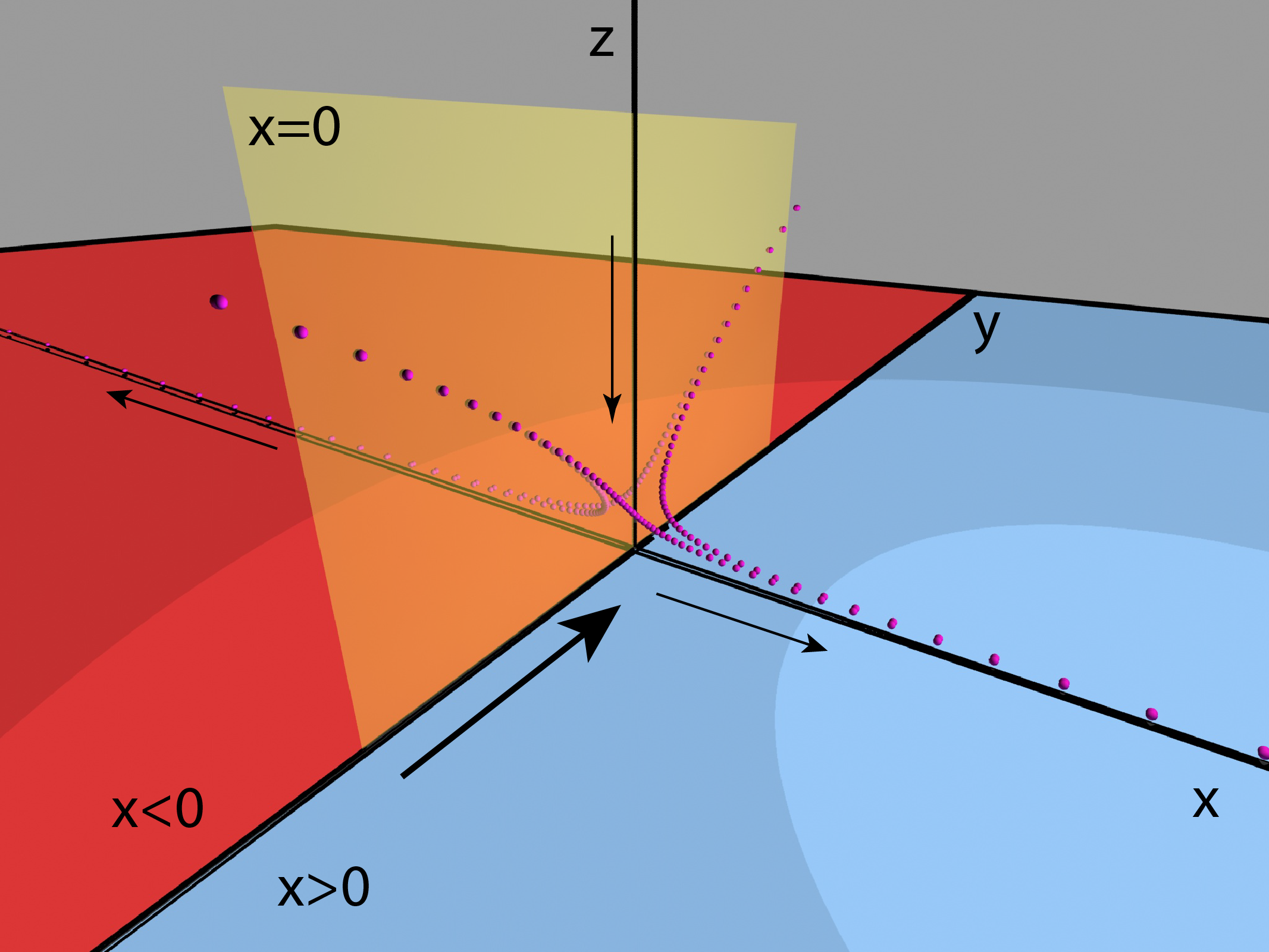
Observemos que:
En conclusión, la división de aguas es el plano $[x=0]$. Debemos de pensar, o imaginar, que estas ecuaciones lineales son las que modelan lo que ocurre en el embudo de nuestra fuente imaginaria.
Todavía podemos obtener más información de la parte lineal de las ecuaciones, pero para esto necesitamos introducir una sección de Poincaré.
En el ejemplo de la fuente, una sección de Poincaré sería una coladera debajo de los tubos, y encima del embudo, donde marcamos cada punto por donde una órbita pasa, en orden.
Para entender cualquier órbita dentro de la fuente basta describir por qué puntos de la coladera pasa y en qué orden; y no nos interesa saber el recorrido preciso dentro de la tubería.
Así, la evolución en el tiempo de nuestra fuente se describe como una transformación de la sección de Poincaré, determinada por la siguiente vez en la que cada punto de la sección regresa.
Esta transformación es la composición de dos transformaciones: la parte lineal, que corresponde al embudo y el pasaje a través del resto de la tubería.
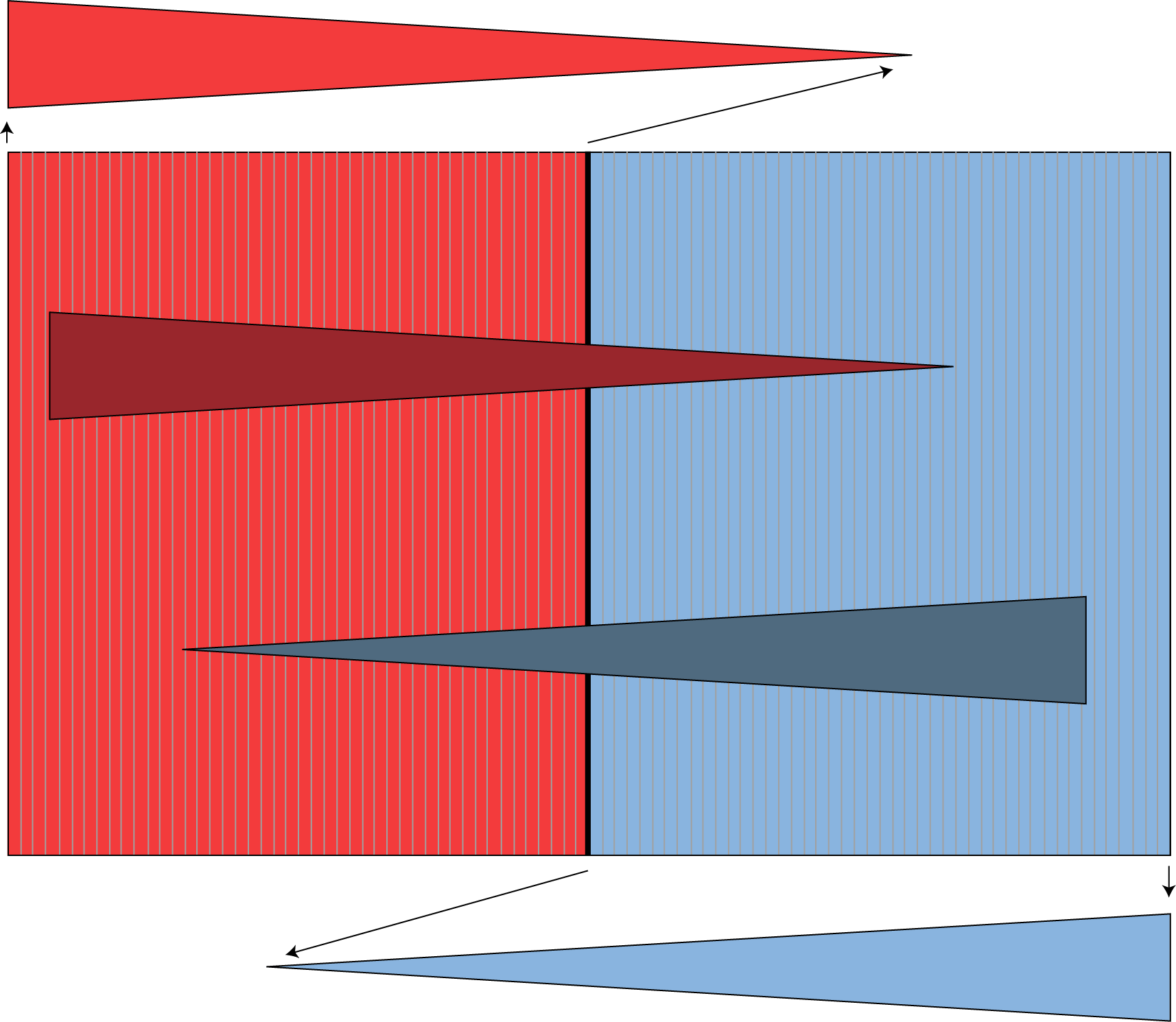
Agregamos la sección de Poincaré a nuestro dibujo, son dos rectángulos en el plano $[z=1]$ que comparten un lado:
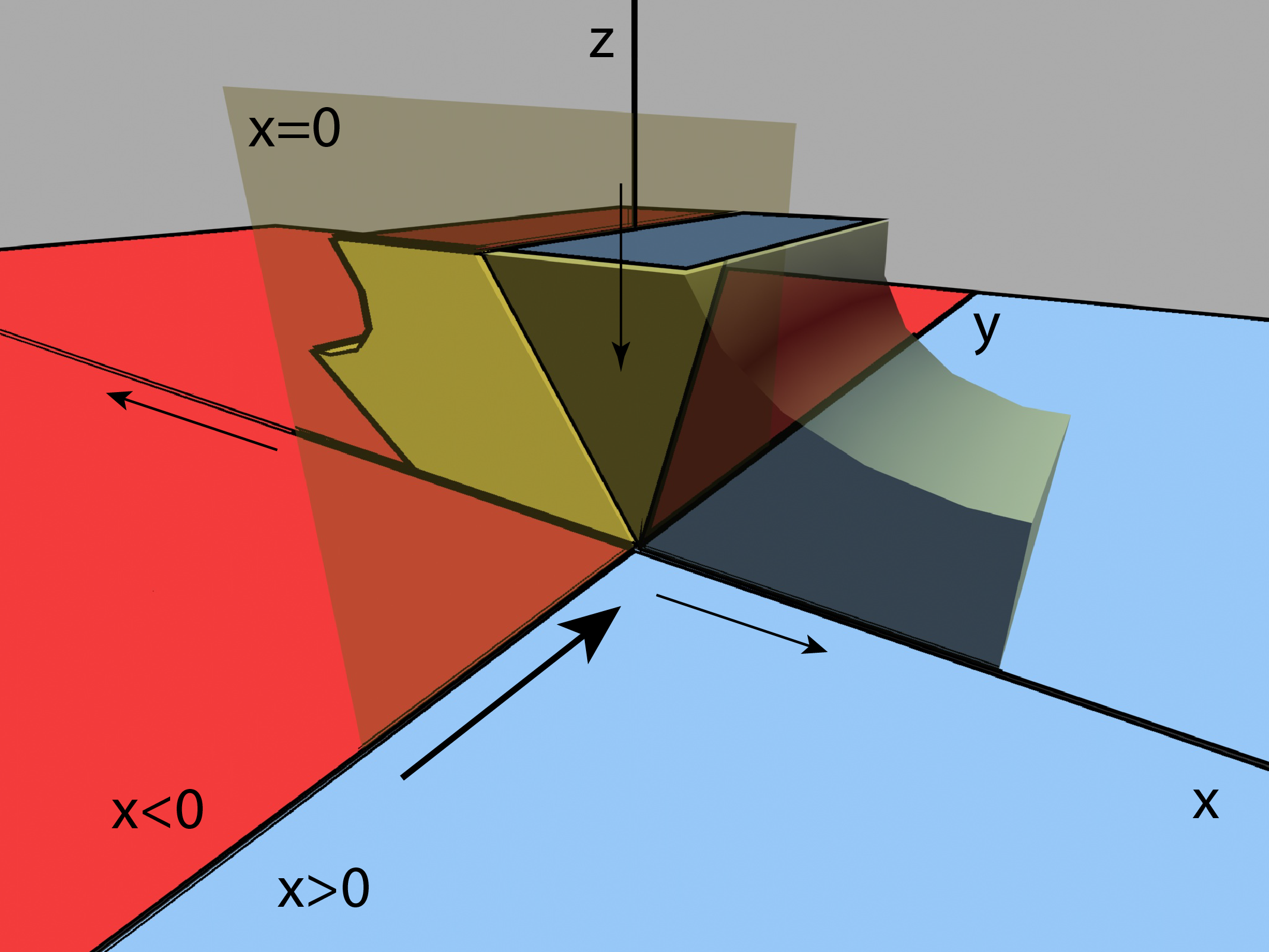
La sección de Poincaré, en el plano $[z=1]$, y sus imágenes en el pasaje por una vecindad del punto fijo.
Observe que el lado que comparten los rectángulos corresponde precisamente con la división de las aguas: los puntos cuya órbita converge al origen. Los demás puntos se alejan a la derecha o a la izquierda, de acuerdo al signo de su coordenada $x$.
Tomemos un punto que está del lado derecho (con coordenada $x > 0$). Su órbita en algún momento cruzará el plano $[x=1]$ en su viaje a $x \to +\infty$. El tiempo que tarda en llegar hasta ahí es variable y depende de que tan cerca del plano $[x=0]$ se encuentre. Análogamente, si el punto está del lado izquierdo (con coordenada $x<0$). Su órbita, cruzará el plano $[x=-1]$, en su viaje a $x \to -\infty$. Podemos escribir la transformación que asigna, a cada punto en el rectángulo $R$ su imagen en el plano $[x=1]$ o $[x=-1]$, de acuerdo al signo del valor de $x$. (Dejamos al lector interesado verificar que, efectivamente así se escribe esta transformación). $$(x,y,1) \mapsto ( \text{signo}(x) \cdot 1, y^{\frac{-\lambda_{ss}}{\lambda_u}}, x^{\frac{-\lambda_s}{\lambda_u}}),$$ donde $\text{signo}(x) = 1$ ó $-1$, de acuerdo a si $x$ es positivo o negativo.
En la figura arriba podemos ver que la imagen de cada uno de los rectángulos, el positivo y el negativo, son dos triángulos. Como en la dirección $y$ la contracción es más fuerte que en la dirección $z$ ($\lambda_ss < \lambda_s < 0$), los triángulos son oblicuos. Por otra parte, la altura de los triángulos está determinada por el cociente entre $\lambda_s$ y $\lambda_u$.
No cualquier silla hiperbólica funciona para construir una fuente en la que podamos encontrar fácilmente el fenómeno de la sensibilidad a las condiciones iniciales. Para esto es necesario que los valores propios $\lambda_s$ y $\lambda_u$ cumplan la siguiente relación: $$0 < \frac{-\lambda_s}{\lambda_u} < 1.$$ Bajo estas condiciones, la altura del triángulo crece: es decir hay un fenómeno de expansión muy parecido al de multiplicar por 10, como veremos más adelante.
Por otra parte, cabe resaltar una última propiedad de esta silla hiperbólica: los puntos en cualquier segmento de línea recta en $R$ con la misma coordenada en $x$ (lineas paralelas a la división de aguas) se acompañan en su pasaje y arriban, al mismo tiempo, a alguno de los planos $[x=\pm1]$ y dibujan una línea horizontal (coordenada $y$ constante). Esto es como si las coladeras imaginarias en los planos $[z=1]$ y $[x=\pm 1]$ tuvieran rejillas y el agua que pasa por una misma rejilla, $A$, sale por la misma rejilla $B$.
Esto reduce en una dimensión más el problema, pues la rejilla $A$ está dada por la coordenada $x$ y su imagen está determinada por su coordenada $z$, cuyo valor es $x^{\frac{-\lambda_s}{\lambda_u}}$; como $\frac{-\lambda_s}{\lambda_u} < 1$ la derivada, cerca del cero es uniformemente mayor que 1.
Volvamos al análisis global. Recordemos que la fuente tiene dos etapas: lo que pasa en el embudo y lo que pasa en las tuberías. Con la parte lineal hemos terminado de describir lo que sucede en el embudo: con nuestra elección de valores propios tenemos la expansión y con el truco de las rejillas redujimos la transformación a una dinámica unidimensional.
¿Qué pasa fuera de donde podemos aproximar por la parte lineal? Las ecuaciones de Lorenz son no-lineales en todos lados, pero cerca del origen se comportan muy parecido a la parte lineal del punto de equilibrio. En particular hay una variedad estable de dimensión dos, que en una vecindad del origen es muy cercana al plano $[x=0]$ y una variedad inestable de dimensión uno, cercana al eje $[x]$. Fuera de esta vecindad la variedad inestable ya no es una recta, y de hecho, regresa a la sección de Poincaré (coladera) de una manera muy parecida a la de las tuberías; y con ella regresan los dos pequeños triángulos.
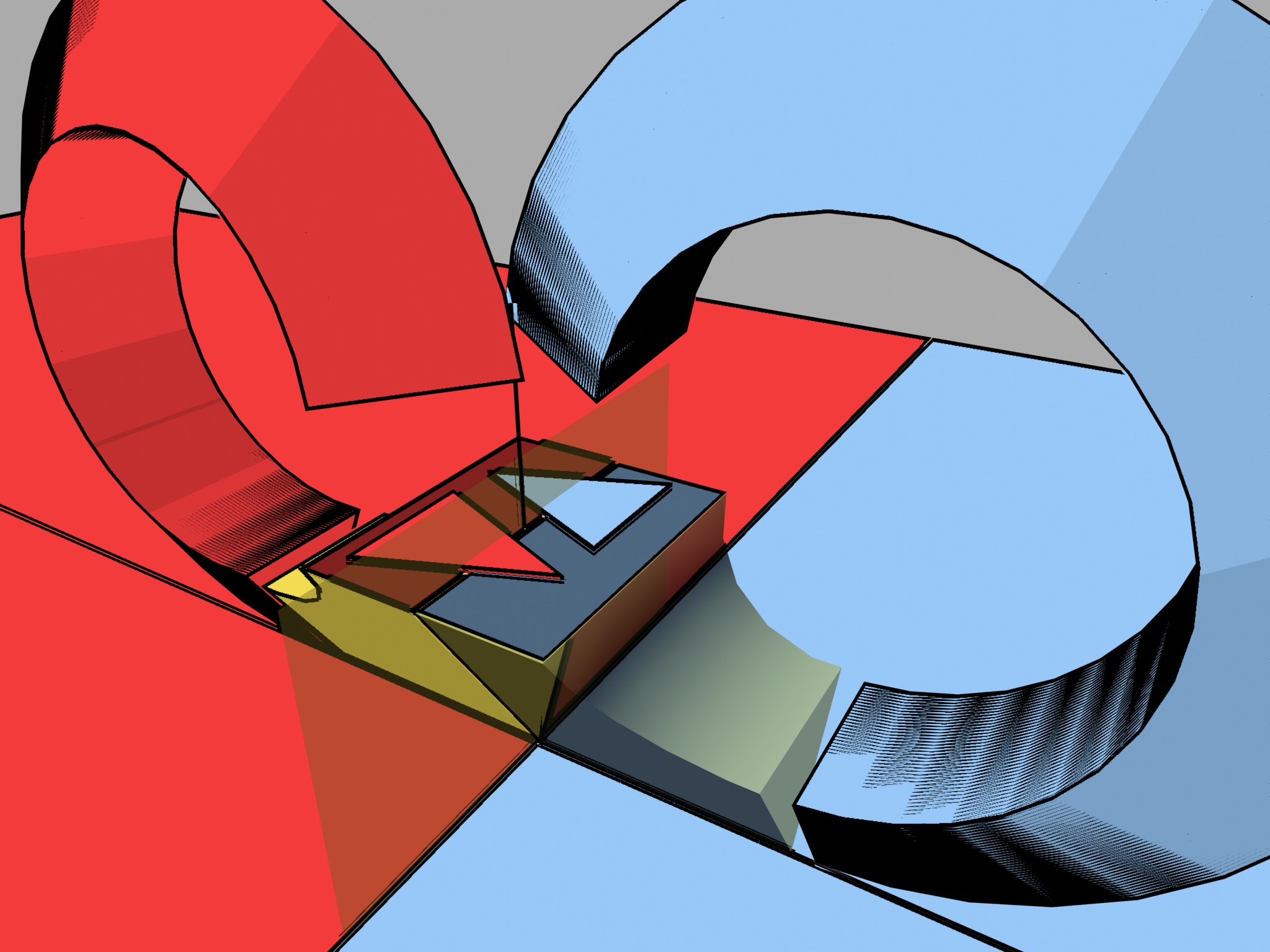
¿Podemos esperar conservar la expansión y la reducción de dimensión, al pasar por esta parte no lineal? La expansión es más fácil, la parte no lineal puede tener un poco de contracción, pero es una fija. En el origen la derivada es infinito, en un rectángulo pequeño, la derivada es enorme, la expansión es enorme y compensa cualquier posible contracción de la parte no lineal.
Para preservar la dinámica unidimensional es necesario demostrar la existencia de una foliación invariante (rejillas van en rejillas), esto no es fácil de probar. John Guckenheimer y Robert F. Williams, en la década de los 70's asumieron que existía tal foliación y construyeron lo que llamaron el Lorenz geométrico, Tuvieron que pasar treinta años para que Warwick Tucker probara que, en efecto, en las ecuaciones que Lorenz dicha foliación invariante está presente.
En conclusión: en las ecuaciones de Lorenz tenemos el fenómeno de la sensibilidad a las condiciones iniciales, con sus consecuencias funestas al respecto de la predictibilidad.
¿Qué podemos decir entonces si queremos describir la dinámica de multiplicar? ¿si queremos describir la dinámica de las ecuaciones de Lorenz? si ya sabemos que todas las dinámicas son posibles? ¿Si tenemos sensibilidad respecto a las condiciones iniciales? ¿Si parece moverse al azar? Afortunadamente el ingenio humano es tan grande que no quedamos en la impotencia de la ignorancia absoluta. Lo primero que podemos decir es pues precisamente esto: ¡Se mueve como si fuera al azar!
Somos capaces de cambiar las preguntas que ya no tienen sentido como: ¿Por dónde va estar el sistema dentro de 25 iteraciones? a otras que sí lo tienen como: ¿cuál es la probabilidad que este del lado derecho o izquierdo?
Algo sorprendente que se observa es que podemos empezar de casi cualquier punto y las propiedades estadísticas de la órbita serán las mismas. Lo que esto significa es que casi todas las órbitas convergen a un mismo objeto, a un atractor. Lo que observamos al realizar análisis numérico de las ecuaciones lineales son, en realidad, las propiedades estadísticas del atractor. Así, el nuevo motivo de estudio no son los detalles de un sistema, de sus evoluciones, sino las propiedades estadísticas de sus atractores. Este es un gran cambio de perspectiva de lo que quiere decir resolver.
¿Qué hay del meteorólogo, él puede también cambiar de perspectiva? Sí y en ese caso se llama, climatólogo. Entender el clima en la época de ultima glaciación no quiere decir cual era la temperatura hace exactamente 10 mil años. Quiere decir, más bien, cuál era el promedio, cual era la temperatura probable cual era la desviación, etcétera.
De la misma manera entender como será el clima en cien años, si seguimos aumentando los niveles de dióxido de carbono en la atmósfera, quiere decir como cambia una medida invariante cuando cambian los parámetros del sistema. Pero dejemos este tema para una futura colaboración.

Aubin Arroyo nació en la ciudad de México y estudió la carrera de matemáticas en la Facultad de Ciencias de la UNAM. Viajó a Río de Janeiro a estudiar el doctorado en el IMPA y desde 2002 trabaja en la Unidad Cuernavaca del Instituto de Matemáticas de la UNAM, en problemas relacionados con los Sistemas Dinámicos.

Renato Iturriaga estudió la licenciatura y la maestria en la facultad de ciencias de la UNAM. Su doctorado lo hizo en sistemas lagrangianos bajo la dirección de Ricardo Mañe, en el IMPA en Rio de Janeiro. Desde 1994 trabaja en el CIMAT en problemas relacionados con dinamica conservativa.