Un teorema y una "conjetura" de Marco

Nos enteramos con consternación del fallecimiento del matemático Marco Brunella. Para rendirle homenaje en un sitio dedicado a las matemáticas, propongo escribir sobre uno de sus teoremas y una de sus conjeturas.

Me encontré con Marco en Rio en 1993 mientras él hacía una estancia postdoctoral. La claridad de su visión matemática me impresionó inmediatamente. Enseguida colaboramos y recuerdo la redacción del artículo que escribimos juntos entonces. ¡Él italiano; yo francés; hablábamos en portugués entre nosotros y escribíamos en inglés! Marco buscaba acortar el texto, restringirlo a lo estrictamente necesario, mientras que yo proponía que repitiéramos cosas para que el lector pudiera comprender mejor. ¡Pero Marco permanecía inflexible! Sus textos eran, a su imagen y semejanza, de una gran sobriedad.

He aquí uno de los problemas más antiguos en mecánica. La figura siguiente representa una palangana:

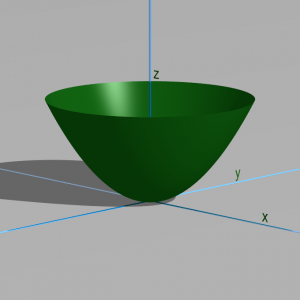
Si ponemos una bola en el fondo de la palangana, pues ahí se queda ... sin moverse. Si le damos un golpecito a la bola, es claro que oscilará alrededor de la posición de equilibrio sin alejarse mucho. Decimos en este caso que la bola está en un mínimo del potencial, en una posición de equilibrio estable. El hecho de que un mínimo sea siempre una posición estable es un teorema de Lagrange, concretado más tarde por Dirichlet.

Por el contrario, si ponemos una bola en la cima de una montaña, ésta estará en equilibrio ... inestable. Una mínima perturbación a la bola, un pequeño soplo de viento y la bola rueda cuesta abajo. Un máximo del potencial es inestable.

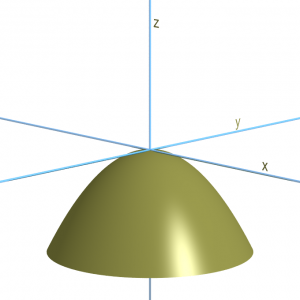
En la figura siguiente, que representa una silla de montar, no se trata ni de un máximo ni de un mínimo.

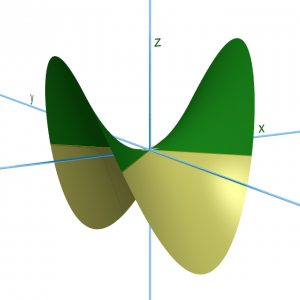
Aquí también parece claro que hay inestabilidad: si empujamos ligeramente la bola, en la buena dirección, ésta cae en el valle. Observa ahora esta situación:

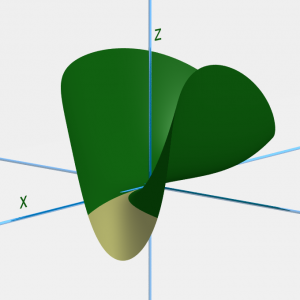
Constatamos que la zona amarilla, allí donde uno se encuentra bajo el nivel del punto de equilibrio, tiene una forma puntiaguda y ligeramente torcida. ¿Es inestable el equilibrio? ¿No podríamos imaginar que la bola que rueda cuesta abajo sea, de cierta manera, expulsada de la zona amarilla por una "fuerza centrífuga" que la haría volver a subir encima del punto de partida, asegurando así estabilidad?

Muchas obras de física afirman, sin demostración, que no puede haber estabilidad a menos de que haya un mínimo. ¿Tienen razón? En el ejemplo anterior, sería fácil demostrar que el equilibrio es inestable y que la bola puede en efecto rodar cuesta abajo.

Nace entonces la pregunta sobre el recíproco del teorema de Lagrange-Dirichlet. Hubo que esperar a 1977 para que Palamodov demostrara finalmente dicho recíproco ... para potenciales que dependen sólo de dos variables ((x,y) en nuestras figuras). Si el potencial depende de más variables, el mismo Palamodov afirma haber demostrado el teorema en 1995 pero no publicó más que un esbozo de prueba que no parece convencer para nada a los especialistas. Según algunos, el recíproco del teorema de Lagrange-Dirichlet sería todavía un problema abierto.

Marco retomó el problema posicionándolo en un contexto bastante más general, liberándolo de alguna manera de sus aspectos mecánicos. Se trata de las ecuaciones diferenciales. Consideremos un punto del plano $(x,y)$ que evoluciona a lo largo del tiempo según la ecuación diferencial:

Las soluciones a estas ecuaciones son explícitas:

En el plano, éstas son círculos concéntricos. Si la curva parte de una posición inicial cercana al origen, ésta no se aleja. El origen es una posición de equilibrio estable.

El teorema que quisiera describir concierne el caso de la dimensión 3. Se considera la ecuación diferencial:

Hacen falta, por supuesto, hipótesis para un teorema. Suponemos que $P,Q,R$ son polinomios que se anulan en el origen $(0,0,0)$. El origen es, entonces, un punto de equilibrio para la ecuación: ¡un punto que parta de éste se queda ahí! Suponemos, igualmente, que, en una vecindad del origen, no hay otro punto de equilibrio. ¡Entonces el teorema afirma que el origen es inestable! Esto significa que podemos encontrar puntos arbitrariamente cercanos al origen que se alejan de manera significativa después de un cierto tiempo, en el futuro o en el pasado. Más precisamente, éste establece la existencia de una posición inicial $(x_{0},y_{0},z_{0})$ cercana al origen (y diferente de éste) tal que $(x(t),y(t),z(t))$ tiende a $(0,0,0)$, bien sea cuando $t$ tiende a más infinito o cuando $t$ tiende a menos infinito. Podemos presentar las cosas de otra manera. Si un punto parte de $(x(t),y(t),z(t))$, entonces después de un tiempo $-t$ se encuentra en $(x_{0},y_{0},z_{0})$. Como $(x(t),y(t),z(t))$ está arbitrariamente cerca del origen, esto implica la inestabilidad anunciada.

El enunciado es simple y la prueba, elaborada. El lector puede echarle un ojo al artículo.

La misma prueba, ligeramente adaptada, demuestra el teorema de Palamodov, es decir el recíproco del teorema de Lagrange-Dirichlet para los potenciales que depende de dos variables.

Vimos que una ecuación diferecial puede ser estable en dimensión 2 y que siempre es estable en dimensión 3. ¿Cómo es en dimensión superior? Ésta es la conjetura de Brunella: una posición de equilibrio aislada de una ecuación polinomial en dimensión impar siempre es inestable.

No puedo explicar aquí el vínculo entre la conjetura de Marco y el recíproco del teorema de Lagrange-Dirichlet. Me contentaré con hacer la siguiente observación. Si un punto en el espacio de dimensión $n$ se desplaza, su posición depende de $n$ números así como de su velocidad, lo que da un total de $2n$ números para describir al par posición/velocidad. La preservación de la energía total — suma de la energía cinética y de la energía potencial — impone una condición, de modo que la dinámica se desarrolla en un espacio de dimensión $2n-1$, un número impar.

Es el momento de comentar sobre el uso de la palabra "conjetura". No es raro que un matemático proponga un enunciado que piense que es cierto pero que no sepa demostrar. A veces, lo enuncia con fuerza bautizándolo "conjetura". Otras veces, de manera más modesta, se contenta con presentarlo como una simple pregunta. Acto seguido, otros matemáticos pueden promover el enunciado al rango de conjetura. Es lo que acabo de hacer con la conjetura sobre las ecuaciones diferenciales. Marco, con la sobria escritura que lo caracterizaba, se contentó con hacer una observación entre paréntesis. Después de haber recordado el concepto de estabilidad de una posición de equilibrio, añade en dicho paréntesis que no conoce ningún ejemplo en dimensión impar ("we don't know any").

Sólo un ejemplo de un resultado de Marco, entre tantos otros.

Sobriedad y concisión son las dos palabras que me vienen a la mente cuando pienso en Marco.