

El balón oficial de la copa mundial de fútbol oficialmente se dio a conocer en diciembre 2013.
Después de una gran consulta nacional en Brasil, se decidió que se llamaría "Brazuca", un apodo que significa "brasileño".

Quisiera revelar aquí una verdad que las presentaciones del Brazuca parecen esconder:

¿Increíble, no?
Aquí está la foto de los balones oficiales de las copas del mundo desde 1970. Por supuesto, se trata de que parezcan mas originales comparados con los anteriores, pero debo decir que la idea de un balón cúbico es toda una pequeña revolución futbolística.

Se recortan una serie de piezas (antes de cuero y, hoy en día, de polietileno) y se cosen o se pegan para hacer una bola lo más esférica posible. Adentro, se infla una cámara de aire para que la presión mejore la redondez del balón.
Las piezas se recortan de un material plano. Quizás, para la Copa 2018, se podrán producir directamente piezas esféricas; sin embargo, éste no parece ser el caso.
La primera idea es hacer un poliedro (el cual se obtiene pegando polígonos). Es claro que, para que el poliedro "tenga un aspecto más redondo", debe tener muchas caras; mientras más pequeñas, mejor. También es claro que la forma de estas caras debe ser tan regular, tan simétrica como sea posible. Un buen balón (bien redondo) debe verse igual, independientemente del entorno en el que se observa.
Gracias a Platón, sabemos que sólo hay cinco poliedros regulares: el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro, con 4, 6, 8, 12 y 20 caras, respectivamente.
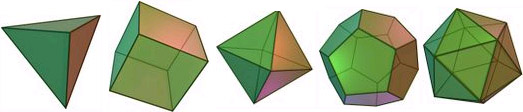
Así, uno inicialmente escoge el poliedro que tiene más caras: el icosaedro con 20 caras (que son triángulos equiláteros). Para mejorar aún más la redondez, se puede tratar de cortar las esquinas; es decir, truncar el icosaedro. Para cada vértice, imaginen los planos perpendiculares a la recta que lo une con el centro. Cuando el plano se encuentra cerca del vértice, el icosaedro se corta en un pequeño pentágono y las caras triangulares se convierten en hexágonos (cuyos tres lados son pequeños). Cuando el plano se desplaza hacia el centro, los pequeños lados de los hexágonos aumentan: llega un momento en que todos los hexágonos y pentágonos se vuelven regulares. Ésta es la forma tradicional de una pelota de fútbol: un icosaedro truncado con 20 caras hexagonales y 12 caras pentagonales.
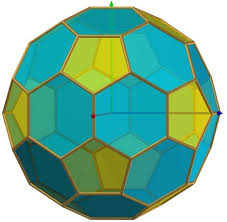
En un artículo en Images des Maths todo esto se describió antes de la Copa Mundial anterior. Si quieren aprender a dibujar estos ico-dodeca-edros, una bonita nota en IdM les puede ayudar.

Para las pelotas de tenis, y otros balones, vean esta nota.
Obviamente, la evolución tecnológica de los balones no se limita a su geometría: no hace falta decir que la forma de coser o pegar las piezas del rompecabezas también ha cambiado mucho.
El balón estándar (icosaedro truncado) se forma de polígonos planos que se pegan entre sí sin deformarse ni torcerse. Inflados, ya tienden a tener una forma esférica (pero esto es otra historia).
Para el Brazuca, aunque las piezas también son planas, se "doblan" al ensamblarlas, y después se estiran de nuevo al momento de inflarlas.
Veremos esto con un poco más detalle.
Al cortar un trozo de papel, éste se puede deformar en el espacio de muchas maneras, sin romperse. En geometría, uno habla de superficies "desarrollables".
Aquí hay un ejemplo:

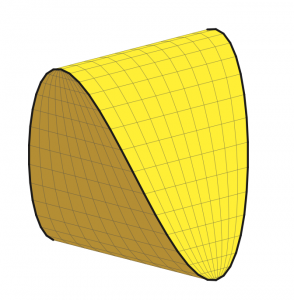
Uno puede imaginar poliedros cuyas caras no son polígonos planos, sino superficies desarrollables, que, por tanto, se pueden cortar en papel antes de ensamblarse. Éste es un ejemplo de un poliedro curvo:

Con las caras que no son necesariamente planas, ¿se podrán producir poliedros más redondos? ¿Por qué no los balones de fútbol?
Comencemos con un ejemplo sencillo.
Una región es convexa si cualquier segmento que une dos de sus puntos está contenido completamente dentro de la región.
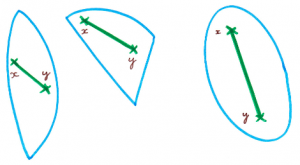
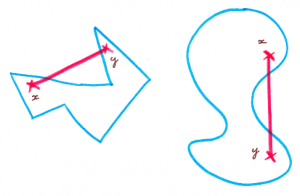
Consideremos ahora dos regiones convexas en el plano cuyos bordes son de la misma longitud. Recortemos estas regiones de papel, escojamos un punto sobre el borde de cada una de ellas y peguemos estos puntos.

Después, con una cinta adhesiva o con el pegamento, procedamos a pegar los bordes de las dos regiones. Pogorelov demostróPogorelov, Extrinsic geometry of convex surfaces, AMS, 1973. en los años setenta que esto siempre se puede hacer sin que se formen plieges que lo impidan. Así produciremos un objeto en el espacio y Pogorelov demostró que este objeto será convexo como un cuerpo tridimensional; ¡esto no es de todo obvio! Se podría imaginar que no siempre se pueden pegar las dos regiones sin romperlas en alguna parte. Y no hay ninguna razón a priori para pensar que el objeto construido será convexo.
El objeto que acabamos de construir consiste de dos superficies desarrollables, pegadas a lo largo de sus bordes.
Este artículo en IdM ilustra el teorema de Pogorelov con un ejemplo sencillo: la pelota de tenis.
Mejor aún.
En lugar de usar dos regiones, se puede, por ejemplo, comenzar con seis regiones convexas, pensando en ellas como "caras cuadradas" de un cubo. En los bordes de cada una de estas regiones, se escogen cuatro puntos, pensados como los vértices del "cuadrado". Se supone que las cuatro "esquinas" escogidas son, de hecho, esquinas, es decir, que las regiones tienen ángulos en estos puntos.

Supongamos que las longitudes de todos los "bordes curvos" son las mismas. Entonces, tomemos la cinta adhesiva y peguemos las seis regiones, como para hacer un cubo.
Para que recuerden, ¡les muestro un cubo!
Se requiere aún otra hipótesis: cada vértice de un cubo pertenece a tres lados distintos. Se necesita que la suma de los tres ángulos correspondientes sea menor o igual a 360 grados.
El teorema de Pogorelov asegura que, bajo estas hipótesis, ¡todo funciona! Así obtenemos una especie de cubo, con bordes curvos, y cuyas seis caras son desarrollables pero no necesariamente planas.
¡Aún más fuerte!
Para poder aplicar el teorema no es necesario requerir que las regiones sean convexas. La condición importante es que cuando se unan las dos puntos, la suma de las curvaturas de las dos regiones en cada punto de contacto sea positiva. En términos menos precisos, debemos pegar una concavidad con una convexidad más fuerte.

El Brazuca se fabrica usando el teorema de Pogorelov. Aquí están las seis caras "cuadradas" que se juntan para producir un "cubo esférico":

Notemos que cada pieza tiene, en efecto, cuatro "esquinas" pintados en negro. El ángulo en cada esquina es de 120 grados.
Así es como se unen las seis superficies desarrollables:

Aquí vemos un "vértice" del cubo: allí se juntan tres caras, como debe ser en un cubo. En total, hay seis caras y ocho vértices. Notemos que los tres ángulos de 120 grados dan un total de 360 grados, un círculo completo, por lo que el Brazuca no presenta un "vértice agudo", como en el caso de un cubo normal.

Y aquí hay unas fotos para ilustrar la estructura cúbica.




Y ¡voilá!
No obstante, hubo que encontrar estas formas, que, además de verse bien, producen un balón casi perfectamente esférico.
Este video muestra la fabricación del Brazuca:
Sorprendentemente, al mismo tiempo que los ingenieros de Adidas estaban diseñando el Brazuca, el gran matemático W. Thurston llegó a la misma idea, pero por un camino distinto.
Thurston, al igual que muchos geómetras del pasado, ¡estaba interesado en la forma de cortar la ropa para cubrir la superficie del cuerpo humano! En uno de sus últimos artículos, escrito en colaboración con Kelly Delp, él explica sus ideas y sus fracasos. Como buen matemático teórico, asume que la superficie que hay que vestir es perfectamente esférica. Partiendo del octaedro, busca una forma para las caras triangulares con el fin de que el objeto obtenido sea el más esférico posible.
Aquí están los ocho "triángulos" que él propone:

Y aquí está el resultado:

Al final, esto se parece mucho al Brazuca, ¿verdad?
Estoy maravillado por el ingenio de los ingenieros de Adidas que simplemente han "redescubierto" el teorema de Pogorelov: estoy seguro de que no lo conocían (e incluso de que todavía no lo conocen).
¡Estoy igual de maravillado por la creatividad de Delp y Thurston que buscaron la inspiración en la moda!
Para hacer matemáticas, ¿es útil conocer la obra de los predecesores? La cuestión es complicada. Por supuesto, si nadie estudiara lo que han hecho los geómetras del pasado, no llegaríamos muy lejos... Por otro lado, para apropiarse de las cosas del pasado a veces es útil descubrirlas por tu propia cuenta.
CUIDADO CON LAS IMITACIONES: he visto aquí en venta un Brazuca falso. Se ve bien que es un icosaedro truncado bajo la apariencia de un cubo. ¡No lo compren!

Étienne Ghys es un matemático francés. Trabaja principalmente en geometría y sistemas dinámicos, aunque sus intereses matemáticos son amplios. También se ha interesado por el desarrollo histórico de las ideas matemáticas, en particular, por la contribución de Henri Poincaré. Ha sido coautor de la película animada por computadora Dimensions: ¡Un paseo a través de las matemáticas!.
Graduado de la École normale supérieure de Saint-Cloud, en la actualidad es un "directeur de recherche" de CNRS en la École normale supérieure en Lyon. También es el editor-en-jefe de Publications Mathématiques de l'IHÉS y miembro de la Academia Francesa de Ciencias.
(Traducido de Wikipedia).