

Las leyes de Kepler describen el sistema solar como un mecanismo. Los planetas siguen trayectorias definidas por unas reglas completamente misteriosas:
Kepler dedujo sus leyes de las observaciones y, al no poder explicarlas, sólo pudo expresar su admiración ante hechos tan maravillosos en sus libros Mysterium cosmographicum, Astronomia nova y Harmonices mundi (de hecho, no había manera de derivarlas en aquel entonces: las leyes de Newton se descubrirían unos 80 años después). Kepler también creía que el movimiento de los planetas se relacionaba con la armonía musical, acorde con el concepto filosófico antiguo de la música universal o celeste.
Varias de la hipótesis de Kepler fueron posteriormente refutadas. La supuesta relación entre las órbitas de los planetas y los sólidos platónicos o la música no tiene sustento en el conocimiento moderno. Sin embargo, las obras de Kepler son la cumbre de la ciencia de su tiempo y los dibujos que las ilustran son unas joyas del arte científico. Sugieren una idea que resultó ser de gran importancia en la física: la simetría tiene un papel clave en el diseño del mundo.
La mecánica de Newton da un fundamento a las observaciones principales de Kepler. En la primera aproximación, el movimiento de un planeta alrededor del Sol es ejemplo de un sistema de dos cuerpos que se atraen con una fuerza inversamente proporcional al cuadrado de la distancia entre ellos. El movimiento de cada cuerpo en tal sistema se puede describir como el movimiento en un campo de fuerza central con el potencial $-k/r$, donde $k$ es una constante positiva, y $r$ es la distancia al centro de masas del sistema. La segunda ley de Newton da, entonces, una ecuación diferencial de segundo grado cuya solución describe el movimiento del planeta. Así, en principio, se pueden demostrar las primeras tres leyes de Kepler; sin embargo, la manera más elegante de hacerlo involucra las leyes de conservación.
En general, las leyes de conservación en los sistemas físicos corresponden a la existencia de simetrías, es decir, familias de transformaciones que no cambian la función de la energía del sistema. (Este hecho se conoce como el Teorema de Noether.) Por ejemplo, si la función de la energía del sistema no cambia bajo las traslaciones en cierta dirección, la proyección del momento cinético hacia esta dirección es constante. En general, la cantidad conservada puede considerarse como una "simetría infinitesimal" o, en otras palabras, como la derivada de una familia de simetrías.
El potencial gravitacional en un sistema de dos cuerpos es una función de la distancia del centro de masas, y, por lo tanto, es invariante bajo todas las rotaciones alrededor de él. La cantidad conservada que corresponde a esta simetría es el vector del momento angular $$\vec{L} = \vec{r} \times \vec{p},$$ donde $\vec{r}$ es el vector de la posición y $\vec{p} = m\, d\vec{r} /dt$ es el momento cinético. El vector $\vec{L}$ del momento angular y el vector de la posición $\vec{r}$ son perpendiculares; en otras palabras, el vector de la posición pertenece al plano perpendicular a $\vec{L}$. Como $\vec{L}$ es constante, esto significa que el movimiento de un planeta se desarrolla siempre dentro del mismo plano. El área que barre el vector de la posición en una unidad de tiempo es exactamente $L/m$ y, entonces, es constante; así obtenemos la segunda ley de Kepler.
La ley de la conservación del momento angular es válida en cualquier campo de fuerza central. En el caso del potenical gravitacional $-k/r$, existe una simetría adicional (la que suelen llamar "la simetría escondida"). La cantidad conservada que le corresponde es el vector de Runge-Lenz definido como $$\vec{A} = \vec{p}\times \vec{L} - mk\, \frac{\vec{r}}{r}.$$ Suponiendo que $A$ y $L$ son constantes, obtenemos que la órbita del planeta es una elipse (vean el recuadro del lado derecho). El hecho de que el Sol está en uno de los focos de la órbita es aproximado; sin embargo, notemos que el centro de masas del sistema Sol-Tierra está bajo la superfície del astro, a menos de 450 km de su centro.
Resulta algo difícil describir la simetría escondida explícitamente. No es una simetría del espacio tridimensional, sino una familia de transformaciones que involucran tanto las coordenadas como los momentos cinéticos. El procedimiento matemático que describe esta simetría es la regularización del problema de Kepler; la mejor introducción a este tema es el artículo de Milnor [Mi]J.Milnor, On the geometry of the Kepler problem, American Mathematical Monthly 90 (1983) 353-365.. Resulta que, junto con las rotaciones del espacio, las simetrías escondidas forman el grupo $SO(4)$ de rotaciones de un espacio euclidiano de la dimensión 4. Esta insólita aparición de un espacio cuatridimensional es algo misterioso; sin embargo, no nos queda otra que aceptar este fenómeno como un artefacto matemático del problema.
Como suele suceder, las elipses y las simetrías escondidas del movimiento planetario sólo existen en una primera aproximación. Por ejemplo, según la teoría especial de la relatividad, las órbitas en un sistema de dos cuerpos realmente no son cerradas. Sin embargo, el efecto más inmediato son las correcciones causadas por la gravitación de otros planetas. Estas correcciones fueron lo suficentemente grandes como para poder predecir la existencia de los planetas más allá de la órbita de Urano. Así, al observar la órbita de Urano se descubrió Neptuno y, a su vez, estudiando la órbita de Neptuno, se encontró Plutón.
De hecho, las perturbaciones a la órbita de la Tierra inducidas por otros planetas pueden ser lo suficientemente grandes como para haber preocupado, en su momento, a los astrónomos. Afortunandamente, según los cálculos de varios matemáticos y astrónomos, no tenemos nada que temer sobre una posible inestabilidad en el sistema solar (desgraciadamente, no hacen falta otros peligros). Sin embargo, todos estos cálculos usan métodos aproximados. Esto es inevitable, ya que el problema de tres o más cuerpos presenta comportamiento caótico (este hecho fue demostrado por Poincaré [Po]H.Poincaré, New methods in celestial mechanics. Traducido de la edición original francesa de 1892-1899. History of Modern Physics and Astronomy. 13. Bristol: American Institute of Physics, 1993.).
La característica principal del comportamiento caótico de un sistema de ecuaciones diferenciales (como lo son las ecuaciones de movimiento) es el hecho de que un cambio pequeño en las condiciones iniciales produce desviaciones exponencialmente grandes en las soluciones. Una consecuencia de ello es que las soluciones, aunque calculables en teoría (vean [Diacu] para una discusión detallada), se vuelven completamente impredecibles desde el punto de vista práctico; en particular, no existe ninguna fórmula general en términos de las integrales y funciones algebráicas que las describa. Vale la pena mencionar que la gran mayoría de sistemas físicos exhiben un comportamento caótico. Probablemente, el ejemplo más ilustrativo es el péndulo doble: después de observarlo en acción uno abandona cualquier esperanza de resolver sus ecuaciones de movimiento por medio de una fórmula.
La no existencia de una solución general al problema de tres cuerpos no impide a que existan soluciones particulares explícitas. Las soluciones periódicas son de interés especial. Euler observó que existen soluciones periodicas donde los tres cuerpos son colineales en cada momento. Lagrange encontró soluciones periodicas con la propiedad de que cada cuerpo traza una elipse y, en cada momento, los tres cuerpos forman un triángulo equilátero. Las soluciones de Euler y de Lagrange son muy relevantes en astronomía. Supongamos, por ejemplo, que uno de los tres cuerpos (digamos, un satélite) tiene masa despreciablemente pequeña comparada con los otros dos (digamos, la Tierra y la Luna), los cuales tienen órbitas circulares, y que todos los movimientos no salen de un plano fijo. En esta situación, el satélite puede ocupar una órbita circular permaneciendo en uno de los cinco puntos de Lagrange. Tres de estos puntos son colineales con la Tierra y la Luna, y la posición del satélite, en estos casos, sería inestable: cualquier empujón pequeño lo movería más y más lejos con el tiempo. Otros dos puntos de Lagrange son estables y corresponden al tercer vértice de un triángulo equilátero cuyos primeros dos vértices son la Tierra y la Luna. Claramente, hay dos triángulos con esta propiedad. Un punto de Lagrange sigue a la Luna en su movimiento alrededor de la Tierra con un retraso angular de 60 grados; el otro precede a la Luna con la misma distancia angular. Los puntos de Lagrange en el sistema Tierra-Luna se usan para los satélites geoestacionarios; también, se han enviado naves espaciales a los puntos de Lagrange del sistema Sol-Tierra. Planetas grandes como Jupiter están precedidos y seguidos en su viaje alrededor del Sol por miles de asteroides en sus puntos de Lagrange estables. Hay muchos más ejemplos naturales de sistemas de tres cuerpos de este tipo. Por supuesto, en todos estos casos, las trayectorias solamente se aproximan a la solución periódica exacta, dado que existen otras influencias gravitacionales.
Hace 20 años el problema de tres cuerpos vio un avance sorprendente. Usando cálculos numéricos, Cristopher Moore encontró una solución extraña al problema de tres cuerpos cuando las tres masas son idénticas [Moore]C.Moore, Braids in Classical Dynamics, Physical Review Letters 70 (1993) 3675-3679.. Los tres cuerpos siguen uno al otro por una misma órbita que tiene la forma de un ocho; el movimiento es similar al malabarismo con tres pelotas:

El descubrimiento de la solución en forma de ocho inspiró una búsqueda de soluciones similares para el problema de N cuerpos con N>3. Experimentos numéricos produjeron literalmente cientos de ejemplos de malabarismos graviacionales (llamados, hoy en día, coreografías, probablemente para evitar que la música celeste suene como una banda de circo). En cada una de estas soluciones coreográficas, los N cuerpos de masas iguales siguen uno al otro por la misma trayectoria. Los movimientos de los cuerpos son idénticos, salvo un retraso, el cual es el mismo para cada par de cuerpos consecutivos. Ejemplos de las coreografías se pueden encontrar en el recuadro al lado derecho de la página (para verlos en movimiento, visiten la página de James Montaldi).
Las soluciones coreográficas no son necesariamente planas. Uno puede obtener coreografías tridimensionales perturbando órbitas planas, pero también existen soluciones más interesantes. Por ejemplo, para cada sólido platónico existe una coreografía que tiene las simetrías de este sólido (los primeros ejemplos aparecieron en [DTWI.Davies, A.Truman, D.Williams, Classical periodic solutions of the equal-mass 2n-body problem, 2n-ion problem and the n-electron atom problem, Physics letters A, 99, no. 1, (1983) 15-18., HoG. Hoynant, Des orbites en forme de rosette aux orbites en forme de pelote, Sciences 99 no. 2 (1999) 3-8., CVA.Chenciner, A.Venturelli, Minima de l'intégrale d'action du Problème newtonien de 4 corps de masses égales dans R^3 : orbites "hip-hop", Celestial Mechanics, 77 (2000) 139-152.] y la lista completa, con una demostración matemática - en [FGN]G.Fusco, G.F.Gronchi, P.Negrini, Platonic polyhedra, topological constraints and periodic orbits of the classical N-body problem, Inventiones Mathematicae, 285 no. 2 (2011) 283-332.).
En general, las simetrías son de gran utilidad en el estudio de las órbitas coreográficas. Por ejemplo, Chenciner y Montgomery, para demostrar la existencia de la figura ocho, construyeron una doceava parte de la órbita y demostraron que este segmento se puede extender por simetría a una trayectoria cerrada (una exposición accesible de su demostración se puede encontrar en [Mont]R.Montgomery, A new solution to the three-Body problem, Notices of the American Mathematical Society 48 no. 5 (2001) 471-481.). Recientemente, las posibles simetrías de las coreografías planas se han clasificado en [MS]J.Montaldi, K.Steckles, Classification of symmetry groups for planar n-body choreographies, Forum of Mathematics, Sigma 1 (2013) e5 (55 páginas)..
Tomemos dos planos horizontales en el espacio, con $n$ puntos distintos marcados en cada plano. Supongamos que, a cada punto marcado en el plano superior, le corresponde un punto marcado en el plano inferior, exactamente debajo de él. Una trenza consiste de n caminos descendientes que conectan los puntos marcados en el plano superior con los puntos marcados del plano inferior, de tal suerte que ningunos dos de los caminos se intersectan. Dos trenzas son del mismo tipo topológico si una se puede deformar en la otra sin crear autointersecciones.
Hay varias razones para estudiar trenzas. Se usan en la teoría de nudos: cada nudo se puede obtener juntando los extremos de una trenza:
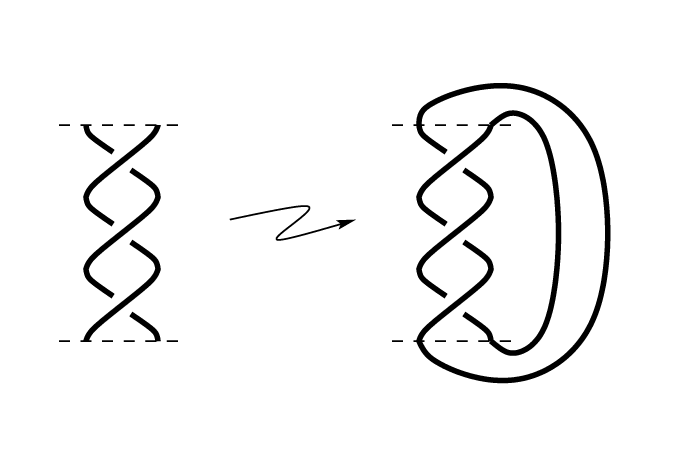
Otra propiedad de las trenzas es que se pueden multiplicar simplemente al colocar una trenza encima de la otra:
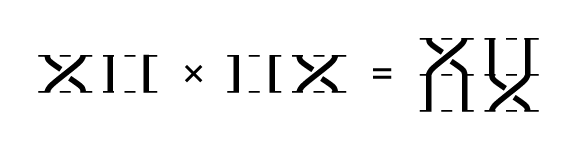
Si la coordenada vertical se concibe como el tiempo, una trenza puede considerarse como una trayectoria de movimiento simultaneo de $n$ puntos distintos en un plano. La pregunta que trataba de resolver Moore cuando llegó a descubrir la primera coreografía fue: ¿cuáles son los tipos topológicos de trenzas posibles como trayectorias en el problema de $n$ cuerpos? Se puede demostrar que, para un potencial de interacción de la forma $-k/r^d$ con $d>1$, cualquier tipo topológico de trenzas puede obtenerse como trayectoria. Sin embargo, para el caso $d=1$, es decir, para el potencial newtoniano en el espacio, casi no se sabe nada todavía.
Para buscar trayectorias del problema de $n$ cuerpos dentro de un tipo topológico de trenzas se usa el principio de la acción mínima. Este principio nos da una forma muy general para construir la mecánica newtoniana; según él, entre todos los movimientos imaginables de un sistema físico, el movimiento que es físicamente posible en realidad es el que minimiza la cantidad que se llama acción. En particular, dado un tipo topológico de trenzas, puede escogerse una trenza de este tipo arbitrariamente y ver cómo se comporta la acción del movimiento a lo largo de esta trenza bajo modificaciones pequeñas de las trayectorias de cada cuerpo. Así, deformando la trenza para minimizar la acción, se puede llegar a una trayectoria física.
El problema de minimizar la acción se puede simplificar si, en lugar de todos los caminos en el espacio de todas las posibles configuraciones de $n$ cuerpos, se consideran caminos en el llamado espacio de formas. Este último no es otra cosa que el espacio de todas las configuraciones de $n$ cuerpos consideradas ``salvo rotaciones y traslaciones''. Si el espacio de configuraciones de 3 cuerpos en el plano tiene dimensión 6, el espacio de formas correspondiente es tridimensional y más cómodo para los cálculos. Los detalles se pueden encontrar en el artículo de MontgomeryR.Montgomery, A new solution to the three-Body problem, Notices of the American Mathematical Society 48 no. 5 (2001) 471-481..
La probabilidad de descubrir una coreografía por medio de obsevaciones astronómicas es prácticamente nula. Hay varias razones para esto. Casi todas las soluciones coreográficas son inestables; la única coreografía donde se observa la estabilidad es la figura ocho de Moore. Además, a diferencia de las soluciones de Euler y Lagrange, todas las soluciones coreográficas involucran masas idénticas. La probablidad de encontrar tres estrellas cercanas de la misma masa es muy baja; aún más inverosimil sería verlas moverse en un baile a lo largo de la figura ocho. Se estima que, en todo el universo conocido, no ha de haber más de 100 sistemas estelares de este tipo [He]D.C.Heggie, A new outcome of binary-binary scattering, Monthly Notices of the Royal Astronomical Society, 318L, 61 (2000) L61-L63..
Sin embargo, existe un contexto donde uno suele encontrar masas idénticas: es el mundo microscópico. Aquí el problema de $n$ cuerpos aparece en un lugar inesperado. Tomemos un cilíndro superconductor y coloquémoslo en el campo magnético paralelo a su eje. En general, el campo magnético no puede penetrar un superconductor. La razón para ello es que, en ausencia de la resistencia eléctrica, aparecen unas corrientes cuyo campo magnético inducido cancela el campo exterior. Sin embargo, si el campo magnético es muy fuerte, las corrientes son demasiado grandes y la superconductividad se pierde; esto sucede a lo largo de unos filamentos que conectan las tapas del cilíndro.
Este efecto físico es bien conocido y tiene aplicaciones espectaculares, pero la descripción matemática de este fenómeno todavía no es completa. Un problema que se ha estudiado en [dPK]M.del Pino, M.Kowalczyk, Renormalized energy of interacting Ginzburg-Landau vortex filaments, Journal of the London Mathematical Society, II Series, 77, no. 3 (2008) 647-665. es la interacción de filamentos cercanos. Lo que sugieren los resultados de [dPK]M.del Pino, M.Kowalczyk, Renormalized energy of interacting Ginzburg-Landau vortex filaments, Journal of the London Mathematical Society, II Series, 77, no. 3 (2008) 647-665. es que los filamentos magnéticos pueden estar entrelazados. Más aún, ¡las trenzas que forman estos filamentos son gráficas de soluciones del problema de $n$ cuerpos idénticos en el potencial logarítmico! Lo anterior abre la posibilidad teórica de observar las coreografías en la naturaleza, aunque todavía no se sabe si el entrelazamiento de los filamentos magnéticos es un fenómeno real o solamente es una peculiaridad del modelo matemático.
[BB] J.Birman, T.Brendle, Braids: A Survey, arXiv:math/0409205 [math.GT].
[CM] A.Chenciner, R.Montgomery, A remarkable periodic solution of the three-body problem in the case of equal masses, Annals of Mathematics (2) 152, No.3 (2000) 881-901.
[CV] A.Chenciner, A.Venturelli, Minima de l'intégrale d'action du Problème newtonien de 4 corps de masses égales dans R^3 : orbites "hip-hop", Celestial Mechanics, 77 (2000) 139-152.
[DTW] I.Davies, A.Truman, D.Williams, Classical periodic solutions of the equal-mass 2n-body problem, 2n-ion problem and the n-electron atom problem, Physics Letters A, 99, no. 1, (1983) 15-18.
[dPK] M.del Pino, M.Kowalczyk, Renormalized energy of interacting Ginzburg-Landau vortex filaments, Journal of the London Mathematical Society, II Series, 77, no. 3 (2008) 647-665.
[Diacu] F.Diacu, The solution of the n-body problem, The Mathematical Intelligencer, 18 no. 3 (1996) 66-70.
[FGN] G.Fusco, G.F.Gronchi, P.Negrini, Platonic polyhedra, topological constraints and periodic orbits of the classical N-body problem, Inventiones Mathematicae, 285 no. 2 (2011) 283-332.
[He] D.C.Heggie, A new outcome of binary-binary scattering, Monthly Notices of the Royal Astronomical Society, 318L, 61 (2000) L61-L63.
[Ho] G. Hoynant, Des orbites en forme de rosette aux orbites en forme de pelote, Sciences 99 no. 2 (1999) 3-8.
[KT] C.Kassel, V.Turaev, Braid groups, Springer, New York, 2008.
[Mi] J.Milnor, On the geometry of the Kepler problem, American Mathematical Monthly 90 (1983) 353-365.
[Moore] C.Moore, Braids in Classical Dynamics, Physical Review Letters 70 (1993) 3675-3679.
[MS] J.Montaldi, K.Steckles, Classification of symmetry groups for planar n-body choreographies, Forum of Mathematics, Sigma 1 (2013) e5 (55 páginas).
[Mont] R.Montgomery, A new solution to the three-Body problem, Notices of the American Mathematical Society 48 no. 5 (2001) 471-481.
[Po] H.Poincaré, New methods in celestial mechanics. Traducido de la edición original francesa de 1892-1899. History of Modern Physics and Astronomy. 13. Bristol: American Institute of Physics, 1993.
