Nudos y Teoría Cuántica

En la vida diaria, una cuerda — tal como una agujeta — se emplea usualmente para asegurar algo o mantenerlo en su lugar. Cuando amarramos un nudo, el propósito es ayudar a la cuerda a realizar su trabajo. A menudo, terminamos con un complicado enredo con la cuerda, pero esto ocurre regularmente por error.

El término "nudo" como es usado por los matemáticos es solo una pequeña abstracción de esta experiencia. Un nudo, en el sentido matemático, es un lazo posiblemente enredado flotando libremente en el espacio ordinario. Así, los matemáticos estudian el enredo mismo. Un nudo típico en el sentido matemático se muestra en la Figura 1. Con un poco de suerte, esta figura nos recuerda algo que conocemos de la vida cotidiana. Puede ser bastante difícil darle sentido a un pedazo de cuerda enredada y decidir cuando ésta puede ser desenredada y si es así cómo. Es igualmente difícil decidir si dos enredos son equivalentes.

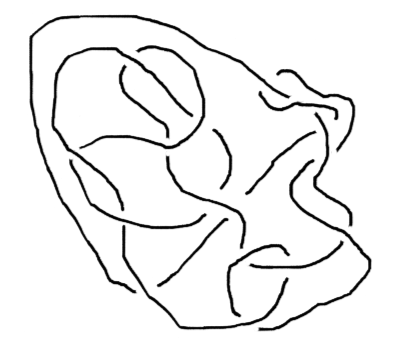
Tales preguntas podrían no escucharse como matemáticas, si uno está acostumbrado a pensar que las matemáticas tratan de sumar, restar, multiplicar y dividir. Pero de hecho, en el siglo veinte, los matemáticos desarrollaron una teoría bastante profunda de los nudos, con maneras sorprendentes de responder preguntas como cuándo un enredo dado puede ser desenredado.

Pero, aparte del hecho de que el tema es divertido ¿por qué estoy escribiendo sobre esto como un físico? Aun cuando los nudos son cosas que pueden existir en el espacio ordinario tridimensional, como físico solo estoy interesado en ellos debido a algo sorprendente que fue descubierto en las últimas tres décadas. Mucha de la teoría de nudos es mejor entendida en el marco de los desarrollos de la mecánica cuántica del siglo veinte y veintiuno. En otras palabras, lo que realmente me fascina no son los nudos en sí, sino las conexiones entre los nudos y la física cuántica.

El primer "polinomio de nudos" fue de hecho descubierto en 1923 por James W. Alexander. Alexander, originario de Princeton, posteriormente fue uno de los primeros profesores del Instituto para Estudio Avanzado (IAS) y pionero de la topología algebraica. Pero la historia como la contaré comienza con el polinomio de Jones, el cual fue descubierto por Vaughan F. R. Jones en 1983. El polinomio de Jones fue esencialmente una nueva forma de estudiar nudos. Su descubrimiento desencadenó una avalancha de nuevas sorpresas que continúan hasta nuestros días.

Aun cuando es muy moderno y cerca de la frontera de las matemáticas contemporáneas, el polinomio de Jones se puede describir de una forma más terrenal, tal que uno podría explicarlo en una clase de bachillerato sin tener que comprometer mucho. No hay muchos desarrollos de frontera en las matemáticas modernas sobre las que uno pueda hacer tal afirmación. Por ejemplo, nadie trataría de explicar la prueba de Andrew Wiles del último teorema de Fermat a estudiantes de bachillerato.

Para simplificar un poco (ver el recuadro del lado derecho de la página para mayores detalles), lo que Jones descubrió fue una forma de calcular un número para cada nudo. Vamos a llamar a nuestro nudo $K$, y escribiremos $J_K$ para el número que Jones calcula para este nudo. Hay una regla precisa que permite calcular $J_K$ para cualquier nudo. No importa lo complicado que $K$ pueda ser, uno puede calcular $J_K$ si se es suficientemente paciente.

Si $J_K$ no es igual a 1, entonces el nudo $K$ nunca puede ser desenredado. Por ejemplo, regresemos al nudo que se bosqueja en la Figura 1. Si usted pensara en cómo desamarrar ese nudo particular, seguramente no tendría éxito. Pero ¿cómo podría uno probar que es imposible? Jones dio una forma de cómo responder esta pregunta: calcule $J_K$ y si no es igual a 1, entonces el nudo nunca podrá ser desatado. El método de Jones para calcular $J_K$ fue muy inteligente, pero una vez encontrado, cualquier persona podría utilizarlo sin ninguna inteligencia particular, solo siguiendo las instrucciones.

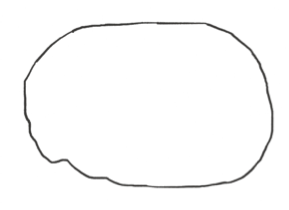
De hecho, hay una variedad sorprendente de formas para calcular $J_K$. Explicaré solo una de las más simples. Una regla importante se aplica al caso del nudo trivial, que es un lazo simple desenredado (Figura 2). Si $K$ no tiene ningún nudo entonces $J_K=1$.

Para todos los otros nudos, tenemos que jugar un poco. Para comenzar, escojamos tres números favoritos, por ejemplo 2, 3 y 10. Ahora vamos a hacer algo que puede parecer que hará la vida más complicada. En lugar de un solo nudo $K$ vamos a considerar tres nudos $K$, $K'$ y $K''$. Si los tres nudos que escogimos están relacionados de cierta manera, habrá una relación aritmética

Esta relación — o como los matemáticos la llaman, esta identidad — es tan poderosa que nos permite calcular los $J$.

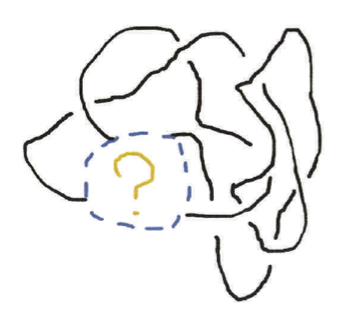
¿Cómo deben $K$, $K'$ y $K''$ estar relacionados para participar en tal identidad? En la Figura 3, he dibujado un nudo parcial. Es solo un nudo parcial porque hay una pieza que falta, indicada por el signo de interrogación. Hay muchas formas posibles de completar el nudo llenando la pieza que falta. En la Figura 4, he bosquejado tres de las formas más simples de hacer esto. Escogiendo una de estas tres formas obtenemos un nudo que llamaremos $K$, $K'$ o $K''$ respectivamente, y entonces, según se indicó previamente, declaramos que los números de Jones $J_K$, $J_{K'}$ y $J_{K''}$ cumplen la relación $2J_K+3J_{K'}+10J_{K''}=0.$

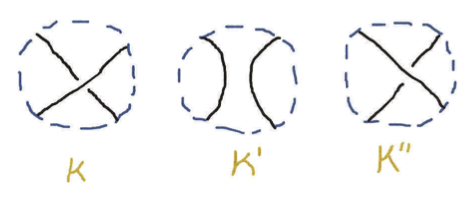
Resulta que esta es una relación muy poderosa que permite calcular $J_K$ para cualquier $K$. Los detalles de esto están explicados de una forma más completa en el recuadro del lado derecho.

La sorpresa aquí no es tanto que esta regla pueda ser usada para calcular $J_K$, sino que al hacer esto uno nunca llega a una contradicción. Uno podría anticipar una contradicción porque realmente hay muchas formas de usar las propiedades que he descrito para calcular $J_K$. Sin embargo, Jones y otros matemáticos mostraron en los años ochenta que nunca hay contradicción, siempre llega uno a la misma respuesta para $J_K$, sin importar cómo utiliza uno el procedimiento que acabo de describir (o alguno de los otros procedimientos relacionados que fueron descubiertos en ese periodo) para calcularlo.

Estas pruebas mostraron que las recetas para calcular $J_K$ eran correctas, pero dejaban una pregunta de "¿por qué?" Desafortunadamente, no es tan fácil explicar a alguien que no trabaja en matemáticas o física, o en un campo aledaño, la diferencia entre saber qué algo es verdad y saber porqué es verdad. Y, sin embargo, la belleza de las respuestas del "por qué" es gran parte de la razón por la que la gente hace matemáticas.

En este caso, mientras la gente trabajaba en el polinomio de Jones, descubrían más y más fórmulas notables, con menos y menos claridad sobre lo que ellas significaban. Pero había una pista. De hecho, había muchas pistas. Conforme el tema se desarrollaba, empezando con el trabajo original de Jones, este tuvo muchas conexiones con la física matemática ... desconcertantemente muchas. En todo caso, se encontraron demasiadas relaciones entre el polinomio de Jones y la física matemática. A veces es mejor tener una buena pista que ¡una docena de méritos dudosos!

Personalmente, fui influenciado durante este periodo por el trabajo de varios miembros del IAS, Erik Verlinde, Greg Moore y Nati Seiberg (Seiberg es ahora un profesor en la Escuela de Ciencias Naturales) y de los matemáticos japoneses Akihiro Tsuchiya y Yukihiro Kanie, y por las sugerencias de un anterior profesor del IAS, Michael Atiyah.

Resultó que la explicación del polinomio de Jones tiene que ver con la teoría cuántica. Necesito entonces explicar un poco de cómo la teoría cuántica difiere de la física previa al siglo veinte.

Una partícula clásica que viaja entre un punto y otro llega ahí en una órbita bien definida que obedece las leyes de Newton (Figura 5a). En contraste, una partícula cuántica puede seguir cualquiera de todas las trayectorias. Una trayectoria bastante típica puede ser absolutamente irregular (Figura 5b). Para la partícula cuántica debemos permitir todos los caminos posibles, con cualquier número de lazos y zigzags.

Un punto importante por enfatizar es que somos físicos relativistas, ya que la relatividad también fue inventada en el siglo veinte junto con la mecánica cuántica. Entonces cuando dibujo una trayectoria, ésta es realmente una trayectoria en el espacio-tiempo, no una trayectoria en el espacio.

La dimensión física del mundo real en el que vivimos es por lo tanto cuatro — tres dimensiones espaciales y una dimensión del tiempo. Pero para entender la teoría de nudos, al menos por el momento, vamos a imaginar un mundo de solo tres dimensiones espaciotemporales — dos dimensiones espaciales y una temporal.

En un mundo de tres dimensiones espaciotemporales, el camino de la partícula podría estar anudado. Para un ejemplo de un camino anudado, ver la Figura 6.

Un físico cuántico tiene que sumar los efectos de todos los posibles caminos por los que una partícula pueda alcanzar su destino. Cómo calcular tal suma es lo que los físicos aprendieron al construir la teoría cuántica y que es ahora el Modelo Estándar de la física de partículas.

En la mecánica cuántica, aunque cualquier camino es posible, si la partícula ha viajado por un camino particular $K$, entonces hay una "amplitud de probabilidad" para que ella llegue a su destino, y esta amplitud depende de $K$. La forma en que la amplitud depende de $K$ es muy importante - es la razón de que hay algún orden incluso en un universo cuántico. Todos los caminos son posibles, pero aquellos peculiares con muchos zigzags no son muy probables.

La amplitud mecánico cuántica que la partícula ha viajado en un camino $K$ está dada por algo llamado el operador de Wilson, $W_K$. Para nuestros propósitos, no necesitamos realmente saber cómo está definido. Todo lo que necesitamos saber es que es un ingrediente básico en la física cuántica; por ejemplo, los físicos lo usan para calcular la fuerza entre los cuarks.

La conexión entre el polinomio de Jones y la física cuántica resulta ser simple si consideramos un nudo $K$ como la órbita en el espacio tiempo de una partícula cargada, entonces el polinomio de Jones es el valor promedio del operador de Wilson. Entonces la fórmula cuántica para el polinomio de Jones es solo $J_K=\langle W_K\rangle$, donde el símbolo $\langle\ \rangle$ representa un proceso de promedio cuántico.

Cuando se realiza este programa, la versión de la teoría cuántica que es relevante usa algo llamado la función de Chern-Simons para campos de Norma. (Tanto Shiing-Shern Chern, quien fundó mucho de la geometría diferencial moderna, y James Simons, fueron miembros del IAS).

Esta historia como la he contado hasta ahora se remonta a mis primeros años en el Instituto. Pero en realidad hay un giro más actual para este cuento. Esta es la razón por la que me parece oportuno escribir sobre este tema ahora.

En la vida diaria, un nudo es un objeto físico que existe en el espacio, pero para interpretar el polinomio de Jones en términos de la teoría cuántica, tenemos que ver en cambio un nudo como un camino en un espacio tiempo de solo tres dimensiones. Esto es tal vez un punto de vista menos obvio sobre lo que un nudo significa.

Sin embargo, alrededor de 1990, cuando era miembro en el Instituto, Igor Frenkel empezó a desarrollar lo que él esperaba sería una nueva teoría matemática en la cual el nudo, de hecho, sería visto como un objeto físico, más que un camino en el espacio tiempo. La nueva teoría se supone que involucraría una versión más poderosa del polinomio de Jones.

Me gustaría decir que yo le di a Frenkel un consejo útil, pero todo lo que hice fue decirle que eso no funcionaría, porque la función de Chern-Simons es especial para tres dimensiones y no tiene un tipo correcto de extensión para cuatro dimensiones. De hecho, fue una objeción delicada en ese momento, y estoy todavía sorprendido que resultara estar equivocada.

De cualquier forma, Frenkel continuó desarrollando esta idea, entre otros, con su estudiante Mikhail Khovanov y un miembro del IAS, Louis Crane. Finalmente, alrededor del año 2000, Khovanov creó lo que hoy es conocida como homología de Khovanov — un refinamiento del polinomio de Jones en el que el nudo es un objeto físico en cuatro dimensiones espaciotemporales, más que el camino de una partícula en un espacio tiempo de solo tres dimensiones.

La homología de Khovanov es como el polinomio de Jones, en que una vez que fue inventado, puede ser calculada por un conjunto de reglas explícitas, aunque estas reglas son mucho más sofisticadas que aquéllas que son empleadas en el polinomio de Jones. Yo no creo que uno intentaría explicar la definición de la homología de Khovanov a estudiantes de bachillerato.

La homología de Khovanov ha tenido un alto grado de impacto en las matemáticas. Por ejemplo, fue tema principal en un programa especial en la escuela de matemáticas en el Instituto hace unos cuantos años.

No necesita uno física cuántica para definir la homología de Khovanov, aunque uno puede necesitar de la física cuántica para entender qué significa. De hecho, en 2004, los físicos Sergei Gukov, Albert Schwarz y Cumrun Vafa propusieron una interpretación cuántica de la homología de Khovanov, basada en un trabajo previo de Vafa con Hirosi Ooguri. (Estos físicos fueron todos antiguos miembros del IAS y/o estudiantes.) Su historia usó muchas ideas novedosas sobre campos cuánticos, cuerdas y todo eso.

Por bella y poderosa que es su historia, siempre sospeché que debería de haber un camino más directo, y dediqué el último año tratando de construir uno. Aunque en un sentido tuve éxito, no estoy seguro de poder decir que yo encontré una ruta más directa o solo una algo diferente [1]Edward Witten, Fivebranes and Knots, http://arxiv.org/abs/1101.3216.

La diferencia principal entre la homología de Khovanov y el polinomio de Jones es que el objetivo de la homología de Khovanov es más abstracto. Mientras que el polinomio de Jones de un nudo $K$ es un número $J_K$, la homología de Khovanov de $K$ es un "espacio de estados cuánticos" conocido como $H_K$. Si se piensa en un nudo como un objeto físico en un espacio tridimensional, entonces $H_K$ es el espacio de sus posibles estados cuánticos.

Como la homología de Khovanov está dada en un espacio tiempo de cuatro dimensiones, más que de tres, ésta involucra ideas que son más cercanas a la física real de partículas que aquéllas relacionadas al entendimiento del polinomio de Jones.

Una idea importante es la simetría entre los campos eléctrico y magnético. Esto es llamado dualidad electromagnética, y fue iniciada en los años setenta por Peter Goddard (actual director del Instituto), Jean Nuyts, y David Olive (todos antiguos miembros del IAS). Desde mediados de los años noventa, ha sido una de las principales herramientas en estudios de campos cuánticos y cuerdas, en el Instituto y en otros lados. El uso de la dualidad electromagnética es de hecho crucial para evitar el obstáculo que me había convencido veinte años antes, que la idea de Igor Frenkel no funcionaría.

Otra faceta de la teoría de cuerdas también resulta ser importante: las dimensiones extras. Aun cuando lo que queremos se supone que es una teoría en cuatro dimensiones espaciotemporales, resultó que entenderla propiamente, involucra relacionarla con teorías en cinco o seis dimensiones.

La mayor sorpresa de todas es que aun cuando pueda ser definida por una receta explícita sin referencia a la física cuántica — y así es como fue descubierta — la homología de Khovanov se puede entender, posiblemente mucho mejor, usando las más modernas herramientas de la teoría cuántica de campos y de la teoría de cuerdas. Probablemente la historia completa involucra ideas físicas que nosotros no entendemos completamente, incluso ahora.

Referencia

[1] Edward Witten, Fivebranes and Knots, http://arxiv.org/abs/1101.3216