1. Miremos una de las más recientes esculturas de Sebastián:

Cuántica: simetría 5. Bronce patinado. 2013. $22\times 38.5 \times 23.5$ cm.

Desde luego que una escultura es un objeto tridimensional, por lo que se necesitan varias imágenes para poderla representar en una hoja de papel. Seleccionemos una de ellas:

La mayor parte de las personas encontrará que esta imagen es bella y agradable a la vista. La forma de sus curvas posee una belleza natural y una estructura matemática. En este ensayo, nos gustaría centrarnos en la relación entre las dimensiones estéticas de ambos quehaceres humanos: las matemáticas y la escultura.

2. En la mente de un matemático, las palabras belleza y matemáticas están íntimamente relacionadas; en palabras del experto en teoría de números británico G. H. Hardy:

Los patrones del matemático, como los del pintor o los del poeta, deben ser bellos; las ideas, al igual que los colores o las palabras, deben conjuntarse de una manera armoniosa. La belleza es la primera prueba a superar: en el mundo no hay un lugar permanente para las matemáticas feas [1]G. H. Hardy, A Mathematician's Apology, Cambridge [UK], The University Press, 1940..

La belleza parece trascender el arte específico que la encarna; Bertrand Russell, por ejemplo, compara la belleza de las matemáticas con la belleza de la escultura:

Las matemáticas, si se miran correctamente, no sólo poseen la verdad, sino también una belleza suprema — una belleza fría y austera, como la de la escultura, pero que no apela a ninguna parte de nuestra más débil naturaleza... [una belleza] de sublime pureza y capaz de alcanzar la severa perfección que sólo puede mostrar el mejor arte. En las matemáticas encontramos el verdadero espíritu del deleite, la exaltación, la sensación de ser algo más que sólo hombres, y ésta es la forma de medir la más alta excelencia.... [2]Bertrand Russell, The Study of Mathematics, Philosophical Essays, London/New York, Longmans/Green, 1910, pp. 73-74..

Por lo tanto, para nosotros la belleza es el concepto unificador que ofrece un puente entre el arte y las matemáticas. Ahora debemos detenernos un momento en el origen común del arte, las matemáticas y la belleza: la evolución darwiniana.

Consideremos dos rostros bellos: La mayor parte de la gente (aunque no toda) encontrará que el primer rostro es mucho más bello y agradable. Podemos adivinar que la mayoría de los chimpancés no estarían de acuerdo, y para ellos esto podría ser cuestión de vida o muerte. Para los humanos, parece plausible colocar el hecho de que la primera cara nos parezca más bella que la segunda (más placentera a la vista), en una adaptación que proporciona cierta ventaja al observador (un aumento en las probabilidades de pasar los genes propios a la siguiente generación). A partir de esta consideración, podríamos vernos tentados a concluir que lo bello es simplemente lo que le proporciona al observador una ventaja evolutiva: una especie de sensor de recompensas evolutivas convenientes a nivel visual o auditivo.

Denis Dutton ha desarrollado en forma exhaustiva este punto de vista, tanto en escritos como en video; un ejemplo de ello es su TED talk A Darwinian Theory of Beauty:

No me cabe la menor duda de que la experiencia de la belleza, con su intensidad emocional y placer, pertenece a nuestra evolucionada psicología humana. La experiencia de la belleza es uno de los componentes de una amplia serie de adaptaciones darwinianas. La belleza es un efecto adaptativo que extendemos e intensificamos para la creación y el disfrute del arte y del entretenimiento [3]Denis Dutton, A Darwinian Theory of Beauty, archivo en video, (2010, noviembre), tomado de: www.ted.com/talks/denis_dutton_a_darwinian_theory _of_beauty.html.

Sin embargo, esta no puede ser toda la historia.

3. Observemos algo muy curioso. Tanto el rostro del chimpancé como el rostro de la mujer, poseen una evidente simetría: en efecto, si trazamos una línea vertical justo a la mitad de la nariz, veremos que estas caras son esencialmente simétricas en relación con dicha línea. Existen de hecho investigaciones que sugieren que entre más simétricos sean los rostros humanos, más bellos los considerará la mayoría de la gente [4] Karl Grammer y Randy Thornhill, Human (Homo sapiens) Facial Attractiveness and Sexual Selection: The Role of Symmetry and Averageness, Journal of Comparative Psychology 108, no. 3 (1994): 233–242.. No es una coincidencia que la simetría facial también se relacione con la salud [5]5. B. C. Jones, A. C. Little, I. S. Penton-Voak, B. P. Tiddeman, D. M. Burt y D. I. Perrett, Facial Symmetry and Judgements of Apparent Health Support for a “Good Genes” Explanation of the Attractiveness-Symmetry Relationship, Evolution and Human Behavior 22, no. 6 (2001): 417–429..

Por lo pronto, entonces, hemos encontrado la siguiente cadena reduccionista:

Simetría → Salud → Belleza

Podríamos también argumentar que esto forma parte de una cadena reduccionista más larga:

Matemáticas → Física → Química → Biología → Simetría → Salud → Belleza

Evidentemente, aquí estamos simplificando demasiado la situación; sin embargo, podemos decir lo siguiente: a través de esta cadena reduccionista, de alguna manera las matemáticas avanzan sigilosamente hasta brindar la fuente de una parte de la belleza de estos rostros (una de las muchas fuentes posibles, ya que, a priori, la idea precedente no podría explicar cabalmente por qué preferimos el primer rostro).

Aquí un objetor podría argumentar que los chimpancés y los humanos son demasiado cercanos, en términos evolutivos; pero podríamos responder a esta objeción con una imagen llena de simetría:

Si consideramos la salud y el cuerpo biológico funcional como problemas a resolver — porque “la biología es ingeniería”, en palabras de Dan Dennett [6]Daniel C. Dennett, Darwin's Dangerous Idea: Evolution and the Meanings of Life, New York, Simon and Schuster, 1996. —, entonces el campo de las posibles soluciones se verá drásticamente restringido por las leyes de la naturaleza; si decidimos creer que muchas de las leyes de la naturaleza son de tipo matemático, entonces las estructuras de las matemáticas (como la simetría) tendrían mucho que ver con por lo menos una parte de lo que encontramos bello.

4. Pero, ¿cómo es posible que las leyes de la física, la química o la biología tengan una naturaleza matemática? ¿Acaso las matemáticas no son simplemente una invención humana? ¿No son una enorme tautología carente de contenido interno? ¿Es razonable esperar que la naturaleza se comporte de acuerdo con las leyes del ajedrez?

El que las leyes de la física sean matemáticas, parece ser algo aceptado y a la vez muy extraño. Tan es así, que Eugene Wigner escribió uno de los ensayos más famosos en la historia de la filosofía de la ciencia enfrentando esta incógnita. En su ensayo concluye lo siguiente:

El milagro de la validez del lenguaje de las matemáticas para la formulación de las leyes de la física, es un regalo maravilloso que ni entendemos ni merecemos. Deberíamos estar agradecidos por ello y confiar en que seguirá siendo válido en la investigación futura y se extenderá, para bien o para mal, hacia muchas ramas del aprendizaje, independientemente de si esto nos produce placer o perplejidad. [7]Eugene P. Wigner, The Unreasonable Effectiveness of Mathematics in the Natural Sciences, Communications on Pure and Applied Mathematics 13, no.1 (1960): 1–14.

En su ensayo, Wigner se muestra particularmente desconcertado por la naturaleza tan abstracta de la teoría cuántica, y más adelante tendremos que volver a este importante punto.

Los matemáticos somos, aunque en diferente medida, casi todos Platonianos; creemos que los objetos matemáticos existen independientemente de los seres humanos y de sus cerebros. Pensamos que las matemáticas (buenas y bellas) se descubren, no se inventan. En las matemáticas, hablamos más bien de descubrimientos y no de inventos.

En distintos momentos de sus vidas, los matemáticos se preguntan sobre la naturaleza de las matemáticas y sus objetos. Bertrand Russell vuelve en forma recurrente a la cuestión del realismo y del platonismo de las matemáticas:

Las matemáticas nos conducen más allá de lo humano, al territorio de la necesidad absoluta al cual debe conformarse no sólo el mundo real, sino cualquier mundo posible; [...]

Las matemáticas no sólo son independientes de nosotros y de nuestros pensamientos, sino que en el otro sentido, también nosotros y todo el universo de las cosas existentes independientes de las matemáticas [2]Bertrand Russell, The Study of Mathematics, pp. 73–74..

Veamos ahora una larga cita de un libro de Roger Penrose:

Hay algo importante que se gana cuando se considera que las estructuras matemáticas poseen una realidad propia, ya que nuestras mentes individuales son sumamente imprecisas, poco confiables e inconstantes en sus juicios. La precisión, la confiabilidad y la consistencia que requieren nuestras teorías científicas, exigen algo que va más allá de cualquiera de nuestras (poco confiables) mentes individuales. En las matemáticas encontramos una solidez mucho mayor respecto de la que podríamos hallar en cualquier mente específica. ¿Acaso esto no apunta hacia algo fuera de nosotros mismos, hacia una realidad que reside más allá de lo que cada individuo puede lograr? ...

Ciertamente las matemáticas, en sí, parecen tener una solidez que va mucho más allá de lo que cualquier matemático individual es capaz de percibir. Los que trabajan en este ámbito, ya sea que se dediquen en forma activa a la investigación matemática o que simplemente utilicen los resultados obtenidos por otros, por lo general se sienten meros exploradores en un mundo que se encuentra más allá de ellos mismos — un mundo que posee una objetividad que trasciende la simple opinión, ya sea que dicha opinión sea propia o haya sido vislumbrada por otros, sin importar cuan expertos estos otros pudieran ser...

Déjenme ilustrar este asunto tomando un famoso ejemplo de una verdad matemática y relacionándolo con la cuestión de la “objetividad”. En 1637, Pierre de Fermat presentó su famoso postulado, conocido como “el Último Teorema de Fermat”... La aseveración matemática de Fermat no se confirmó sino hasta 350 años después, no obstante los convenidos esfuerzos de numerosos matemáticos sobresalientes. Finalmente, en 1995 se publicó la demostración ...

¿Debemos considerar que el postulado de Fermat siempre fue cierto, desde mucho antes de que Fermat efectivamente lo expusiera, o debemos pensar que su validez es una cuestión puramente cultural, dependiente de cualesquiera que fueran los estándares subjetivos de la comunidad humana de los matemáticos? Supongamos que la validez del postulado de Fermat fuera, de hecho, una cuestión subjetiva. Entonces, no sería absurdo que a otro matemático X se le hubiera ocurrido un ejemplo real y específico, contrario a la aseveración de Fermat, siempre y cuando el matemático X lo hubiese presentado antes del 1995...

Yo creo que prácticamente todos los matemáticos, sin importar la postura que profesen en cuanto al “platonismo”, considerarían que esta posibilidad es evidentemente absurda [8]Roger Penrose and N. David Mermin, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, American Journal of Physics 58 (1990): 1214..

5. Hagamos una aseveración: desde el punto de vista estético, la belleza de las esculturas de Sebastián (Enrique Carbajal González, 1947) es más cercana a la belleza directa de las matemáticas que a la belleza, por decir algo, de las esculturas de Mathias Goeritz:

Al contemplar las Cuánticas de Sebastián, uno puede imaginar en forma intuitiva su simetría oculta (el origen de su equilibrio), así como su esencia geométrica; su naturaleza platónica nos recuerda lo que dice Brancusi sobre la simplicidad como fuente de la belleza escultural:

En el arte, la simplicidad no es un fin. Llegamos a ella a pesar de nosotros mismos, cuando nos acercamos a la realidad de las cosas [9]Catalogue of Brancusi Exhibition, New York, Wildenstein Gallery, 1926..

Lo que es real, no es la forma externa, sino la esencia de las cosas. Partiendo de esta verdad, es imposible que alguien pueda expresar algo esencialmente real a través de la imitación de su superficie externa [10]Catalogue of Brancusi Exhibition, New York, Brummer Gallery, 1926..

Yo nunca trato de realizar lo que se llamaría una forma pura o abstracta. La pureza, la simplicidad, nunca están en mi mente; la única finalidad es la de llegar al verdadero sentido de las cosas [11]Constantin Brancusi quoted by Dorothy Dudley, Brancusi, Dial 82 (1927): 126..

No es exagerado decir que las palabras simplicidad, pureza y abstracta en los pensamientos de Brancusi, corresponden a nuestro uso de las palabras platónico y matemático.

En las Cuánticas de Sebastián, percibimos cómo el concepto matemático de la simetría comienza a revelarnos al artista: Sebastián nunca ha negado de manera explícita el origen geométrico de su obra. Sus esculturas más recientes (Cuánticas, 2013) son producto de una investigación lúdica y profunda de la naturaleza del espacio y de sus recombinaciones formales. Las matemáticas serán nuestro intérprete en los misterios estéticos que éstas plantean. Analizaremos la pregunta de si son objetos platónicos, o sea residentes de buena fe en el reino platónico de las matemáticas.

Una vez más, recurrimos a Penrose:

La existencia platónica, como yo la veo, se refiere a la existencia de un estándar objetivo externo que no depende de nuestras opiniones individuales, ni de nuestra particular cultura. Esta “existencia” también podría referirse a algo distinto que las matemáticas, como la moralidad o la estética, pero lo que aquí nos interesa es la objetividad matemática, que parece ser una cuestión mucho más clara...

Platón mismo habría insistido en que hay otros dos ideales absolutos fundamentales, que son el de la Belleza y el de la Bondad. No estoy en lo absoluto en contra de aceptar la existencia de dichos ideales y de permitir que el mundo platónico se extienda para incluir absolutos de esta naturaleza [8]Penrose and Mermin, The Emperor's New Mind, p. 1214..

Tanto los artistas como los científicos, a menudo hablan de un rayo de inspiración que a veces cae en el momento mismo de la creatividad. Andrew Wiles, al describir su experiencia de haber descubierto la demostración del Último Teorema de Fermat, dice:

Quizás la mejor manera de describir mi experiencia al hacer matemáticas, es comparándola con un viaje a través de una oscura mansión inexplorada. Cuando uno entra a la primera habitación de la mansión, uno está en completa oscuridad. Se avanza a tropezones, golpeando contra los muebles, pero gradualmente uno aprende dónde se encuentra cada mueble. Finalmente, después de alrededor de seis meses, uno encuentra el interruptor de la luz, lo enciende y de repente todo se ilumina. Se puede ver exactamente dónde se ha estado. Luego uno se dirige a la siguiente habitación y se pasa otros seis meses en la oscuridad. Por lo tanto, todos estos hallazgos, que a veces sólo son momentáneos y otras veces duran un día o dos, son una culminación que únicamente puede existir después de muchos meses de haber tropezado en la oscuridad que los precedió [12]William Byers, How Mathematicians Think: Using Ambiguity, Contradiction, and Paradox to Create Mathematics, Princeton, Princeton University Press, 2010..

Tropezamos en la oscuridad por muchos meses o años, hasta que finalmente las musas se apiadan de nosotros y nos cae el rayo; aunque quizás no se trate de las musas, sino que por fin hemos avanzado por los caminos correctos de la realidad platónica para llegar a nuestro destino.

Sebastián también debe haber dado tropezones en la oscuridad, antes de, como veremos, poder jugar, recombinar y transgredir parcialmente la simetría que yace en los objetos y las formas del espacio y de la geometría, para llegar finalmente a su destino: la belleza de sus esculturas (más revelada que inventada); estas esculturas se muestran matemáticas y platónicas ante nuestra mirada.

6. Tomemos una de las Cuánticas y comencemos por un círculo:

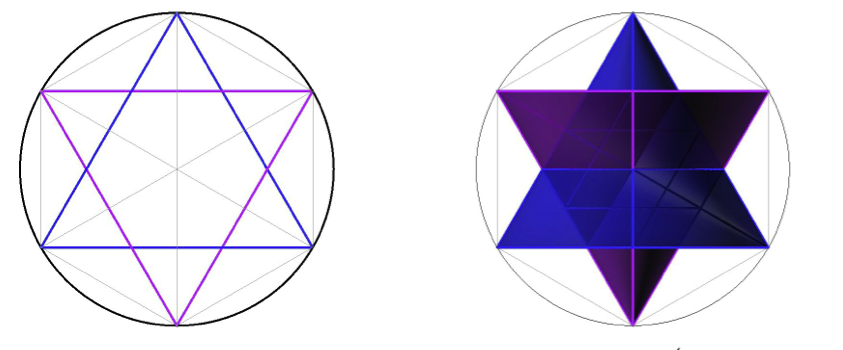
Sebastián comienza con un círculo que posee una simetría total y continua; luego, él rompe esta simetría para producir una simetría hexagonal. Posteriormente, gira la imagen a lo largo de su eje vertical, pasando a través del centro del círculo: por lo pronto, no son más que dos conos abrazados.

Sin embargo, observemos que si giramos el círculo (que contiene a los triángulos), a lo largo del mismo eje vertical de antes, obtenemos una esfera; imaginemos que se trata de una esfera de cristal; podremos ver, en su interior, los conos obtenidos como superficies de rotación. El nombre de esta exhibición es Esferas Cuánticas, ya que la mayor parte de las esculturas Cuánticas tienen su origen justamente en la esfera: la superficie matemática más simple y totalmente simétrica.

Aquí es donde ocurre la acción sorpresa: la recombinación. Rebanamos la imagen verticalmente, como rebanaríamos una naranja, pasando a través del plano que contiene al círculo original: obtenemos dos piezas idénticas, con una estrella de seis puntas sobre el plano rebanado y dos medios conos adheridos a cada una de las estrellas. Pero como las estrellas tienen una simetría que consiste en la rotación de un ángulo de 360/6 = 60 grados respecto del centro del círculo, simplemente giramos una mitad del sólido a 60 grados y luego pegamos de nuevo ambas mitades, después de haber girado una de ellas.

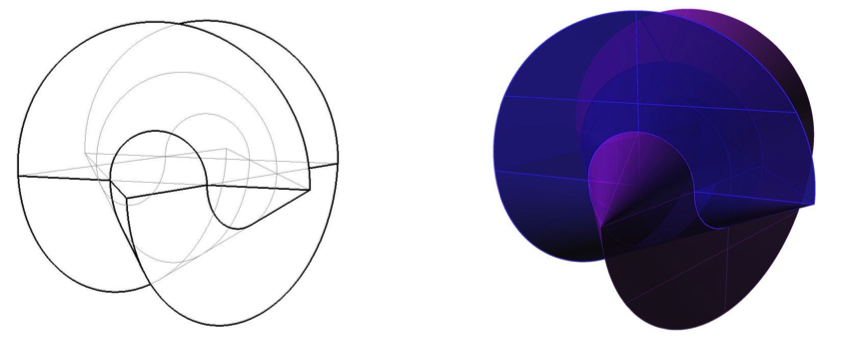
El volumen resultante es una de las Cuánticas de Sebastián.

Ahora veamos el proceso que se da con una simetría de orden cinco de 360/5 = 72 grados.

Esta pieza luce así, si la vemos del otro lado:

De hecho, usaremos dos piezas idénticas:

Si estas piezas se volvieran a pegar una con otra, se verían así:

Pero aquí, Sebastián decide efectuar una de sus recombinaciones: separamos las mitades y giramos una de ellas en un ángulo de 72 grados con respecto a la otra:

Ahora, simplemente volvemos a unir las mitades, después de haber efectuado la rotación:

Visto desde otro ángulo, quedaría así:

Finalmente, abandonando el universo esférico que le dio origen a la pieza, podemos prolongar uno de los ejes por un factor de, digamos, 1.5; es decir, multiplicamos toda la imagen por la matriz:

$$M=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1.5 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$

Esto rompe parte de la simetría y le da a la escultura un aire más enigmático:

Aquí vemos una de las más simples y bellas Cuánticas de Sebastián.

7. Las Cuánticas de Sebastián están hechas de espacio, simetría, simplicidad, geometría y belleza. Esta belleza sólo es aumentada por las transgresiones parciales de la simetría pura a las que las piezas son sometidas por el artista.

En su magistral libro sobre la simetría, Hermann Weyl [13]Hermann Weyl, Symmetry, Princeton, Princeton University Press, 1952; Princeton Science Library reprint (1989). señala que las simetrías parciales a veces son más placenteras, desde el punto de vista estético, que las simetrías matemáticas exactas. Él llama esta noción más general de la simetría Ausgewogenheit, y es una noción muy útil para nosotros. Weyl cita a Dagobert Frey (“Sobre el problema de la simetría en el arte”):

[La simetría] significa reposo y ataduras; la asimetría, movimiento y soltura; la primera, orden y ley; la segunda, arbitrariedad y accidente; la una, rigidez formal y restricción, mientras que la otra, juego de vida y libertad [14]Dagobert Frey, Zum Problem der Symmetrie in der bildenen Kunst, Studium Generale 2 (1949): 276..

Esto nos recuerda lo que ocurre cuando escuchamos variaciones sobre un tema musical: los cambios en la estructura, percibidos por el cerebro humano, producen una respuesta placentera una vez que se comprenden como parte de una estructura oculta o inesperada. Hay muchos ejemplos similares: cuando una trama repentinamente se torna sorpresiva en una novela de misterio o, lo que es quizás más arquetípico, el remate de un buen chiste.

Hurley, Dennett, y Adams proponen una perspectiva darwiniana para esta cuestión [15]Matthew M. Hurley, Daniel Clement Dennett y Reginald B. Adams, Inside Jokes: Using Humor to Reverse-Engineer the Mind, Cambridge (MA), MIT Press, 2011.. Ellos argumentan que es razonable sospechar que la acción de descifrar algo le cuesta trabajo al cerebro, y el éxito en este desciframiento (por ejemplo, de la simetría parcial) produce una respuesta satisfactoria con ventajas evolutivas: el placer estético supremo que nos brinda el haber comprendido las simetrías ocultas de las esculturas.

Y aquí es donde encaja la psicología de las matemáticas: el momento exacto del descubrimiento (en el que encontramos el interruptor del que hablaba Wiles), produce un intenso placer estético; el hallazgo de la elusiva demostracónn del teorema como épica acción de desciframiento, no es tan diferente a la acción creativa de la escultura de lo que podríamos inicialmente estar inclinados a pensar.

8. Así pues, el cerebro tiende a buscar la simplicidad en medio de la bruma de los detalles. En palabras de Weyl:

...Generalicemos gradualmente este concepto [de la simetría], ... quedándonos primero dentro de los límites de la geometría, pero luego yendo más allá de estos límite, a través del proceso de la abstracción matemática y siguiendo el camino que finalmente nos lleva a una idea matemática de gran generalidad, la idea platónica que yace detrás de todas las apariencias y aplicaciones especiales de la simetría.... Puede desaparecer gran parte de su atractivo emocional, pero posee un poder unificador igual o incluso mayor en el reino del pensamiento, y es exacta y no vaga.

Percibimos la encarnación matemática de la simetría como algo que posee una extraordinaria belleza y un gran atractivo emocional: el concepto de grupo.

Veamos ahora la definición matemática de un grupo:

Denominamos grupo a un conjunto G de transformaciones (acompañado por una operación o ley de combinación) que cumple con los siguientes axiomas:

1. Hay una ley de combinación que se asocia a todo par de elementos del conjunto $G$ $(x, y)$ tomados en ese orden; el elemento $z$, también perteneciente al conjunto $G$, es su combinación. Esta correspondencia se representa de la siguiente manera: $x*y = z$.
2. En todo elemento $x, y$ y $z$ del conjunto $G$, la ley de combinación es asociativa, es decir: $$(x * y) * z = x * (y * z).$$
3. En el conjunto $G$ también hay un elemento $e$, que hace que $$x * e = e * x = x$$ para cualquier elemento $x$ del conjunto $G$. Este elemento es único, por lo que se le conoce como elemento identidad.
4. Todo elemento $x$ del conjunto $G$ posee un elemento inverso $y$, perteneciente al mismo conjunto $G$; de manera que: $$ x * y = y * x = e.$$

No resulta muy emocionante al principio, pero aun así, Richard Borcherds, un experto en teoría de grupos, se ve impulsado a decir:

Los axiomas de un grupo son breves y naturales... Sin embargo, detrás de estos axiomas, de alguna manera se esconde el grupo simple [conocido como] Monstruo, un objeto matemático cuya existencia al parecer depende de numerosas coincidencias bizarras. Los axiomas de los grupos no ofrecen pistas evidentes sobre la existencia de algo así [16]M. R. Cook, R. C. Gunning, and B. Fradd, Mathematicians: An Outer View of the Inner World, Princeton, Princeton University Press, 2009, p. 24.

Esta definición tan breve y trascendental encierra una extraordinaria simplicidad y una gran densidad de información. Los grupos nacieron en el humilde reino de las ecuaciones algebraicas y hoy constituyen una parte fundamental del modelo estándar, una teoría cuántica de campo que explica en forma impresionantemente detallada todas las fuerzas de la naturaleza, exceptuando a la gravedad.

9. Sorprendentemente, los grupos no iniciaron su infección memética [17]Un meme (o mem) es una unidad de transmisión cultural humana análoga al gen. Véase Richard Dawkins, The Selfish Gene, New York, Oxford University Press, 1976. de la mente humana en el ámbito de la geometría, sino más bien en el campo de las ecuaciones algebraicas.

La teoría de grupos nació en la extraordinaria y asombrosa obra de Evariste Galois.

En la mente de Galois, los grupos se originaron como conjuntos de permutaciones en las raíces de un polinomio. Logró demostrar que la ecuación algebraica de quinto grado general no se podía resolver mediante radicales.

Galois murió en un duelo, el 30 de mayo de 1832, a los veinte años de edad. La noche anterior al duelo, Galois estaba convencido de su inminente muerte y se quedó despierto toda la noche para elaborar su testamento matemático, una monumental carta a Auguste Chevalier en la que esbozaba sus ideas, así como otras cartas a sus amigos. Citando de nuevo a Hermann Weyl (1952):

Esta carta, si se considera la originalidad y la profundidad de las ideas que contiene, es quizás el documento escrito más valioso de toda la literatura de la humanidad [18]Ivor Grattan-Guinness, ed. History and Philosophy of the Mathematical Sciences vol. 1, Baltimore, Johns Hopkins University Press, 2003..

10. Las ecuaciones son álgebra, mientras que la geometría estudia la estructura del espacio. Fue una gran sorpresa para los matemáticos darse lentamente cuenta de que la geometría y el álgebra son dos caras de una misma moneda. El campo de las matemáticas en el cual se produce este entendimiento se denomina geometría algebraica. Los conceptos básicos de la geometría algebraica se estudian incluso desde el bachillerato. A una figura geométrica elemental, se le acopla una ecuación algebraica.

11. En la geometría, los grupos son fundamentales porque encarnan el concepto de simetría.

Ilustremos ahora el más elemental de los grupos que no son triviales: el que se obtiene en el reflejo de un espejo, el grupo cíclico de orden 2.

H. S. M. Coxeter, uno de los más grandes geómetras del siglo XX, escribe lo siguiente:

Cuando un objeto es colocado frente a un espejo común, se ven dos cosas: el objeto y su imagen. Si Alicia pudiera llevarnos al otro lado del espejo, seguiríamos viendo las mismas dos cosas, porque la imagen de la imagen sería el objeto original. En otras palabras, un reflejo individual $R$ genera un grupo de orden 2 cuyas operaciones son $I$ y $R$. No hay ulteriores operaciones, ya que $R^2=I$ y por consiguiente $R^{-1}= R$. En vez de usar un espejo plano en el espacio, podríamos emplear un espejo lineal en un plano, o un espejo de punto sobre una línea. Un punto divide a una línea en dos medias líneas o rayos, y sirve como espejo para reflejar un rayo en el otro [19]H. S. M. Coxeter, Regular Polytopes, New York, Dover Publications, third edition, 1973, cf. Lewis Carroll, Through the Looking-Glass, and What Alice Found There, London, Macmillan and Company, 1871 [postdated on title page to 1872]..

En nuestro lenguaje algebraico, lo anterior se traduce como la relación:

$$\rho^2=1.$$

Consideremos otros ejemplos provenientes de la geometría. Para ello, debemos recordar que cuando estudiamos matemáticas en la escuela, nos enseñaron que las ecuaciones y las figuras sobre un plano están íntimamente relacionadas entre sí:

$$y=3x+4$$

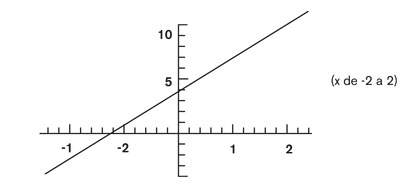
La imagen de arriba, una línea recta, corresponde a una ecuación lineal.

$$x^2+y^2=9$$

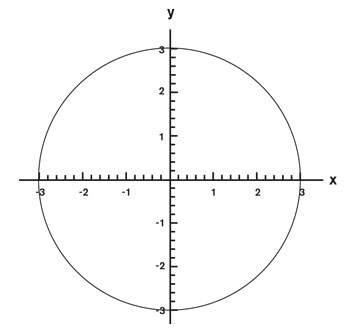
La más simétrica de las figuras sobre un plano es el círculo, y corresponde a un polinomio cuadrático. El círculo $S$ es el conjunto de soluciones para esta ecuación.

El grupo de simetrías del círculo, puede representarse como un conjunto de matrices de 2x2:

$$ G= \left\{ \begin{bmatrix} \pm \cos\theta & \mp\mathrm{sen}\,\theta \\ \pm\mathrm{sen}\,\theta & \pm\cos\theta \end{bmatrix} : 0\leq \theta \leq 2\pi \right\}$$

El conjunto de soluciones $S$ (o sea el círculo), hace que al tomar cualquier punto $p=(x,y)$ en el conjunto $S$ y cualquier elemento $g$ en el grupo $G$, obtengamos:

$$ \begin{bmatrix} \pm \cos\theta & \mp\mathrm{sen}\,\theta \\ \pm\mathrm{sen}\,\theta & \pm\cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \in S, \forall\ 0\leq \theta \leq 2\pi$$

O sea que $g(p)$ también satisface la ecuación cuadrática planteada, y este hecho es una simple consecuencia de las identidades trigonométricas estándar.

Los físicos y los matemáticos por lo general se refieren al grupo $G$ de este ejemplo como $O(2)$.

Ésta es la manera en la que generalmente se relacionan los grupos y la simetría, casi siempre pasando a través de grupos de matrices.

12. Con frecuencia no es necesario escribir las matrices, como lo hicimos en el ejemplo anterior. Consideremos una estrella de seis puntas inscrita dentro de un hexágono y numeremos sus vértices con los dígitos 1, 2, 3, 4, 5, 6.

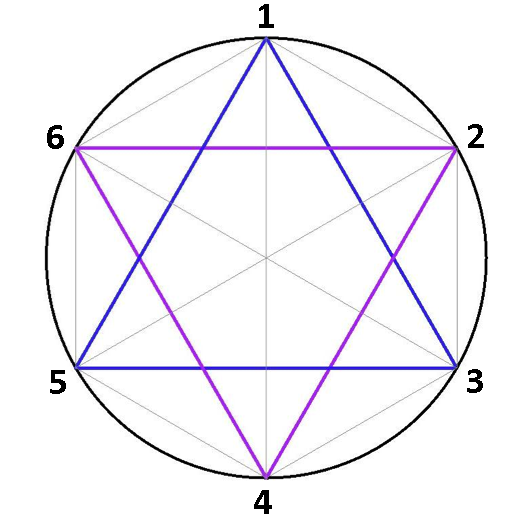
Cualquier simetría rígida de la imagen se puede describir mediante lo que sucede con los vértices; de manera que, por ejemplo, la secuencia 234561 representa la rotación de la imagen, en sentido contrario al de las manecillas del reloj, en un ángulo de 360/6=60 grados. La secuencia 345612 representa una rotación de 120 grados y la secuencia 432165 es el reflejo sobre el eje horizontal $x$.

Podemos definir la combinación de estas transformaciones mediante la simple aplicación de una secuencia tras otra: (234561)(432165) = (543216).

El conjunto de estas secuencias de dígitos forma un grupo: el grupo de isometrías del hexágono.

Si sólo nos interesan las rotaciones, entonces podemos considerar el grupo como:

$$G = \{\rho^i : 0\leq i \leq 5,\ \rho =(234561)\}$$

Este grupo es el grupo cíclico de orden 6, y se define mediante la relación:

$$\rho^6=1$$

Es un grupo muy importante en la definición de la recombinación de Sebastián, y da origen a la primera Cuántica que vimos en páginas anteriores.

13. Las simetrías y las recombinaciones son la fuente de las Cuánticas, pero también han desempeñado un papel fundamental en las matemáticas clásicas y modernas.

Uno se podría preguntar por qué los árboles crecen con un ángulo de 90 grados respecto del plano del suelo. Una vez más encontramos una cadena reduccionista que sería del siguiente tipo:

Matemáticas→ Biología→ Simetría (90 grados) → Adaptación → Belleza

El que un árbol crezca perpendicular al suelo, es desde luego la forma más simétrica en la cual podría crecer; la evolución darwiniana logró que esta simetría avanzara sigilosamente desde las matemáticas hasta la cima de los árboles.

Los ángulos de 90 grados son importantes porque son el avatar geométrico de una simetría de orden cuatro:

$$\rho^4=1$$

Girar la siguiente imagen cuatro veces, ciertamente es como no hacer nada:

Uno de los más bellos teoremas de las matemáticas es resultado de la unión entre esta simetría y una recombinación: el Teorema de Pitágoras:

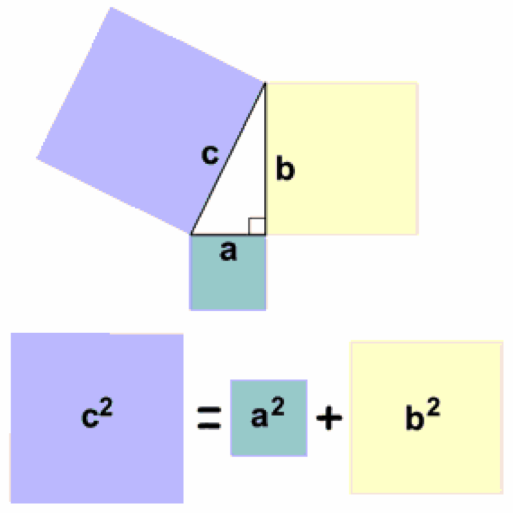
Su demostración es un bellísimo ejemplo de recombinación:

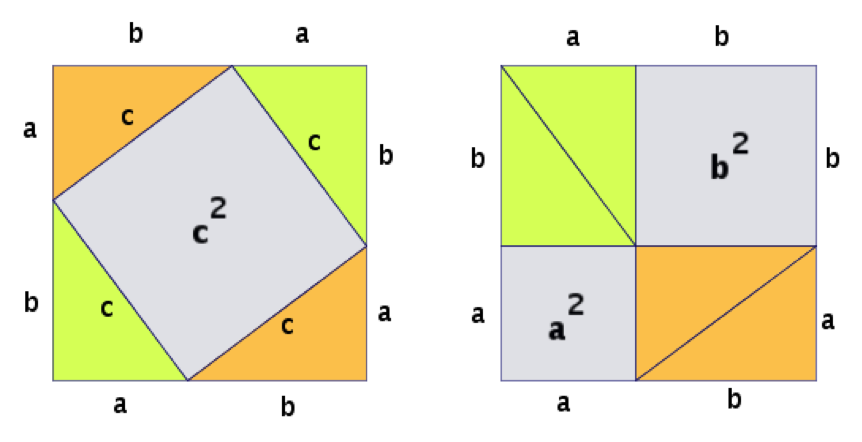
14. En la geometría, las simetrías de grupo poseen tanta relevancia que Félix Klein, en su “Erlanger Programm” [20]F.Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen Erlangen, 1872, reimpreso con notas adicionales en Mathematische Annalen 39 (1893): 257-278., propuso reducir la totalidad de la geometría a la teoría de grupos. Hasta el día de hoy, esta idea ha ejercido una gran influencia en las matemáticas.

15. El proceso fundamental de Sebastián es lo que hemos denominado la recombinación de Sebastián, tal como se representa a continuación:

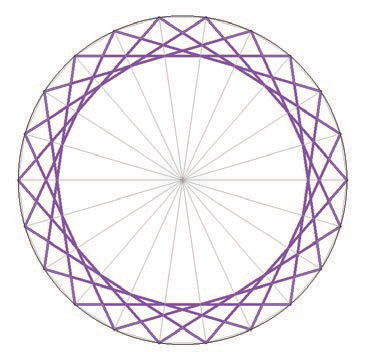
Exploremos brevemente algunas variaciones en el proceso general de recombinación utilizado por Sebastián. Consideremos un conjunto de $2k$ puntos, enumerados en el sentido de las manecillas del reloj e igualmente distribuidos en el círculo: los matemáticos se refieren a estos puntos como raíces $2k$-ésimas de la unidad, o simplemente como soluciones de la ecuación algebraica en coeficientes complejos:

$$x^{2k}-1=0$$

Formamos un polígono regular conectado mediante la unión de 2 puntos que se encuentren a una distancia fija $m$ (mod $2k$), donde $m$ y $2k$ son primos entre sí. Luego Sebastián gira el polígono alrededor del eje vertical (pasando a través del centro), para obtener algunas de sus Cuánticas más intrigantes. El siguiente ejemplo es el caso de $k=11$ y $m=5$.

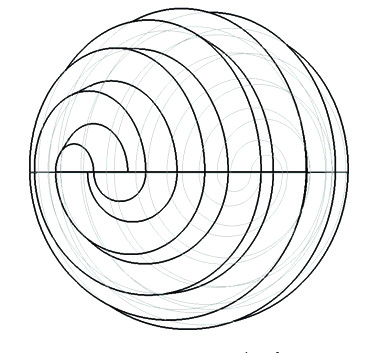
Después de una recombinación, obtiene lo siguiente:

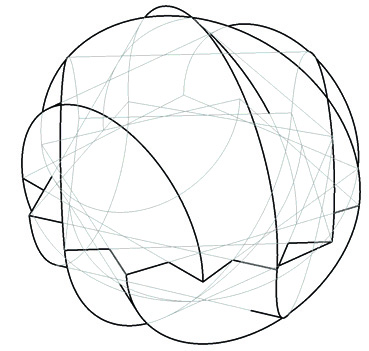
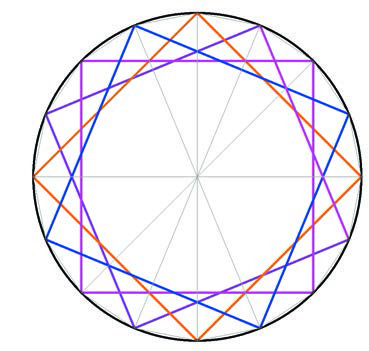
En otro conjunto de Cuánticas, Sebastián decide girar cada polígono inscrito en el círculo alrededor de varios ejes distintos e independientes. Esto puede considerarse como un modelo artístico de objetos con dimensiones más elevadas (pero diferente al Cubismo). En la figura que aparece a continuación, se muestra un modelo de tres dimensiones; el color en la figura podría de hecho interpretarse como una cuarta coordenada (aunque no en el sentido canónico); con ello se rompe una de las simetrías, exactamente en la misma forma en la que se rompe al ponerle color a la escultura:

16. Las simetrías también desempeñan un papel central en la física clásica y en la física cuántica. La misma ley de la conservación de la energía y muchas otras leyes de conservación, se pueden entender como casos de simetría en la física.

Emmy Noether (1882-1935) fue una de las más grandes matemáticas del siglo XX. Su trabajo es fundamental en el álgebra, la teoría de grupos y la física.

El primer teorema de Noether en la física matemática afirma que cualquier simetría en la acción de un sistema físico posee una correspondiente ley de conservación, dejando una cantidad física invariable en el tiempo [21]Emmy Noether, Invariante Variationsprobleme, Nachrichten von der Königliche Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse (1918): 235-257.. Este resultado fundamental iguala a la simetría con la conservación.

Lo que resulta aún más sorprendente es que el teorema sigue siendo válido en la física cuántica: de hecho, seguimos teniendo las identidades de Ward-Takahashi [22]John Clive Ward, An Identity in Quantum Electrodynamics, Physical Review 78 (1950): 182; Yasushi Takahashi, Nuovo Cimento, Ser. 10, 6 (1957): 370..

17. En la mecánica cuántica, hay muchos conceptos que desafían la intuición clásica: partículas que son ondas; sumas de todas las posibles narraciones de un suceso; Dios jugando a los dados y las probabilidades como único resultado. En palabras de Richard Feynman, uno de los padres de la teoría cuántica y ganador del premio Nobel:

Hubo un tiempo en el que los periódicos decían que sólo doce hombres entendían la teoría de la relatividad. Yo no creo que dicho tiempo haya existido jamás. Pudo haber un tiempo en el que un solo hombre la entendía, porque era la única persona que la había planteado, antes de escribir su artículo. Pero una vez que la gente leyó el artículo, seguramente más de doce personas entendieron la teoría de la relatividad de una u otra manera. En cambio, creo que puedo afirmar con certeza que nadie entiende la mecánica cuántica [23]H. Henry Stroke, ed., The Physical Review: The First Hundred Years: A Selection of Seminal Papers and Commentaries/Book and CD-ROM, New York, Springer-Verlag, 1995..

O en palabras de otro ganador del premio Nobel, el físico danés Neil Bohr:

Cualquiera que no esté impactado con la teoría cuántica, quiere decir que no la ha entendido [24]Nirvaldo J. Tro, Chemistry in Focus: A Molecular View of Our World, Belmont (CA), Brooks/Cole, 2012, p. 72.

Sin embargo, hay principios de nuestra intuición diaria que siguen siendo ciertos incluso en las alturas de la abstracción del formalismo cuántico. Uno de estos principios es la simetría, que siempre se mantiene como fuerza unificadora, tanto en el teorema de Noether como en el centro de lo que creemos que existe: la materia. La materia se conserva, por lo que debe provenir de una simetría, o como diría Eugene Wigner: los estados cuánticos de una partícula elemental deben remitirse a las representaciones irreductibles del grupo de Poincaré [25]David J. Gross, Symmetry In Physics: Wigner's Legacy, Physics Today (December 1995): 48..

En el reino de la física cuántica, la simetría rige suprema.

18. Ahora vayamos de regreso a las Cuánticas de Sebastián: las recombinaciones.

En la obra de Poincaré leemos lo siguiente:

Es cierto que las combinaciones que se presentan a la mente en una especie de iluminación súbita, después de un prolongado periodo de trabajo inconsciente, por lo general son combinaciones útiles y fecundas que parecen ser el resultado de una primera selección...

Sólo algunas son armoniosas y, en consecuencia, a la vez útiles y bellas; éstas serán capaces de tocar la especial sensibilidad del geómetra... que, una vez estimulada, atraerá sobre ellas nuestra atención, dándoles la ocasión de llegar a ser conscientes... [26]Henri Poincaré, Science and Method, capítulo 3, Mathematical Discovery, London, T. Nelson, 1914, p. 58.

Las Cuánticas de Sebastián son una exploración de estos misterios por parte del artista: simétricas, pero sólo parcialmente; combinaciones llevadas a la consciencia después de un periodo prolongado de trabajo inconsciente y recombinadas en una lúcida exploración del espacio, del movimiento y del tiempo, que juega con la forma en la que las cosas encajan; reveladas como las matemáticas, para proporcionar un puente en el camino estético entre el arte y la ciencia.

Bibliografía

1. G. H. Hardy, A Mathematician's Apology, Cambridge [UK], The University Press, 1940.

2. Bertrand Russell, The Study of Mathematics, Philosophical Essays, London/New York, Longmans/Green, 1910, pp. 73-74.

3. Denis Dutton, A Darwinian Theory of Beauty, archivo en video, (2010, noviembre), tomado de: www.ted.com/talks/denis_dutton_a_darwinian_theory _of_beauty.html

4. Karl Grammer y Randy Thornhill, Human (Homo sapiens) Facial Attractiveness and Sexual Selection: The Role of Symmetry and Averageness, Journal of Comparative Psychology 108, no. 3 (1994): 233–242.

5. B. C. Jones, A. C. Little, I. S. Penton-Voak, B. P. Tiddeman, D. M. Burt y D. I. Perrett, Facial Symmetry and Judgements of Apparent Health Support for a “Good Genes” Explanation of the Attractiveness-Symmetry Relationship, Evolution and Human Behavior 22, no. 6 (2001): 417–429.

6. Daniel C. Dennett, Darwin's Dangerous Idea: Evolution and the Meanings of Life, New York, Simon and Schuster, 1996.

7. Eugene P. Wigner, The Unreasonable Effectiveness of Mathematics in the Natural Sciences, Communications on Pure and Applied Mathematics 13, no.1 (1960): 1–14.

8. Roger Penrose and N. David Mermin, The Emperor's New Mind: Concerning Computers, Minds, and the Laws of Physics, American Journal of Physics 58 (1990): 1214.

9. Catalogue of Brancusi Exhibition, New York, Wildenstein Gallery, 1926.

10. Catalogue of Brancusi Exhibition, New York, Brummer Gallery, 1926.

11. Constantin Brancusi quoted by Dorothy Dudley, Brancusi, Dial 82 (1927): 126.

12. William Byers, How Mathematicians Think: Using Ambiguity, Contradiction, and Paradox to Create Mathematics, Princeton, Princeton University Press, 2010.

13. Hermann Weyl, Symmetry, Princeton, Princeton University Press, 1952; Princeton Science Library reprint (1989).

14. Dagobert Frey, Zum Problem der Symmetrie in der bildenen Kunst, Studium Generale 2 (1949): 276.

15. Matthew M. Hurley, Daniel Clement Dennett y Reginald B. Adams, Inside Jokes: Using Humor to Reverse-Engineer the Mind, Cambridge (MA), MIT Press, 2011.

16. M. R. Cook, R. C. Gunning, and B. Fradd, Mathematicians: An Outer View of the Inner World, Princeton, Princeton University Press, 2009, p. 24.

17. Richard Dawkins, The Selfish Gene, New York, Oxford University Press, 1976.

18. Ivor Grattan-Guinness, ed. History and Philosophy of the Mathematical Sciences vol. 1, Baltimore, Johns Hopkins University Press, 2003.

19. H. S. M. Coxeter, Regular Polytopes, New York, Dover Publications, third edition, 1973, cf. Lewis Carroll, Through the Looking-Glass, and What Alice Found There, London, Macmillan and Company, 1871 [postdated on title page to 1872].

20. F.Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen Erlangen, 1872, reimpreso con notas adicionales en Mathematische Annalen 39 (1893): 257-278.

21. Emmy Noether, Invariante Variationsprobleme, Nachrichten von der Königliche Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse (1918): 235-257.

22. John Clive Ward, An Identity in Quantum Electrodynamics, Physical Review 78 (1950): 182; Yasushi Takahashi, Nuovo Cimento, Ser. 10, 6 (1957): 370.

23. H. Henry Stroke, ed., The Physical Review: The First Hundred Years: A Selection of Seminal Papers and Commentaries/Book and CD-ROM, New York, Springer-Verlag, 1995.

24. Nirvaldo J. Tro, Chemistry in Focus: A Molecular View of Our World, Belmont (CA), Brooks/Cole, 2012, p. 72.

25. David J. Gross, Symmetry In Physics: Wigner's Legacy, Physics Today (December 1995): 48.

26. Henri Poincaré, Science and Method, capítulo 3, Mathematical Discovery, London, T. Nelson, 1914, p. 58.